Hi!
I'm here to introduce a new series of contests on HackerEarth, Data Structures and Algorithms (DSA) coding challenge! In this series, you will have to solve 3 problems in 1.5 hours.
The problems are classic and educational as against being creative and challenging. So, if you're learning new things, don't miss the DSA contests. These contests are similar to Codeforces Educational rounds.
We have hard problems and easy problems in this contest. After the contest, don't forget to upsolve! This will help you a lot.
The next DSA contest is on September 14, 4 AM UTC.
Authors are Devarshi (devarshi09) Khanna, Prakash (forgotter) Jha, and, Aditya (aditya123garg) Garg. I'm the tester of the round.
GL & HF!











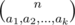 is odd and
is odd and 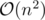 .
.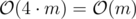 (Note that vector uses more memory than you need).
(Note that vector uses more memory than you need).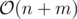 (for running dfs).
(for running dfs).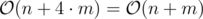 .
. 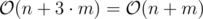 .
.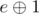 is its pair and it’s from
is its pair and it’s from 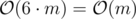 (Note that vector uses more memory than you need).
(Note that vector uses more memory than you need).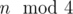 in a faster way.
in a faster way.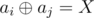 then
then 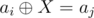 . Use trie.
. Use trie. is
is 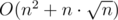 solution :O.
solution :O.
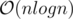 time (for all of the queries)?
time (for all of the queries)? .
. .
.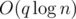 time (for
time (for 
