Over the years, many useful calendars for programming competitions have emerged like this, this and this. Some of these are still reliable, some are incomplete and some do not work anymore.
Today, in the opinion of many, HackerRank's calendar is the most complete one since you can find almost any competition, and its always up to date for a few months ahead. However, my own personal problem with it is that it's not sound. In other words, it has too many competitions that I usually do not have time to consider anymore, which ends up with a lot of noise on own personal Google calendar.
So in my attempts to create a more personalized calendar I found a bunch of feature requests for Google calendar to support filtering, or hide full day events, but these features are not supported, not even in the labs.
Then I found icalfilter.com which does exactly what I needed. I can give it the link to HackerRank's .ics and define some regexes for the events I want to know about like /srm/, /educational/, /div.*[12]/ and it will provide me with a link to a filtered .ics, which you can then add to Google calendar.
Here's a link to a filtered calendar (like the one I am using now, example above). It includes TopCoder SRMs, Codeforces Educational and regular Div 1 & 2 Rounds. You can use that as it is, or go ahead to icalfilter.com and create your own filtered version of any calendar you want!
Cheers and Happy Competing!








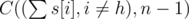 . We subtract one as Herr Wafa is guaranteed the spot, and the other
. We subtract one as Herr Wafa is guaranteed the spot, and the other 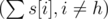 students.
students.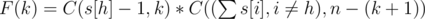 . Much like for the first set,
. Much like for the first set, 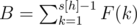 .
.

