Hi Everyone,
I'm delighted to announce that we will be hosting Indian Programming Camp (IPC) — 2020 edition online from November 20th — November 22nd. The camp has no charges and anyone can register and attend.
In the past, the IPC camp used to be conducted offline and was mainly targetted towards experienced IOI and ICPC aspirants. You can take a look at the IPC 2016 and IPC 2017 playlists to get an idea of the format.
This year, we are introducing three different tracks — Div3/Div2/Div1, catering to Beginner/Intermediate/Advanced programmers.
Event: Indian Programming Camp 2020
Dates: November 20th — November 22nd, 2020
Platform: YouTube and Unacademy
Tracks: Div1/Div2/Div3
Cost: Free of charge
Educators: Baba, EnEm, adurysk, sidhant, coder_pulkit_c, arjunarul, Riya Bansal, Sanket Singh
Registration Link: https://www.codechef.com/ipc/camp/2020
Note: Registered participants will be added to a discord server where live updates & discussions will be conducted during the camp, so please do register if you want to attend.
The exact schedule of the camp will be shared soon. Happy to answer any other open questions.
Thanks!
Tanuj
Update: We have sent reminder emails to all the registered participants. If you registered but haven't received an email, please let us know (either by comment or by email to [email protected])
The links to all classes in a track can be found here:
Div1: https://unacademy.com/a/i-p-c-advanced-track
Div2: https://unacademy.com/a/i-p-c-intermediate-track
Div3: https://unacademy.com/a/i-p-c-beginner-trackThe classes will also be streamed on Learn Competitive Programming with CodeChef youtube channel.
If you are able to create an account on Unacademy (everyone from India + some other countries), I would strongly suggest you to do so and enroll in the lectures on the unacademy platform since the classroom experience should be much better (ability to ask questions in chat, answer polls during the live class etc.).












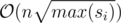
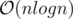
 .
.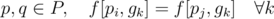 ). Any permutation of this group would be a valid bijection.
). Any permutation of this group would be a valid bijection.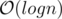 levels.
levels.
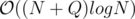

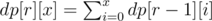
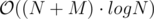
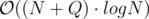
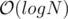 time by looking at it’s ancestors.
time by looking at it’s ancestors.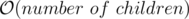 for each affected node and this number could be as large as
for each affected node and this number could be as large as 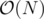 time in total !
time in total !

