TL 12 107676717 -- unordered_map<int, int> cnt (TL = 2s)
TL 18 107676732 -- unordered_map<int, int> cnt(n) (works 46ms on 12th test)
OK 107676952 -- sort (works 77ms and 66ms on 12th and 18th tests)
What's going on?) I have no access to tests and can not repeat this effect locally (both windows:g++, linux:g++)
UPD:
107679200 rehash(100 + gen() % 10000) gives OK in 670 ms, which is still too slow
107679288 rehash(100 + gen() % 10000) + reserve gives OK in 100 ms, which is strange but acceptable.
PS:
This comment says "anti-hash test". I also have only this idea.
This comment gives more precise answer.
In future of course i will just use my own hash-table with no such faults.
PPS:
Both constructor(x) and rehash(x) seems to set bucket_count to minimal prime $$$\ge$$$ x, so we can still use unordered_map in one of two following ways:
mt19937 gen(time(NULL));
unordered_map<int, int> cnt;
cnt.rehash(n + gen() % n);
mt19937 gen(time(NULL));
unordered_map<int, int> cnt(n + gen() % n);









 ? =)
? =)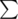 f[i,0]
f[i,0]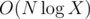 .
.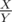 , where
, where 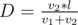 . Consider one candy. To eat it, he needs to get on the conveyor in any moment of the segment
. Consider one candy. To eat it, he needs to get on the conveyor in any moment of the segment  time.
time.
