As there is no tutorial of Codeforces Beta Round #5 in English, I have decided to write this one. Possibly, some ideas will be similar to ones, expressed in Russian tutorial made by SkidanovAlex, but I hope everybody will find some useful in this problem analysis too.
Both are implementation problems. The only difficult, many participants faced with - to read data correctly. It is recommended to use gets(s) or getline(cin, s) in C++, readLine() method of BufferedReader class in Java.
First of all, for each closing bracket in our string let's define 2 values:
Both d[j] and c[j] can be found with following algorithm, which uses stack.
This problem can be solved by careful case handling. Let's construct O(1) solution for it.
First of all, let's define 2 functions:
Having these functions, solution will be the following:
Let's reduce the problem from the circle to the straight line. Perform the following actions to do it:
General idea of the solution:
Consider there is a pair of hills, such that these hills are visible from each other. Let's define hill with lower height (if heights are equal - with lower position) as responsible for adding this pair to the answer.
From this point of view, hill x will adds to the answer 3 kinds of hills as his pair:
c[n] = 0;
for(int i = n - 1; i >= 0; --i) {
r[i] = i + 1;
while (r[i] < n && height[i] > height[r[i]]) r[i] = r[r[i]];
if (r[i] < n && height[i] == height[r[i]]) {
c[i] = c[r[i]] + 1;
r[i] = r[r[i]];
}
}
I am not going to prove here, that it works for the O(N) time, but believe it does :)
Pay attention, that r[x] is undefined for hills with maximum height and this algorithm will find r[x] = n for such hills.
Array l[x] can be found in a similar way.
Having l[x], r[x] and c[x], it's not so difficult to calculate the answer. We should just notice, that:
Problems A and B.
Both are implementation problems. The only difficult, many participants faced with - to read data correctly. It is recommended to use gets(s) or getline(cin, s) in C++, readLine() method of BufferedReader class in Java.
Problem C.
First of all, for each closing bracket in our string let's define 2 values:
- d[j] = position of corresponding open bracket, or -1 if closing bracket doesn't belong to any regular bracket sequence.
- c[j] = position of earliest opening bracket, such that substring s(c[j], j) (both boundaries are inclusive) is a regular bracket sequence. Let's consider c[j] to be -1 if closing bracket doesn't belong to any regular bracket sequence.
Both d[j] and c[j] can be found with following algorithm, which uses stack.
- Iterate through the characters of the string.
- If current character is opening bracket, put its position into the stack.
- If current character is closing bracket, there are 2 subcases:
- Stack is empty - this means that current closing bracket doesn't have corresponding open one. Hence, both d[j] and c[j] are equal to -1.
- Stack is not empty - we will have position of the corresponding open bracket on the top of the stack - let's put it to d[j] and remove this position from the stack. Now it is obvious, that c[j] is equal at least to d[j]. But probably, there is a better value for c[j]. To find this out, we just need to look at the position d[j] - 1. If there is a closing bracket at this position, and c[d[j] - 1] is not -1, than we have 2 regular bracket sequences s(c[d[j] - 1], d[j] - 1) and s(d[j], j), which can be concatenated into one larger regular bracket sequence. So we put c[j] to be c[d[j] - 1] for this case.
Problem D.
This problem can be solved by careful case handling. Let's construct O(1) solution for it.
First of all, let's define 2 functions:
- dist(speed, time) - calculates the distance will be covered in specified time, if car's current speed is speed. This function will not take car's speed limit into account. Also it assumes, that car is always driven with maximum acceleration a. It is obvious that required distance is equal to
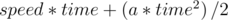 .
. - travelTime(distance, speed) - calculates the time, required to travel specified distance, if car have starting speed equal to speed. This function will also take care about car's speed limit.
We will have the following quadratic equation for time t: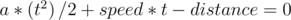 . This equation will have exactly 2 different roots. Using Viete's formulas it can be concluded, that one root of the equation is non-positive and other is non-negative. Let's define the larger root of the equation as tAll. It will be the answer, if there is no car's speed limit. To take the limit into account let's find the time, required to gain car's max speed. tMax = (v - speed) / a. If tMax ≥ tAll, function should just returns tAll as a result. Otherwise result is tMax hours to achieve car's maximal speed plus (distance - dist(speed, tMax)) / v hours to cover remaining distance.
. This equation will have exactly 2 different roots. Using Viete's formulas it can be concluded, that one root of the equation is non-positive and other is non-negative. Let's define the larger root of the equation as tAll. It will be the answer, if there is no car's speed limit. To take the limit into account let's find the time, required to gain car's max speed. tMax = (v - speed) / a. If tMax ≥ tAll, function should just returns tAll as a result. Otherwise result is tMax hours to achieve car's maximal speed plus (distance - dist(speed, tMax)) / v hours to cover remaining distance.
Having these functions, solution will be the following:
- If v ≤ w, answer is travelTime(l, 0).
- Calculate tw = w / a - time, required to gain speed w.
- Consider dw = dist(0, tw).
- If dw ≥ d, we will pass the point there sign is placed before we gain speed w. Answer for this case is travelTime(l, 0) as well.
- Otherwise, we will gain speed w before the sign. Let's consider segment of the road [dw, d]. We need to find out the best strategy to drive it. It is obvious, that we definitely should have speed w at the both ends of this segment. Also we know, that acceleration is equal to deceleration. Taking these facts into account we can see, that the speed in the optimal solution will be symmetrical with respect to the middle of the segment [dw, d]. Hence answer for this case will be tw + 2 * travelTime(0.5 * (d - dw), w) + travelTime(l - d, w).
Problem E.
Let's reduce the problem from the circle to the straight line. Perform the following actions to do it:
- Find the hill with the maximal height (if it is not unique, choose any).
- Rotate all the sequence in such a way that hill with maximal height goes first.
- For convenience, add one more hill with maximum height to the end of the sequence. (It will represent the first hill, which goes after the last in the circle order).
General idea of the solution:
Consider there is a pair of hills, such that these hills are visible from each other. Let's define hill with lower height (if heights are equal - with lower position) as responsible for adding this pair to the answer.
From this point of view, hill x will adds to the answer 3 kinds of hills as his pair:
- First hill to the left of the x, which is strictly higher than x. (Let's define its position as l[x])
- First hill to the right of the x, which is strictly higher than x. (Let's call this hill y and define it's position as r[x]).
- All hills that are as high as x and are located between x and y. (Let's define this count as c[x]).
c[n] = 0;
for(int i = n - 1; i >= 0; --i) {
r[i] = i + 1;
while (r[i] < n && height[i] > height[r[i]]) r[i] = r[r[i]];
if (r[i] < n && height[i] == height[r[i]]) {
c[i] = c[r[i]] + 1;
r[i] = r[r[i]];
}
}
I am not going to prove here, that it works for the O(N) time, but believe it does :)
Pay attention, that r[x] is undefined for hills with maximum height and this algorithm will find r[x] = n for such hills.
Array l[x] can be found in a similar way.
Having l[x], r[x] and c[x], it's not so difficult to calculate the answer. We should just notice, that:
- Each hill will add c[x] pairs to the answer.
- Each hill, lower than maximal, will also add 2 pairs (x, l[x]) and (x, r[x]) to the answer. The only corner case here is l[x] = 0 and r[x] = n, because (x, 0) and (x, n) is the same pair of hills in the original problem, where hills are circled.










