Today I tried to create a new problem on Polygon. After committing changes, I would like to create a problem package, but the following message appears:
PackageException: Failed on verification of the first test: Can't compile file: could not create dummy IR bfd: Memory exhausted collect2.exe: error: ld returned 1 exit status
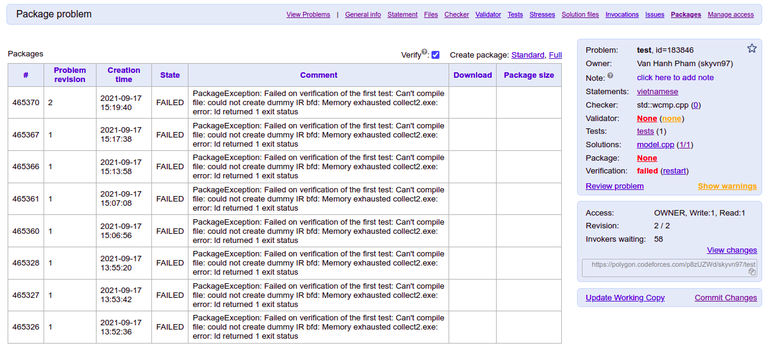
Has anyone encountered the same issue? Could you admins help me on this?
Have a good day everyone!











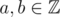 ,
, 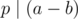 or
or 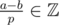 . It's quite easy to see that.
. It's quite easy to see that.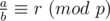 , for example:
, for example: 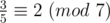 . What do they mean?
. What do they mean?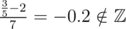 . But with the
. But with the 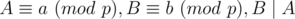 , we always have
, we always have 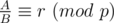 . Note that
. Note that 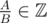 so we can use the definition for integers.
so we can use the definition for integers.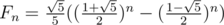
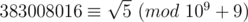
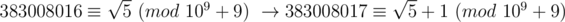 .
.