For each apple you just need to determine who like it. If Alexander likes apple, then he should eat it, if Artur likes the apple, then he should eat it. If they both like the apply anyone can eat the apple.
One should firstly recognize that the required string should be palindrome and each character of the string should be symmetric. All the symmetric characters are — AHIMOTUVWXY.
Firstly lets add to the answer all the persons, that didn't appear in the log messages. Then we should consider two cases:
1) If there is a person (with number i), that the first log message with him is in form - i. We will call such persons X-persons.
Consider all X-persons. Pick the one from them that has the last first occurrence in the sequence of messages. This person can be a leader, all others cannot be. Now we should check if the picked person is a leader or not. For that reason we will use the algorithm that is described below. This algorithm works fine only on special sequences of messages. So, we need to add all the X-persons to the beginning of the our list in the order they appear in input (in the resulting sequence the picked person should be the first).
2) There is no X-persons.
That case only the first person from the list can be a leader. Others cannot be. Check that person with the algorithm described below.
The Algorithm of check:
The algorithm is very simple. Just to iterate throughout the sequence of messages and maintain set-structure for the persons that are currently on the meeting. If we consider log-on message, add the person to the set, if we consider log-off message, erase the person from the set. Each time we perform an operation with set, we should check: either the set is empty or the leader is in set.
The most tricky cases are 33 and 34. Will look at them, the 33-th test:
4 4
+ 2
- 1
- 3
- 2
Here the leader can be only 4-th person. Others cannot be.
The 34-th test:
3 3
- 2
+ 1
+ 2
The answer for that test is only the 3-rd participant.
Lets construct an undirected graph, the vertices of the graph are the persons, there is an edge between two persons if there are claim of some person about these two persons. Now we can describe the problem on this graph. We need to find the number of such pairs of vertices that at least p edges are adjacent to them.
How to count such pairs. Just for each vertex v to calculate the number of vertices u such that d[v] + d[u] ≥ p, then we should consider all the adjacent vertices correctly. Iterate through all the edges and subtract such the vertices from the answer. Then iterate through adjacent vertices and add only such of them that is needed to be added.
Pay attention to multiple edges, they should be considered very carefully.
The solution consists of two parts.
1) Find the valid permutation.
Let's go through the given queries. Suppose the current query tells us that the number a is placed on b-th position. If we already met a then we are going to skip this query. Otherwise let's find the position of a in the sought permutation.
Suppose we already know that in the sought permutation the number a1 is on position b1, a2 is on position b2, ..., ak is on position bk (b1 < b2 < ... < bk). After every query the number from that query goes to the begging of the permutation, so all ai (1 ≤ i ≤ k) are already placed to the left of a before the current query. But some of these ai stood to the left of a in the sought permutation, and the other stood to the right of a, but went forward to the begging. Let's find the number of these numbers. In order to do this we should find such position p, that is not occupied by any of ai and p + x = b, where x is the number of such bi that bi > p.
We can do it by using the segment tree in the following manner. Let's store in the vertex of segment tree the number of already occupied positions on the correspond subsegment. Suppose we want to find p in the some subtree. Let's find the minimal position in the right subtree prg and the number of occupied positions xrg there. So if prg + xrg ≤ b then we should continue finding p in the right subtree. Otherwise we should decrease b by xrg and try to find p in the left subtree. When we find p we need to check that p + x = b. If this equation isn't correct then the answer is - 1.
2) Check that the sequence of the operations is correct.
Let's consider i-th query. Suppose it tells us that a is placed on position b. We should check whether it is correct. If we haven't already seen a in queries then this statement is correct because we checked it in the first part of the solution. Otherwise, let's find the such maximal j < i that it is given the position of a in j-th query. After j-th query a goes to the begging of the permutation and the other numbers can move it to the right. Let's find the number of such different numbers on the queries' segment [j + 1, i - 1]. We should get exactly b - 1.
Let's claim that we have ray and the infinite number of balls on it in this problem. The k-th ball is placed on the distance k·d from the begging of the ray. Let's note that in the answer must be the ball which is placed on the border of some cirlce. The second observation is the following. Let's consider any circle. The number of angles, on which we can rotate our ray so that any ball will be on the border of this cirlce, doesn't exceed 4 * r / d. Let's call these angles critical.
Let's put all critical angles from each circle to the array B and sort. After that let's consider every cirlce one-by-one. When we consider some cirlce we are going to find all critical angles and sort them. So the number of balls, which will be inside of the cirlce, will be the constant if we rotate our ray on every angle between the two neighbour critical angles. Let's find k — the number of these balls.
Let's create array C, where Ci is the answer value if we rotate the ray on the angle Bi. So after we find k and the positions of neighbour critical angles in B we need to perform add on the segment query in C. After we processed all critical angles of all circles the maximum in the C will be the answer.









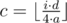 — how many laps he will run. Then he have already run
— how many laps he will run. Then he have already run 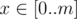 there is a zero on the
there is a zero on the 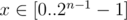 . In this case
. In this case 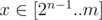 , find the maximum value of
, find the maximum value of 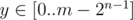 and add
and add 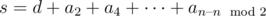 . But the minimal sum can be
. But the minimal sum can be 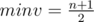 , and the maximal —
, and the maximal — 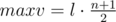 .
.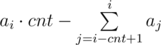 . If this value not greater than
. If this value not greater than 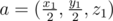 and normal to plane, containing the fixed face, which is directed out of interior of parallelepiped, that is
and normal to plane, containing the fixed face, which is directed out of interior of parallelepiped, that is 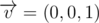 . Also take vector
. Also take vector 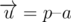 . If undirected angle between this vectors is less than
. If undirected angle between this vectors is less than 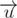 and
and 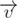 is strictly greater than zero, than that angle is fitting.
is strictly greater than zero, than that angle is fitting.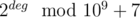 , because every cycle (1-vertex) increase the number of possible ways twice (you can go from one vertex to other by two ways in cycle).
, because every cycle (1-vertex) increase the number of possible ways twice (you can go from one vertex to other by two ways in cycle).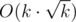 . Firstly, we show the main idea, than we show why solution has time complexity
. Firstly, we show the main idea, than we show why solution has time complexity 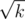 . Than diagonal will have length
. Than diagonal will have length 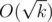 too. It means that we see
too. It means that we see 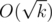 rows in each query and we do
rows in each query and we do 
