Hi. I am trying to solve this problem.
For convenience, I have summarised the problem statement below:
Problem Statement
We are tasked to arrange X Apples, Y Cherries and Z mangoes on a line, Compute the number of valid arrangements (modulo 1e9 + 7). All X + Y + Z fruits must be used in a single arrangement.
A valid arrangement is defined as an arrangement in which no two fruits of a similar kind are adjacent (no wraparound).
Constraints: 1 ≤ X, Y, Z ≤ 2e5
Time limit: 2s
Example
Example of a valid arrangement for X = 2, Y = 2, Z = 2 is:
Apple Orange Cherry Apple Orange Cherry
Example of a invalid arrangement for X = 2, Y = 2, Z = 2 is:
Apple Apple Orange Cherry Orange Cherry
My analysis
If the constraints were smaller, an obvious 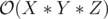 dynamic programming solution would suffice. However, the large constraints here seem to point towards a combinatorics solution (which I cannot figure out).
dynamic programming solution would suffice. However, the large constraints here seem to point towards a combinatorics solution (which I cannot figure out).
Could someone please advise me on how to solve this problem?









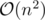 after a small optimization. Clearly, this will not pass the time limit.
after a small optimization. Clearly, this will not pass the time limit.
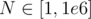 and each integer
and each integer 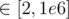 , sort the integers based on the lexicographical order of their prime factorization.
, sort the integers based on the lexicographical order of their prime factorization. blocks and sorting them in increasing order of left bound followed by increasing order of right bound. Time-complexity of this operation is
blocks and sorting them in increasing order of left bound followed by increasing order of right bound. Time-complexity of this operation is 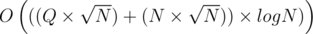 . This is because each query can only be in one block and block size is
. This is because each query can only be in one block and block size is 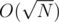 . Hence, the left pointer can only move by
. Hence, the left pointer can only move by  in total) and the right pointer moves by
in total) and the right pointer moves by  in total. Finally, each movement incurs an update operation in the BST which is
in total. Finally, each movement incurs an update operation in the BST which is 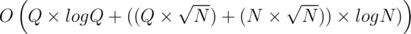 . However,
. However, 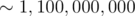 operations in the worst case (do note that the time-limit is only 4s). I tried coding this solution and as expected, it passed all but the last subtask (which uses the largest input).
operations in the worst case (do note that the time-limit is only 4s). I tried coding this solution and as expected, it passed all but the last subtask (which uses the largest input).
