A div2. Where do I Turn?
Let's consider cross product of vectors 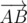 and
and 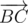 , which is equal to
, which is equal to 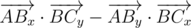 . Sign of cross product defines sign of a sine of oriented angle between vectors (because cross product is also equal to
. Sign of cross product defines sign of a sine of oriented angle between vectors (because cross product is also equal to 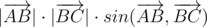 ), and that sign leads us to the correct answer.
), and that sign leads us to the correct answer.
If cross product is equal to zero, then A, B and C lay on the same straight line. So the answer is <>.
If cross product is more than zero, then answer is <>.
And, at last, if it's less than zero, the answer is <>.
Also you should notice that the value of cross product doesn't fit 32-bit type, so you have to use 64-bit type in order to avoid integer overflow.
B div2. Effective Approach
Let's assume that number t is on the indtth position in the original permutation. Then, obviously, during iterating from left to right this number will be found in indt comparisons, and during iterating from right to left — in n - indt + 1 comparisons. Let's declare additional array, in ith element of each there will be such number j, that aj = i. This array allows to process each query in O(1) using formulas referred above. Additional array is built in O(n) during iterating array a. So, the final complexity is O(n + m).
C div2 — A div1. Flying Saucer Segments.
Let Fn be the answer for the task, where n is equal to the amount of aliens. Let's assume, that we've solved problem for n - 1 aliens, i.e. we know the value of Fn - 1. Let's try to find value of Fn. Notice, that the most junior alien in rank will be able to leave the 3rd section, if and only if all other aliens are in the 1st section. So, now we know first Fn - 1 actions. Then the most junior alien may go to the 2nd section. To make for him entrance to the 1st section possible, it's necessary for all other aliens to return to the first one. So, Fn - 1 more actions are necessary. At last, after the most junior alien will go to the 1st section, Fn - 1 more actions are required for n - 1 other aliens to return to the 1st section from the 3rd. So, Fn = Fn - 1 + 1 + Fn - 1 + 1 + Fn - 1. It allows to count Fn using matrix exponentiation in O(log n), but we'll improve current solution. Let's add 1 to both parts of the equality and after elementary operations we'll have Fn = 3·(Fn - 1 + 1) - 1. Now it's easy to solve this reccurence: Fn = 3n - 1.
To count Fn quickly you should use binary power method. Solution's complexity — O(log n).
Don't forget that if 3n mod m = 0, answer is equal to m - 1, but not - 1.
And, in conclusion, notice that the task is equal to Hanoi Towers problem with a slight modification (it's impossible to move disks between one pair of rods).
D div2 — B div1. Naughty Stone Piles
Consider the following interpretation of the problem: stone piles are graph vertices. Operation "add pile a to pile b" changes to operation of suspencion of subtree of vertice b to vertice a. Numbers, written on vertices, — piles' sizes. Your task is to get such tree configuration, that each vertice has no more than k subtrees suspended to it, and sum of the products of numbers, written on vertices, and vertices' depth (where root's depth is 0) is minimal. In order to minimize the sum, at first, vertice with a larger number must be not deeply than vertice with smaller number (otherwise it's possible to change them and to get less sum), at second, each inner vertice, besides, maybe, one, has exactly k successors (the second condition is also proved using proof by contradiction). Now you are to learn how to calculate sum (described above) for this configuration quickly. In order do to it, let's sort piles' size array, and then let's do the following: at first, let's add to answer sum of sizes of piles from 1st to kth (in 0-indexed array, sorted in non-increasing order), multiplied by 1; then sum of sizes of next k2 piles, multiplied by 2; and so on till the end of array. In order to answer for the query about the sum of segment, precalculate sums of prefixes immediately after array sorting. Now in the case k > 1 we can find answer in O(log n). If you follow the same considerations for k = 1, answer for query will get O(n) operations that's why solution will get TL, if k is equal to 1 in most of the queries. So you should calculate the answer for k = 1 beforehand and memorize it, in order to response such queries in O(1).
Complexity — O(n · log n + q · log n).
E div2 — C div1. Anniversary
At first, let's prove the statement: GCD(Fn, Fm) = FGCD(n, m).
Let's express Fn + k using Fn and Fk. We'll get the formula: Fn + k = Fk·Fn + 1 + Fk - 1·Fn, which is easy to prove by induction.
Then use the derived formula and notice, that GCD(Fn + k, Fn) = GCD(Fk, Fn).
Now you are to notice an analogy with Euclidean algorithm and to understand, that we've got necessary equality for GCD of two Fibonacci numbers.
So, our current task is to find in the given set subset of k (or at least of k) elements with maximal possible GCD. To be exactly, to find this GCD.
Let the answer be equal to q. Then 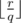 -
- 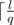 ⌉ + 1 ≥ k (1) must be true.
⌉ + 1 ≥ k (1) must be true.
Notice, that for each summand from left part of inequality O( 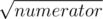 ) segments exist, in which its value is constant. Moreover, we can find all these segments and values in
) segments exist, in which its value is constant. Moreover, we can find all these segments and values in 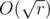 . To be more precise, we are intersted in such q, that in the point q - 1 value of at least one summand changes (obviously, increases). There are also
. To be more precise, we are intersted in such q, that in the point q - 1 value of at least one summand changes (obviously, increases). There are also 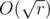 such values. Go over all of them and try to use each of them as the answer (i.e., check inequality (1) for each of them), and choose maximum from all satisfying numbers. The answer always exists, as q = 1 is true for any input.
such values. Go over all of them and try to use each of them as the answer (i.e., check inequality (1) for each of them), and choose maximum from all satisfying numbers. The answer always exists, as q = 1 is true for any input.
So, we've found index of required Fibonacci number. The number itself can be calculated by matrix exponentiation.
Complexity — 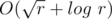 .
.
D div1. The table.
Let's get the required table. Act in the following way: find any row or column with negative sum and invert it. Notice, that sum of numbers in the entire table will always increase (at least, by 2). It can't increase permanently, because its maximal possible summary change is 200·n·m. So we'll get the required table anyway. It takes us not more than 100·n·m operations (applying of the spell), each of those is performed in O(n) or O(m). So, we've learned how to get required table in not more than ~ 1004 operations.
Now let's restore the answer. It's easy to understand that it will contain those rows and columns, which we've inverted odd times.
E div1. Noble Knight's Path
Solution 1
It's easy to guess that castles form a tree. Let's build heavy-light decomposition over it. Moreover, let's build persistent segment tree (with sum as the function) over each path. Tree's vertex will contain 0, if castle wasn't attacked by barbarians, and 1 otherwise.
Each knight's path should be divided into not more than two subpaths each of them lays on the path from one of the route's end to tree's root (just use lca in order to do it). Now let's solve the problem for each of the subpaths separately. We should sequentially process paths from heavy-light decomposition and single vertices, which lay on subpath. We are going to count the amount of vertices, which was not visited since year y + 1 up to the current year, i.e. (in the case of a path of the decomposition) such vertices, that the difference between values in the current version of persistent segment tree and in the version corresponding to year y (use binary search to find required version in the list of versions) is equal to zero (in case with single vertice it's enough to remember time when vertice was visited). As soon as the amount of appropriate vertices become not less than k, we should simultaneously walk down in two tree's versions in order to get the answer.
If the kth vertex isn't found on the first subpath, you should pay attention on the fact, that as we always go from down to up, we should accurately recalculate required vertex's number, in order to know it's position in the second subpath from down to up.
Complexity: O(m·log2 n) — in each query of the first type it can be necessary to update some segment tree, this action takes O(log n) operations; in each query of the second type there are O(log n) decomposition's paths, each of them is processed in O(log n) (firstly, binary search through versions' list, then query to the tree/walking down).
Solution 2
Let's go round the tree using dfs. When we enter the vertex and when we leave it let's put down vertex's number in the additional array (you can find out that this list has something same with regular brackets sequence). Assign 0 as the second number to all elements of the array. Then build persistent segment tree on the described array.
Now, when the first event happens, we'll assign + 1 to the second number in position of the first occurence of a castle's number, and - 1 to a position of the last one.
In order to answer for the second query, just notice, that we should count sum of the second numbers assigned to positions between first occurences of the vertices a and b in the array described above for finding the amount of visited vertices in the path connecting them.
Now on each of the paths separately start binary search for an answer — position of required castle. For the answer's check use the idea from the previous paragraph.
Complexity: O(m·log2 n) — in each query of the first type it can be necessary to update some segment tree, this action takes O(log n) operations; in each query of the second type there are O(log n) iterations of binary search on answer, each of iterations takes O(log n) operations.










