Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: Reyna
Writer: PrinceOfPersia
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: PrinceOfPersia
Writer: Reyna
Writer: PrinceOfPersia
I'm honored to announce that Codeforces round #459 is going to take place on January 29th and Reyna and I are the problemsetters of this round.
I'd like to thank keyvankhademi, AlexFetisov, winger, Belonogov, cyand1317 and demon1999, AnPelec for testing, KAN for coordinating the round and MikeMirzayanov for the great Codeforces and Polygon platforms.
The main characters of the round are Stranger Things characters.

The scoring distribution will be announced soon.
Good luck and have fun.
UPD0: The round is over, we hope you enjoyed it. Editorial will be posted soon.
UPD1: System testing is over, congratulations to the winners.
Div.1 winners are:
And Div.2 winners are:
The editorial will be posted in a bit.
UPD2: Here's the editorial. Also please help me and Reyna do better next time by filling out this form.
Happy new year people!
New year has always been special in competitive programming community, especially in Codeforces. We see different kinds of magic every year in Codeforces, and we're so grateful for them; thank you MikeMirzayanov. But, what if we too could show people some magic?
I was talking to one of my friends the other day, about competitive programming resources, and he reminded me that MAXimal is one the greatest resources for studying algorithms and data structures, however, it's not available to everyone since it's in Russian only. Of course, one could use google translate and try to understand it, but we all know even if it works, it's going to take a lot of time. So I had an idea! What if we translate all the articles in e-maxx to English? Of course, this isn't a job for one person, so I coudln't do it alone. And then, it crossed my mind... Crowd-sourcing! Everyone can contribute! Not only Russian speakers, but also others can use google translate for help. We're going to translate e-max together!
So I started today and spent the whole January 1st writing a website that's going to be a competitive programming resource available to everyone, in English (and later on, maybe even in other languages!). I called it AlgoBase.
You can register at AlgoBase and submit the articles you've translated. For now, we're only going to translate the "algo" section of e-maxx. The deadline to submit your translated articles is February 14th. Avoid altering the materials and translate them as they are. After the deadline, the best translated version of each article (chosen by votes) are going to be published (with the name of their translator) on AlgoBase.
To make it more interesting, two published articles (on AlgoBase) are going to be chosen randomly and their translators (more specifically, their usernames) are going to be the heroes of my CodeForces round (my next round after articles are published). And also, two other published articles are going to be chosen randomly and their translators will get AlgoBase T-Shirts. The selection is between articles, so the more articles you translate, the more chance you'll have at winning ;)
Happy translating!
TODO: Soon there will be a list of submitted translations available so that we know what articles have been translated and etc. Also it's possible that we add more prizes if more people participate!
UPD: Apparently there's a project named e-maxx-eng with the goal of translating e-maxx. But there are a lot of algorithms on e-maxx and only some in this project. But still, some pages are already translated. Therefore, the pages that are translated and present in e-maxx-eng are NOT ACCEPTED.
IOI 2017 is finally here and participants are arriving today. Here is IOI 2017 telegram group (since facebook is filtered in Iran). Join and enjoy.
As I promised, top IOI 2017 participant in each division in round #406 will be rewarded with special Persian souvenirs. That means matthew99 and xumingkuan (go China!). So hit me up you two.
Good luck and have fun!
Here's the git repository containing source codes for problems of this contest.








Don't hesitate to ask if you have any question/suggestion.
UPD: Git repo was not completely public, it is now. You can clone it or you can browse codes in "Repository" section.
Hello Codeforces, and happy Nowruz.
It's an honor to announce you that Codeforces Round #406 is going to take place on March 23rd.
I'm the writer of this round and it is gonna be my 6th CF contest (there are still plenty coming...). There are 5 problems and you'll have 120 minutes to solve them.
I'd like to thank keyvankhademi and waterfalls for testing this round, netman and KAN for helping me prepare this round and MikeMirzayanov for awesome platforms of Codeforces and Polygon.
The main characters of this round are going to be Rick and Morty!!!

Scoring will be posted soon.
Problems are sorted by their expected difficulty, but I strictly recommend you to read all the problems.
GL & HF!
P.S: Top IOI 2017 participant in each division (only with handle present in the future IOI handle list) will be rewarded with special Persian souvenirs in Tehran.
UPD: Scoring distribution is: 500, 1000, 1750, 2000, 2500 for Div.2 and 750, 1000, 1500, 2000, 2500 for Div.1
UPD: Editorial is out!
UPD: System test is over, congratulations to the winners.
Div.1 winners are:
Div.2 winners are:
See you next time ;)
Here are the solutions to all problems.
Just alternatively print "I hate that" and "I love that", and in the last level change "that" to "it".

Time Complexity: 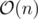
First of all, instead of cycles, imagine we have bamboos (paths). A valid move in the game is now taking a path and deleting an edge from it (to form two new paths). So, every player in his move can delete an edge in the graph (with components equal to paths). So, no matter how they play, winner is always determined by the parity of number of edges (because it decreases by 1 each time). Second player wins if and only if the number of edges is even. At first it's even (0). In a query that adds a cycle (bamboo) with an odd number of vertices, parity and so winner won't change. When a bamboo with even number of vertices (and so odd number of edges) is added, parity and so the winner will change.

Time Complexity: 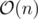
Consider a queue e for every application and also a queue Q for the notification bar. When an event of the first type happens, increase the number of unread notifications by 1 and push pair (i, x) to Q where i is the index of this event among events of the first type, and also push number i to queue e[x].
When a second type event happens, mark all numbers in queue e[x] and clear this queue (also decreese the number of unread notifications by the number of elements in this queue before clearing).

When a third type query happens, do the following:
while Q is not empty and Q.front().first <= t:
i = Q.front().first
x = Q.front().second
Q.pop()
if mark[i] is false:
mark[i] = true
e[v].pop()
ans = ans - 1 // it always contains the number of unread notifications
But in C++ set works much faster than queue!
Time Complexity: 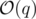
Reduction to TSP is easy. We need the shortest Hamiltonian path from s to e. Consider the optimal answer. Its graph is a directed path. Consider the induced graph on first i chairs. In this subgraph, there are some components. Each components forms a directed path. Among these paths, there are 3 types of paths:

There are at most 1 paths of types 2 and 3 (note that a path with beginning s and ending e can only exist when all chairs are in the subgraph. i.e. induced subgraph on all vertices).
This gives us a dp approach: dp[i][j][k][l] is the answer for when in induced subgraph on the first i vertices there are j components of type 1, k of type 2 and l of type 3. Please note that it contains some informations more than just the answer. For example we count d[i] or - x[i] when we add i to the dp, not j (in the problem statement, when i < j). Updating it requires considering all four ways of incoming and outgoing edges to the last vertex i (4 ways, because each edge has 2 ways, left or right). You may think its code will be hard, but definitely easier than code of B.
Time Complexity: 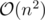
Build a graph. Assume a vertex for each clause. For every variable that appears twice in the clauses, add an edge between clauses it appears in (variables that appear once are corner cases). Every vertex in this graph has degree at most two. So, every component is either a cycle or a path. We want to solve the problem for a path component. Every edge either appear the same in its endpoints or appears differently. Denote a dp to count the answer. dp[i][j] is the number of ways to value the edges till i - th vertex in the path so that the last clause(i's) value is j so far (j is either 0 or 1). Using the last edge to update dp[i][j] from dp[i - 1] is really easy in theory.

Counting the answer for a cycle is practically the same, just that we also need another dimension in our dp for the value of the first clause (then we convert it into a path). Handling variables that appear once (edges with one endpoint, this endpoint is always an endpoint of a path component) is also hard coding. And finally we need to merge the answers.
Time Complexity: 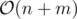
Assume r < b (if not, just swap the colors). Build a bipartite graph where every vertical line is a vertex in part X and every horizontal line is a vertex in part Y. Now every point(shield) is an edge (between the corresponding vertical and horizontal lines it lies on). We write 1 on an edge if we want to color it in red and 0 if in blue (there may be more than one edge between two vertices). Each constraint says the difference between 0 and 1 edges connected to a certain vertex should be less than or equal to some value. For every vertex, only the constraint with smallest value matters (if there's no constraint on this vertex, we'll add one with di = number of edges connected to i).
Consider vertex i. Assume there are qi edges connected to it and the constraint with smallest d on this vertex has dj = ei. Assume ri will be the number of red (with number 1 written on) edges connected to it at the end. With some algebra, you get that the constraint is fulfilled if and only if 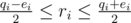 . Denote
. Denote 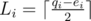 and
and 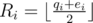 . So Li ≤ ri ≤ Ri. This gives us a L-R max-flow approach: aside these vertices, add a source S and a sink T. For every vertex v in part X, add an edge with minimum and maximum capacity Lv and Rv from S to v. For every vertex u in part Y, add an edge with minimum and maximum capacity Lu and Ru from u to T. And finally for every edge v - u from X to Y add an edge from v to u with capacity 1 (minimum capacity is 0).
. So Li ≤ ri ≤ Ri. This gives us a L-R max-flow approach: aside these vertices, add a source S and a sink T. For every vertex v in part X, add an edge with minimum and maximum capacity Lv and Rv from S to v. For every vertex u in part Y, add an edge with minimum and maximum capacity Lu and Ru from u to T. And finally for every edge v - u from X to Y add an edge from v to u with capacity 1 (minimum capacity is 0).

If there's no feasible flow in this network, answer is -1. Otherwise since r ≤ b, we want to maximize the number of red points, that is, maximizing total flow from S to T.
Since the edges in one layer (from X to Y) have unit capacities, Dinic's algorithm works in 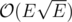 (Karzanov's theorem) and because
(Karzanov's theorem) and because 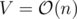 and
and 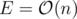 Dinic's algorithm works in
Dinic's algorithm works in 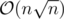 .
.
Time Complexity: 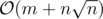
First, we're gonna solve the problem for when the given tree is a bamboo (path). For simplifying, assume vertices are numbered from left to right with 1, 2, .., n (it's an array). There are some events (appearing and vanishing). Sort these events in chronological order. At first (time - ∞) no suit is there. Consider a moment of time t. In time t, consider all available suits sorted in order of their positions. This gives us a vector f(t).

Lemma 1: If i and j are gonna be at the same location (and explode), there's a t such that i and j are both present in f(t) and in f(t) they're neighbours.
This is obvious since if at the moment before they explode there's another suit between them, i or j and that suit will explode (and i and j won't get to the same location).
Lemma 2: If i and j are present in f(t) and in time t, i has position less than j, then there's no time e > t such that in it i has position greater than j.
This hold because they move continuously and the moment they wanna pass by each other they explode.
So this gives us an approach: After sorting the events, process them one by one. consider ans is the best answer we've got so far (earliest explosion, initially ∞). Consider there's a set se that contains the current available suits at any time, compared by they positions (so comparing function for this set would be a little complicated, because we always want to compare the suits in the current time, i.e. the time when the current event happens). If at any moment of time, time of event to be processed is greater than or equal to ans, we break the loop. When processing events:
First of all, because current event's time is less than current ans, elements in se are still in increasing order of their position due to lemma 2 (because if two elements were gonna switch places, they would explode before this event and ans would be equal to their explosion time). There are two types of events:
Suit i appears. After updating the current moment of time (so se's comparing function can use it), we insert i into se. Then we check i with its two neighbours in se to update ans (check when i and its neighbours are gonna share the same position).
Suit i vanishes. After updating the current moment of time, we erase i from se and check its two previous neighbours (which are now neighbours to each other) and update ans by their explosion time.
This algorithm will always find the first explosion due to lemma 1 (because the suits that're gonna explode first are gonna be neighbours at some point).
This algorithm only works for bamboos. For the original problem, we'll use heavy-light decompositions. At first, we decompose the path of a suit into heavy-light sub-chains (like l sub-chains) and we replace this suit by l suits, each moving only within a subchain. Now, we solve the problem for each chain (which is a bamboo, and we know how to solve the problem for a bamboo). After replacing each suit, we'll get 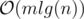 suits because
suits because 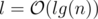 and we need an extra log for sorting events and using set, so the total time complexity is
and we need an extra log for sorting events and using set, so the total time complexity is 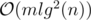 .
.
In implementation to avoid double and floating point bugs, we can use a pair of integers (real numbers).
Time Complexity (more precisely): 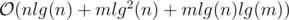
Hello ladies and gentlemen.
I'm honored to announce you that Codeforces Round #366(or should I say, IOI 2016 opening CF contest) is gonna take place on August 7th and I'm the writer. Please note that the timing is unusual.
As usual, there are 5 problems in each division and duration is 2 hours.
I want to thank LiTi for testing this round, GlebsHP for helping me prepare it and MikeMirzayanov for legendary and unique platforms of Polygon and CF.
The main characters of this round are The Avengers!
I wish you all Accepted solutions and Successful hacks.
Scoring will be posted soon.
Problems are sorted by their expected difficulty, but I strictly recommend you to read all the problems.
GL & HF!
P.S: Top IOI participant in each division (only with handle present in this list) will be rewarded with Persian souvenirs in Kazan.
UPD: Totally unrelated, but since the previous IOI group in telegram no longer exists, here's a new group!
UPD: Scoring is 500 — 1250 — 1250 — 2000 — 2500 in Div.1 and 500 — 1000 — 1500 — 2250 — 2250 in Div.2
UPD: I'm really sorry about the difficulty. System test is about to begin.
UPD: Editorial is out.
UPD: System test is over, congratulations to the winners.
Div.1 winners are:
Div.2 winners are:
Souvenir winners are lawrenceli from team USA and eXeP from team Finland (If that's not true write me in private).
Here is git repository to solutions of problems of this contest.
You should check two cases for YES:

Time Complexity: 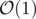
Nothing special, right? just find the position of letters . and e with string searching methods (like .find) and do the rest.

Time Complexity: 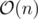
Do what problem wants from you. The only thing is to find the path between the two vertices (or LCA) in the tree. You can do this in 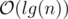 since the height of the tree is
since the height of the tree is 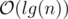 . You can keep edge weights in a map and get/set the value whenever you want. Here's a code for LCA:
. You can keep edge weights in a map and get/set the value whenever you want. Here's a code for LCA:
LCA(v, u):
while v != u:
if depth[v] < depth[u]:
swap(v, u)
v = v/2 // v/2 is parent of vertex v

Time Complexity: 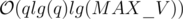
First of all starting_time of a vertex is the number of dfs calls before the dfs call of this vertex plus 1. Now suppose we want to find the answer for vertex v. For any vertex u that is not in subtree of v and is not an ancestor v, denote vertices x and y such that:

The probability that y occurs sooner than x in children[par[x]] after shuffling is 0.5. So the probability that starting_time[u] < starting_time[v] is 0.5. Also We know if u is ancestor of v this probability is 1 and if it's in subtree of v the probability is 0. That's why answer for v is equal to 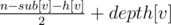 (depth is 1-based and sub[v] is the number of vertices in subtree of v including v itself). Because n - sub[v] - h[v] is the number of vertices like the first u (not in subtree of v and not an ancestor of v).
(depth is 1-based and sub[v] is the number of vertices in subtree of v including v itself). Because n - sub[v] - h[v] is the number of vertices like the first u (not in subtree of v and not an ancestor of v).
Thus answer is always either an integer or an integer and a half.
Time complexity: 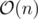
It gets tricky when the problem statement says p and q should be coprimes. A wise coder in this situation thinks of a formula to make sure this happens.
First of all let's solve the problem if we only want to find the fraction  . Suppose dp[i] is answer for swapping the cups i times. It's obvious that dp[1] = 0. For i > 0, obviously the desired cup shouldn't be in the middle in (i - 1) - th swap and with this condition the probability that after i - th swap comes to the middle is 0.5. That's why
. Suppose dp[i] is answer for swapping the cups i times. It's obvious that dp[1] = 0. For i > 0, obviously the desired cup shouldn't be in the middle in (i - 1) - th swap and with this condition the probability that after i - th swap comes to the middle is 0.5. That's why 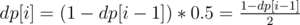 .
.

Some people may use matrix to find p and q using this dp (using pair of ints instead of floating point) but there's a risk that p and q are not coprimes, but fortunately or unfortunately they will be.
Using some algebra you can prove that:
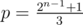 and q = 2n - 1.
and q = 2n - 1.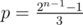 and q = 2n - 1.
and q = 2n - 1.You can confirm that in both cases p and q are coprimes (since p is odd and q is a power of 2).
The only thing left to handle is to find 2n (or 2n - 1) and parity. Finding parity is super easy. Also 2n = 2a1 × a2 × ... × ak = (...((2a1)a2)...)ak. So it can be calculated using binary exponential. Also dividing can be done using Fermat's little theorem.
Time complexity: O(klg(MAX_A)).
Build the prefix automaton of these strings (Aho-Corasick). In this automaton every state denotes a string which is prefix of one of given strings (and when we feed characters to it the current state is always the longest of these prefixes that is a suffix of the current string we have fed to it). Building this DFA can be done in various ways (fast and slow).
Suppose these automaton has N states (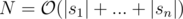 ) and state v has edges outgoing to states in vector neigh[v] (if we define our DFA as a directed graph). Suppose state number 1 is the initial state (denoting an empty string).
) and state v has edges outgoing to states in vector neigh[v] (if we define our DFA as a directed graph). Suppose state number 1 is the initial state (denoting an empty string).
If l was smaller we could use dp: suppose dp[l][v] is the maximum score of all strings with length equal to l ending in state v of our DFA when fed into it.
It's easy to show that dp[0][1] = 0 and dp[1][v] ≤ bv + dp[l + 1][u] for u in neigh[v] and calculating dps can be done using this (here bv is sum of a of all strings that are a suffix of string related to state v).

Now that l is large, let's use matrix exponential to calculate the dp. Now dp is not an array, but a column matrix. Finding a matrix to update the dp is not hard. Also we need to reform + and * operations. In matrix multiplying we should use + instead of * and max instead of + in normal multiplication.
Time complexity: 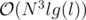 .
.
First of all, for each query of 1st type we can assume k = 1 (because we can perform this query k times, it doesn't differ).
Consider this problem: there are only queries of type 1.
For solving this problem we can use heavy-light decomposition. If for a vertex v of the tree we denote av as the weight of the lightest girl in it (∞ in case there is no girl in it), for each chain in HLD we need to perform two type of queries:
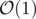 if we have the sorted vector of girls' weights for each vertex (and then we pop the last element from it and then current last element is the lightest girl, ∞ in case it becomes empty).
if we have the sorted vector of girls' weights for each vertex (and then we pop the last element from it and then current last element is the lightest girl, ∞ in case it becomes empty).
This can be done using a classic segment tree. In each node we only need a pair of integers: weight of lightest girl in interval of this node and the vertex she lives in (a pair<int, int>).
This works for this version of the problem. But for the original version we need an additional query type:
3. Increase weight of girls in a substring (consecutive subsequence) of this chain (a subchain) by k.
This can be done using the previous segment tree plus lazy propagation (an additional value in each node, type 3 queries to pass to children).
Now consider the original problem. Consider an specific chain: after each query of the first type on of the following happens to this chain:
When case 2 happens, v (query argument) belongs to this chain. And this can be done using the 3rd query of chains when we are processing a 2nd type query (effect the chain v belongs to).
When case 3 happens, v is an ancestor of the topmost vertex in this chain. So when processing 1st type query, we need to know sum of k for all 2nd type queries that their v is an ancestor of topmost chain in current chain we're checking. This can be done using a single segment/Fenwick tree (using starting-finishing time trick to convert tree to array).
So for each query of 1st type, we will check all chains on the path to find the lightest girl and delete her.
Time Complexity: 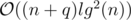
In the first thoughts you see that there's definitely a binary search needed (on r). Only problem is checking if there are such two points fulfilling conditions with radius r.
For each edge, we can shift it r units inside the polygon (parallel to this edge). The only points that can see the line coinciding the line on this edge are inside the half-plane on one side of this shifted line (side containing this edge). So problem is to partition these half-planes in two parts such that intersection of half-planes in each partition and the polygon (another n half-planes) is not empty. There are several algorithms for this propose:
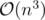 Algorithm:
Algorithm:

It's obvious that if intersection of some half-planes is not empty, then there's at least on point inside this intersection that is intersection of two of these lines (lines denoting these half-planes). The easiest algorithm is to pick any intersection of these 2n lines (n shifted half-planes and n edges of the polygon) like p that lies inside the polygon, delete any half-plane containing this point (intersection of deleted half-planes and polygon is not empty because it contains at least p) and check if the intersection of half-planes left and polygon is not empty (of course this part needs sorting half-planes and adds an additional log but we can sort the lines initially and use something like counting sort in this step).
Well, constant factor in this problem is too big and this algorithm will not fit into time limit. But this algorithm will be used to prove the faster algorithm:
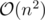 Algorithm:
Algorithm:
In the previous algorithm we checked if p can be in intersection of one part. Here's the thing:
Lemma 1: If p is inside intersection of two half-planes (p is not necessarily intersection of their lines) related to l - th and r - th edge (l < r) and two conditions below are fulfilled, then there's no partitioning that in it p is inside intersection of a part (and polygon):
Because if these two lines exist, they should be in the other part that doesn't contain p and if they are, intersection of them and polygon will be empty(proof is easy, homework assignment ;)).

This proves that if such partitioning is available that p is in intersection of one of them, then it belongs to an interval of edges(cyclic interval) and the rest are also an interval (so intersection of both intervals with polygon should be non-empty). Thus, we don't need p anymore. We only need intervals!
Result is, if such partitioning exists, there are integers l and r (1 ≤ l ≤ r ≤ n) such that intersection of half-planes related to l, l + 1, ..., r and polygon and also intersection of half-planes related to r + 1, r + 2, ..., n, 1, 2, ..., l - 1 and polygon are both non-empty.
This still gives an 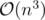 algorithm (checking every interval). But this lemma comes handy here:
algorithm (checking every interval). But this lemma comes handy here:
We call an interval(cyclic) good if intersection of lines related to them and polygon is non-empty.
Lemma 2: If an interval is good, then every subinterval of this interval is also good.
Proof is obvious.
That gives and idea:
Denote interval(l, r) is a set of integers such that:
(In other words it's a cyclic interval)
Also MOD(x) is:
(In other words it's modulo n for 1-based)
The only thing that matters for us for every l, is maximum len such that interval(l, MOD(l + len)) is good (because then all its subintervals are good).
If li is maximum len that interval(i, MOD(i + len)) is good, we can use 2-pointer to find values of l.
Lemma 3: lMOD(i + 1) ≥ li - 1.
Proof is obvious in result of lemma 2.
Here's a pseudo code:
check(r):
len = 0
for i = 1 to n:
while len < n and good(i, MOD(i+len)): // good(l, r) returns true iff interval(l, r) is good
len = len + 1
if len == 0:
return false // Obviously
if len == n:
return true // Barney and Lyanna can both stay in the same position
l[i] = len
for i = 1 to n:
if l[i] + l[MOD(i+l[i])] >= n:
return true
return false
good function can be implemented to work in 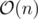 (with sorting as said before). And 2-pointer makes the calls to good to be
(with sorting as said before). And 2-pointer makes the calls to good to be 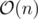 .
.
So the total complexity to check an specific r is 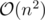 .
.
Time Complexity: 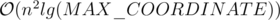
Feel free to comment and ask your questions.

— Hey, It's me again. Plain to see again...
— Oh crap, it's PrinceOfPersia again :|
I'm here to introduce you: Codeforces round 362. It's gonna take place on 196th day of 2016.
I'm the writer of this round. Not as always, there are 6 problems. I hope you enjoy.
I want to thank LiTi and Haghani for testing this round, danilka.pro and GlebsHP for helping me prepare the problems and MikeMirzayanov for legendary platforms of Codeforces and Polygon.
The main character of this round is Barney Stinson (high five ;)) and you're gonna help him with his problem.

I wish you all lots of Accepted solutions and hope to see no Skipped solutions ;)
Scoring will be posted soon.
GL & HF!
UPD: We decided that the contest has 6 problems (in each division, 4 shared). Duration will be announced as soon as we decide, but It's gonna be between 2 and 2:30 (inclusive).
UPD1: Duration is 2:15.
UPD2: Scoring is standard in both divisions: 500 — 1000 — 1500 — 2000 — 2500 — 3000
UPD3: Check out the editorial!
UPD4: System testing is over. Congratulations to the winners!
Div.1 Winners are:
Div.2 Winners are:
Idea is a simple greedy, buy needed meat for i - th day when it's cheapest among days 1, 2, ..., n.
So, the pseudo code below will work:
ans = 0
price = infinity
for i = 1 to n
price = min(price, p[i])
ans += price * a[i]

Time complexity: 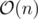
Find all prime divisors of n. Assume they are p1, p2, ..., pk (in 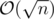 ). If answer is a, then we know that for each 1 ≤ i ≤ k, obviously a is not divisible by pi2 (and all greater powers of pi). So a ≤ p1 × p2 × ... × pk. And we know that p1 × p2 × ... × pk is itself lovely. So,answer is p1 × p2 × ... × pk
). If answer is a, then we know that for each 1 ≤ i ≤ k, obviously a is not divisible by pi2 (and all greater powers of pi). So a ≤ p1 × p2 × ... × pk. And we know that p1 × p2 × ... × pk is itself lovely. So,answer is p1 × p2 × ... × pk

Time complexity: 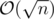
Problem is: you have to find the minimum number of k, such there is a sequence a1, a2, ..., ak with condition 2a1 + 2a2 + ... + 2ak = S = 2w1 + 2w2 + ... + 2w2. Obviously, minimum value of k is the number of set bits in binary representation of S (proof is easy, you can prove it as a practice :P).

Our only problem is how to count the number of set bits in binary representation of S? Building the binary representation of S as an array in 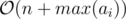 is easy:
is easy:
MAXN = 1000000 + log(1000000)
bit[0..MAXN] = {} // all equal to zero
ans = 0
for i = 1 to n
bit[w[i]] ++ // of course after this, some bits maybe greater than 1, we'll fix them below
for i = 0 to MAXN - 1
bit[i + 1] += bit[i]/2 // floor(bit[i]/2)
bit[i] %= 2 // bit[i] = bit[i] modulo 2
ans += bit[i] // if bit[i] = 0, then answer doesn't change, otherwise it'll increase by 1
Time complexity: 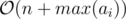
If we fix x and bix mod n, then problem will be solved (because we can then multiply it by the number of valid distinct values of 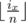 ).
).
For the problem above, let dp[i][j] be the number of valid subsequences of b where x = j and 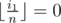 and
and 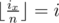 . Of course, for every i, dp[i][1] = 1. For calculating value of dp[i][j]:
. Of course, for every i, dp[i][1] = 1. For calculating value of dp[i][j]:
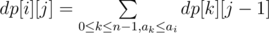
For this purpose, we can sort the array a and use two pointer:
if p0, p1, ...pn - 1 is a permutation of 0, ..., n - 1 where for each 0 ≤ t < n - 1, apt ≤ apt + 1:
for i = 0 to n-1
dp[i][1] = 1
for j = 2 to k
pointer = 0
sum = 0
for i = 0 to n-1
while pointer < n and a[p[pointer]] <= a[i]
sum = (sum + dp[p[pointer ++]][j - 1]) % MOD
dp[i][j] = sum

Now, if 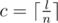 and x = l - 1 mod n, then answer equals to
and x = l - 1 mod n, then answer equals to 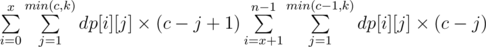 (there are c - j + 1 valid different values of
(there are c - j + 1 valid different values of 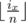 for the first group and c - j for the second group).
for the first group and c - j for the second group).
Time complexity: 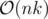
Solution is something like the fourth LCA approach discussed here.
For each 1 ≤ i ≤ n and 0 ≤ j ≤ lg(n), store the minimum 10 people in the path from city (vertex) i to its 2j - th parent in an array.
Now everything is needed is: how to merge the array of two paths? You can keep the these 10 values in the array in increasing order and for merging, use merge function which will work in 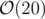 . And then delete the extra values (more than 10).
. And then delete the extra values (more than 10).
And do the same as described in the article for a query (just like the preprocess part).

Time complexity: 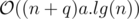
Run binary search on the answer (t). For checking if answer is less than or equal to x (check(x)):
First of all delete all edges with destructing time greater than x. Now, if there is more than one pair of edges with the same color connected to a vertex(because we can delete at most one of them), answer is "No".
Use 2-Sat. Consider a literal for each edge e (xe). If xe = TRUE, it means it should be destructed and it shouldn't otherwise. There are some conditions:
For each vertex v, if there is one (exactly one) pair of edges like i and j with the same color connected to v, then we should have the clause 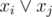 .
.
For each vertex v, if the edges connected to it are e1, e2, ..., ek, we should make sure that there is no pair (i, j) where 1 ≤ i < j ≤ k and xe1 = xe2 = True. The naive approach is to add a clause 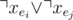 for each pair. But it's not efficient.
for each pair. But it's not efficient.

The efficient way tho satisfy the second condition is to use prefix or: adding k new literals p1, p2, ..., pk and for each j ≤ i, make sure 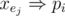 . To make sure about this, we can add two clauses for each pi:
. To make sure about this, we can add two clauses for each pi: 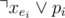 and
and 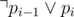 (the second one is only for i > 1).
(the second one is only for i > 1).
And the only thing left is to make sure 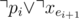 (there are no two
(there are no two TRUE edges).
This way the number of literals and clauses are 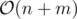 .
.
So, after binary search is over, we should run check(t) to get a sample matching.
Time complexity: 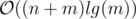 (but slow, because of the constant factor)
(but slow, because of the constant factor)
Lemma #1: If numbers b1, b2, ..., bk are k Kheshtaks of a1, ..., an, then  is a Kheshtak of a1, ..., an.
is a Kheshtak of a1, ..., an.
Proof: For each 1 ≤ i ≤ k, consider maski is a binary bitmask of length n and its j - th bit shows a subsequence of a1, ..., an (subset) with xor equal to bi.
So, xor of elements subsequence(subset) of a1, ..., an with bitmask equal to 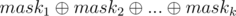 equals to
equals to  . So, it's a Kheshtak of this sequence.
. So, it's a Kheshtak of this sequence.
From this lemma, we can get another results: If all numbers b1, b2, ..., bk are k Kheshtaks of a1, ..., an, then every Kheshtak of b1, b2, ..., bk is a Kheshtak of a1, ..., an
Lemma #2: Score of sequence a1, a2, ..., an is equal to the score of sequence 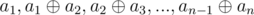 .
.
Proof: If we show the second sequence by b1, b2, ..., bn, then for each 1 ≤ i ≤ n:
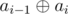

 each element from sequence b is a Kheshtak of sequence a and vise versa. So, due to the result of Lemma #1, each Kheshtak of sequence b is a Kheshtak of sequence a and vise versa. So:
each element from sequence b is a Kheshtak of sequence a and vise versa. So, due to the result of Lemma #1, each Kheshtak of sequence b is a Kheshtak of sequence a and vise versa. So:
 score(a1, ..., an) = score(b1, ..., bn)
score(a1, ..., an) = score(b1, ..., bn)

Back to original problem: denote another array b2, ..., bn where 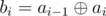 . Let's solve these two problems:
. Let's solve these two problems:
1- We have array a1, ..., an and q queries of two types:
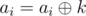
This problem can be solved easily with a simple segment tree using lazy propagation.
2- We have array b2, ..., bn and queries of two types:
This problem can be solved by a segment tree where in each node we have the basis of the substring of that node (node [l, r) has the basis of sequence bl, ..., br - 1).
This way we can insert to a basis vector v:
insert(x, v)
for a in v
if a & -a & x
x ^= a
if !x
return
for a in v
if x & -x & a
a ^= x
v.push(x)
But size of v will always be less than or equal to 32. For merging two nodes (of segment tree), we can insert the elements of one in another one.
For handling queries of two types, we act like this:
Type one: Call functions: upd(l, r, k), 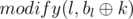 and
and 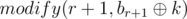 .
.
Type two: Let b = basis(l + 1, r). Call insert(al, b). And then print 2b.size() as the answer.
Time complexity: 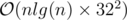 =
= 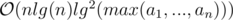
Use Aho-Corasick. Assume first of all we build the trie of our strings (function t). If t(v, c) ≠ - 1 it means that there is an edge in the trie outgoing from vertex v written c on it.
So, for building Aho-Corasick, consider f(v) = the vertex we go into, in case of failure (t(v, c) = - 1). i.e the deepest vertex (u), that v ≠ u and the path from root to u is a suffix of path from root to v. No we can build an automaton (Aho-Corasick), function g. For each i, do this (in the automaton):
cur = root
for c in s[i]
cur = g(cur, c)
And then push i in q[cur] (q is a vector, also we do this for cur = root).
end[cur].push(i) // end is also a vector, consisting of the indices of strings ending in vertex cur (state cur in automaton)
last[i] = cur // last[i] is the final state we get to from searching string s[i] in automaton g
Assume cnt(v, i) is the number of occurrences of number i in q[v]. Also, denote 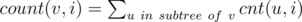 .
.
Build another tree. In this tree, for each i that is not root of the trie, let par[i] = f(i) (the vertex we go in the trie, in case of failure) and call it C-Tree.
So now, problem is on a tree. Operations are : Each query gives numbers l, r, k and you have to find the number 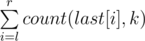 .
.

Act offline. If N = 105, then:
1. For each i such that 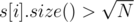 , collect queries (like struct) in a vector of queries query[i], then run
, collect queries (like struct) in a vector of queries query[i], then run dfs on the C-Tree and using a partial sum answer to all queries with k = i. There are at most  of these numbers, so it can be done in
of these numbers, so it can be done in 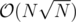 . After doing these, erase i from all q[1], q[1], ..., q[N].
. After doing these, erase i from all q[1], q[1], ..., q[N].
Code (in dfs) would be like this(on C-Tree):
partial_sum[n] = {}; // all 0
dfs(v, i){
cnt = 0;
for x in q[v]
if(x == i)
++ cnt;
for u in childern[v]
cnt += dfs(u);
for x in end[v]
partial_sum[x] += cnt;
return cnt;
}
calc(i){
dfs(root, i);
for i = 2 to n
partial_sum[i] += partial_sum[i-1]
for query u in query[i]
u.ans = partial_sum[u.r] - partial_sum[u.l - 1]
}
And we should just run calc(i) for each of them.
2. For each i such that 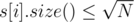 , collect queries (like struct) in a vector of queries query[i]. (each element of this vector have three integers in it: l, r and ans).
, collect queries (like struct) in a vector of queries query[i]. (each element of this vector have three integers in it: l, r and ans).
Consider this problem:
We have an array a of length N(initially all element equal to 0) and some queries of two types:
We know that number of queries of the first type is 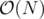 and from the second type is
and from the second type is 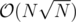 . Using Sqrt decomposition, we can solve this problem in
. Using Sqrt decomposition, we can solve this problem in 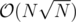 :
:
K = sqrt(N)
tot[K] = {}, a[N] = {} // this code is 0-based
increase(i, val)
while i < N and i % K > 0
a[i ++] += val
while i < K
tot[i/K] += val
i += K
sum(i)
return a[i] + tot[i/K]
Back to our problem now.
Then, just run dfs once on this C-Tree and act like this:
dfs(vertex v):
for i in end[v]
increase(i, 1)
for i in q[v]
for query u in query[i]
u.ans += sum(u.r) - sum(u.l - 1)
for u in children[v]
dfs(u)
for i in end[v]
increase(i, -1)
Then answer to a query q is q.ans.
Time complexity: 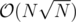

Hello Codeforces.
I'm honored to announce you, that Codeforces round #326 is gonna take place soon on Codeforces.
Writers are AmirMohammad Dehghan(PrinceOfPersia) and Ali Haghani(Haghani). There will be 6 problems in each division(4 problems are common) and you'll have 2 and a half hour to solve them. I hope you enjoy the problems.
I wanna thank Maxim Akhmedov(Zlobober) for his great helps in preparing this round, MikeMirzayanov for wonderful platforms of Codeforce and Polygon, Delinur for translating problem statements into Russian and MohammadReza Maleki(mruxim) and Ali Bahjati(LiTi) for their great advices (and LiTi again for some graphics).
This is my third round on Codeforces and not the last one, I hope.
This is the last round on Codeforces with Zlobober as coordinator. It was nice working with him. We had a lot of fun and interesting contests during his coordination. I just wanna say: Thank you Maxim for all your contribution to CodeForces community and good luck in the future. After I heard these news, my first guess for the next coordinator was I_love_Tanya_Romanova; But I don't know if CodeForces hires people from out of Russia or not.
The main character of this round is Duff, but you'll also have to help her friend, Malek!

I wish you all high ratings and lots of joy.
Scoring will be posted soon.
GL & HF!
Problems are sorted by the expected difficulty, but we strictly recommend you to read all the problems.
UPD: Scoring is: 750-1000-1500-2000-2500-3000 in Div.2 and 500-1000-1500-2000-2750-2750 in Div.1 .
UPD1: Editorial is published.
UPD2: System test is over. Congratulations to all winners.
Div.1 Winners are:
Div.2 Winners are:
Also congratulations to JoeyWheeler, the only one who solved problem Div.1 D.
Hello Codeforces.
Hunger games is a programming tournament.
For participating in this tournament, you should join as a participant in this group until the deadline. After the deadline you'll be able to join only as spectator.
In some time after the deadline (exact time will be published) tournament starts as a long contest in the group. At first, there will be some problems. Each day, organizers will add a non-negative number of problems to the contest. Also, at the end of each day, a non-negative number of participants from the bottom of the scoreboard will be deleted from the contest (to practice) and become spectators (not able to submit any more). Also, people that don't submit any code in first two-three (exact time will be published) days will become spectators.
Finally, there will be 20 peoples remaining at the end. We're still deciding about their prizes.
Duration of the tournament is not known yet. It will be published (it may be several weeks!).

Problems of the tournament may be copied (borrowed) from Codeforces or any online judge but we'll do our best to put new problems that we wrote ourselves. Also you may find a classic problem. To sum up, anything may happen in this tournament. Don't be shocked even if you see some April-fools-day-contest-problem-style problem.
Cheating and copying codes is forbidden(even copying your own old code) and you'll be disqualified from the the tournament if we catch you.
I think this is a good opportunity to practice and compete for all Codeforces members, because there will be hard and easy problems and good for everybody.
After the tournament ends, you'll be able to submit its problems in practice.
Currently, organizers team consists of AmirMohammad Dehghan(PrinceOfPersia) and Keyvan Khademi(keyvankhademi) but of course some more people will join.
Stay tuned, all future news will be published in the group blogs.
May the odds be ever in your favor.
UPD: Ali Asadi(aliasadiiii) joined our team.
UPD1: Tournament starts at August 12.
UPD2: Tournament is starting in about 3 hours. Don't forget to participate. Initially there will be 5 easy problems; But get ready, cause this shit's about to get heavy (problems will be added one by one during the tournament).
Team are not allowed.
You can read the news in the Memorial service.
Hello Codeforces !
Recently I've been busy with writing a Persian online judge. Result of my works is Codezilla. I'd like to thank matrix and HosseinYousefi for their helps (specially matrix).
Today I'm here to tell you that the first round is going to take place this Friday !

This contest will have 6 problems written by me(PrinceOfPersia) and duration is 3 hours. I recommend you all (Iranians) to participate in it. This is the first rated round of Codezilla.
Since Codezilla is in Persian (and problems there are in Persian), I created the group Codezilla (you can find it in "Groups" page, it's public) and I'll put all Codezilla rounds there as an English mirror that starts exactly 24 hours after the main round (for this round, it's on Saturday).
Good luck and Have fun !
UPD: Round started with 3 hours delay
UPD1: Codeforces mirror will start an August 2nd at 18:30 (Codeforces = Moscow timezone) in this group.
UPD2: Round started at 8. you can still take part.
Hello Codeforces.
Codeshark round #1 is going to take place on Codeshark this Friday morning at 2 PM (Tehran timezone). Codeshark website and the problem statements are in Persian, that's why I didn't put a link for time and date.
You can participate in the English version the next day (time) in Codeforces gym.
This contest will have 3 problems and each problem has some subtasks. Each subtask is a short answer algorithmic problem (like Projecteuler problems) and writers are aliasadiiii and me(PrinceOfPersia). Also, the duration is 4 hours.
I'd like to thank matrix (administrator of Codeshark) for his great helps.
Good luck and have fun.
UPD: There will be 12 subtasks (6, 3, 3).
UPD1: Schedule has changed (to 2 PM).
UPD2: Persian version is over.
Congratulations to the winners:
Interactive problems are problems in which solution talks to the judge. For example, 100553G - Gomoku. We don't see interactive problems much in ACM-ICPC style problems. Most of them are Olympiad style(IOI and CEOI). Unfortunately using interactive in Codeforces contests is not allowed, but you can see some of them in Gym. Also Polygon handles such problems(there's a checkbox Interactive in general info of the problem). When we don't wanna handle the judge manually, we should use a code named interactor to talk to code instead of a person. With testlib.h, we can write interactors as simple as checkers and validators.
In an interactive problem, you may use also a checker. To connect this programs together(generator, validator, solution, checker and interactor), you can use teslib input streams. An input stream, is a structure that reads data from a specific file using some pre-implemented methods. Input streams you can use with testlib.h:
inf: It's the input generated by generator or manually (In polygon, manual tests and output of generators, based on how the input file of the current testcase was generated).ouf: It's the output produced by the solution you're working on.ans: Output produced by your correct solution.Also, there's an input/output stream for interactive tasks named tout. It's a log file, you can write some information to it with the interactor and later, check the information written in it with the checker (and determine the verdict). For writing in it, you can use style of C++ cout, like tout << n << endl;. In the checker, you can read that information from ouf.
Methods you can use for input streams: Validator doc
In interactor, you read the information about the current testcase from inf, write what needs to be given to the solution you're checking and the correct solution using stdout (online), read the output produces by the solution you're checking using ouf (online), read the output produces by your correct solution using ans (online) and write log to tout if you want.
If at anytime, some with methods of input streams used in interactor goes wrong(fails), verdict will be Wrong Answer.
Also, you can determine the verdict in interactor. There are much useful methods in teslib you can use in interactors for assert-like checking, ensuring and determining the verdict. You can find them in checker docs (methods like quitf and ensuref).
You can also see possible verdicts in checker docs.
If verdict determined by interactor's ok, then it will be ensured by the checker (which uses tout/ouf) if there's any.
How to use interactor program ?
Simple:
Windows:
interactor.exe <Input_File> <Output_File> [<Answer_File> [<Result_File> [-appes]]],
Reads test from inf (mapped to args[1]), writes result to tout (mapped to argv[2],
can be judged by checker later), reads program output from ouf (mapped to stdin),
writes output to program via stdout (use cout, printf, etc).
Linux:
./interactor.out <Input_File> <Output_File> [<Answer_File> [<Result_File> [-appes]]],
Reads test from inf (mapped to args[1]), writes result to tout (mapped to argv[2],
can be judged by checker later), reads program output from ouf (mapped to stdin),
writes output to program via stdout (use cout, printf, etc).
I(judge) choose an integer in the interval [1, 109] and you should write a code to guess it. You can ask me at most 50 questions. In each question, you tell me a number in the interval [1, 109], and I tell you:
Sample interactor for this problem:
Note: Like checkers and validators and generator, you should first initialize your interactor with registerInteraction(argc, argv).
Please note that in this problem, we can determine the verdict without using the correct solution and ans because we don't care about it's product. But in some problems, we'll have to compare it with the product of the correct solution using ans.
int main(int argc, char ** argv){
registerInteraction(argc, argv);
int n = inf.readInt(); // chosen integer
cout.flush(); // to make sure output doesn't stuck in some buffer
int left = 50;
bool found = false;
while(left > 0 && !found){
left --;
int a = ouf.readInt(1, 1000000000); // the number you tell me
if(a < n)
cout << 0 << endl;
else if(a > n)
cout << 2 << endl;
else
cout << 1 << endl, found = true;
cout.flush();
}
if(!found)
quitf(_wa, "couldn't guess the number with 50 questions");
ouf.readEof();
quitf(_ok, "guessed the number with %d questions!", 50 - left);
}
Resources: Checkers, validators and my personal experience from reading one of MikeMirzayanov's interactors.
Consider characters of this string are number 0-based from left to right. If |s| is not a multiply of k, then answer is "NO". Otherwise, let 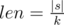 . Then answer is "Yes" if and only if for each i that 0 ≤ i < |s|, si = s(i / len) * len + len - 1 - (i%len) where a%b is the remainder of dividing a by b.
. Then answer is "Yes" if and only if for each i that 0 ≤ i < |s|, si = s(i / len) * len + len - 1 - (i%len) where a%b is the remainder of dividing a by b.

Time complexity: 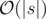 .
.
Consider this problem: We have a binary sequence s and want to find the maximum number of consecutive 1s in it. How to solve this? Easily:
ans = 0
cur = 0
for i = 1 to n:
if s[i] == 0
then cur = 0
else
cur = cur + 1
ans = max(ans, cur)

Finally, answer to this problem is ans. For each row r of the table, let ansr be the maximum number of consecutive 1s in it (we know how to calculate it in O(m) right ?). So after each query, update ansi in O(m) and then find max(ans1, ans2, ..., ansn) in O(n).
Time complexity: 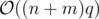
In this editorial, consider p = m, a = h1, a′ = a1, b = h2 and b′ = a2, x = x1, y = y1, X = x2 and Y = y2.
First of all, find the number of seconds it takes until height of Xaniar becomes a′ (starting from a) and call it q. Please note that q ≤ p and if we don't reach a′ after p seconds, then answer is - 1.
If after q seconds also height of Abol will become equal to b′ then answer if q.
Otherwise, find the height of Abdol after q seconds and call it e.
Then find the number of seconds it takes until height of Xaniar becomes a′ (starting from a′) and call it c. Please note that c ≤ p and if we don't reach a′ after p seconds, then answer is - 1.
if g(x) = Xx + Y, then find f(x) = g(g(...(g(x)))) (c times). It is really easy:
c = 1, d = 0
for i = 1 to c
c = (cX) % p
d = (dX + Y) % p
Then,
f(x)
return (cx + d) % p

Actually, if height of Abol is x then, after c seconds it will be f(x).
Then, starting from e, find the minimum number of steps of performing e = f(e) it takes to reach b′ and call it o. Please note that o ≤ p and if we don't reach b′ after p seconds, then answer is - 1.
Then answer is x + c × o.
Time Complexity: 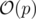
For each i, find the largest j that aj < ai and show it by li (if there is no such j, then li = 0).
Also, find the smallest j that aj < ai and show it by ri (if there is no such j, then ri = n + 1).
This can be done in O(n) with a stack. Pseudo code of the first part (second part is also like that) :
stack s // initially empty
for i = 1 to n
while s is not empty and a[s.top()] >= a[i]
do s.pop()
if s is empty
then l[i] = 0
otherwise
l[i] = s.top()
s.push(i)

Consider that you are asked to print n integers, ans1, ans2, ..., ansn. Obviously, ans1 ≥ ans2 ≥ ... ≥ ansn.
For each i, we know that ai can be minimum element in groups of size 1, 2, ..., ri - li - 1.
Se we need a data structure for us to do this:
We have array ans1, ans2, ..., ansn and all its elements are initially equal to 0. Also, n queries. Each query gives x, val and want us to perform ans1 = max(ans1, val), ans2 = max(ans2, val), ..., ansx = max(ansx, val). We want the final array.
This can be done in O(n) with a maximum partial sum (keeping maximum instead of sum), read here for more information about partial sum.
Time complexity: 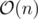 .
.
We define that a number x is good if and only if there is no y > 1 that y2 is a divisor of x.
Also, we define function f(x) as follow:
Consider x = p1a1 × p2a2 × ... × pkak where all pis are prime. Then, f(x) = a1 + a2 + ... + an.
Use simple inclusion. Consider all the primes from 1 to 5 × 105 are p1, p2, ..., pk.
So, after each query, if d(x) is the set of beers like i in the shelf that x is a divisor of ai, then number of pairs with gcd equal to 1 is: 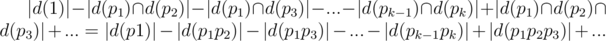
Consider good numbers from 1 to 5 × 105 are b1, b2, ..., bm. The above phrase can be written in some other way: |d(b1)| × ( - 1)f(b1) + |d(b2)| × ( - 1)f(b2) + ... + |d(bm)| × ( - 1)f(bm).
So, for each query if we can find all good numbers that ai is divisible by them in a fast way, we can solve the rest of the problem easily (for each good number x, we can store |d(x)| in an array and just update this array and update the answer).

Since all numbers are less than 2 × 3 × 5 × 7 × 11 × 13 × 17, then there are at most 6 primes divisible buy ai. With a simple preprocesses, we can find their maximum and so easily we can find these (at most 6) primes fast. If their amount is x, then there are exactly 2x good numbers that ai is divisible by them (power of each prime should be either 0 or 1).
So we can perform each query in O(26)
Time complexity: 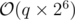 .
.
Consider a bipartite graph. In each part (we call them first and second part) there are L = 2 × 105 vertices numbered from 1 to L. For each point (x, y) add an edge between vertex number x from the first part and vertex number y from the second part.
In this problem, we want to color edges with two colors so that the difference between the number of blue edges connected to a vertex and the number of red edges connected to it be at most 1.
Doing such thing is always possible.
We prove this and solve the problem at the same time with induction on the number of edges :

If all vertices have even degree, then for each component there is an Eulerian circuit, find it and color the edges alternatively_ with blue and red. Because graph is bipartite, then our circuit is an even walk and so, the difference between the number of blue and red edges connected to a vertex will be 0.
Otherwise, if a vertex like v has odd degree, consider a vertex like u that there is and edge between v and u. Delete this edge and solve the problem for the rest of the edges (with the induction definition) and then add this edge and if the number of red edges connected to u is more than the blue ones, then color this edge with blue, otherwise with red.
You can handle this add/delete edge requests and find odd vertices with a simple set. So,
Time complexity: 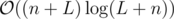
call(i, j) = match(sjinsi) which match(tins) is the number of occurrences of t in s.
Concatenate all strings together in order (an put null character between them) and call it string S. We know that 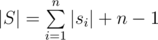 .
.
Consider N = 5 × 105. Consider Consider for each i, Sxisxi + 1...syi = si (xi + 1 = yi + 2).
Also, for i - th character of S which is not a null character, consider it belongs to swi.
Calculate the suffix array of S in 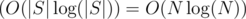 and show it by f1, f2, ..., f|S| (we show each suffix by the index of its beginning).
and show it by f1, f2, ..., f|S| (we show each suffix by the index of its beginning).
For each query, we want to know the number of occurrences of sk in Sxl...syr. For this propose, we can use this suffix array.
Consider that we show suffix of S starting from index x by S(x).
Also, for each i < |S|, calculate lcp(S(fi), S(fi + 1)) totally in 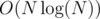 and show it by lci.
and show it by lci.

For each query, consider fi = xk, also find minimum number a and maximum number b (using binary search and sparse table on sequence lc) such that a ≤ i ≤ b and min(lca, lca + 1, ..., lci - 1) ≥ |sk| and min(lci, lci + 1, ..., lcb - 1) ≥ |sk|.
Finally answer of this query is the number of elements in wa, wa + 1, ..., wb that are in the interval [l, r].
This problem is just like KQUERY. You can read my offline approach for KQUERY here. It uses segment tree, but you can also use Fenwick instead of segment tree.
This wasn't my main approach. My main approach uses aho-corasick and a data structure I invented and named it C-Tree.
Time complexity: 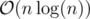
C++ Code by PrinceOfPersia (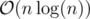 )
)
C++ Code by PrinceOfPersia (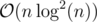 )
)
C++ Code by Haghani (Suffix array construction in 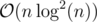 and the rest in
and the rest in 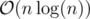 )
)

If there's any suggestion or error let me know.
Codeforces round #305 is gonna take place soon and I'm the writer.
After my previous contest that many people think it was a hard contest, I prepared an easy contest to cheer you up!
I want to thank Haghani for testing this round, Zlobober for help me prepare this round and his great advises, Delinur for translating problem statements into Russian, mruxim and Yasser Ahmadi Phoulady (Rasta) for their advises and ideas, HosseinYousefi for helping me choose legends and graphics and MikeMirzayanov for great Codeforces and Polygon platform and guys from Physics Olympiad that kept disturbing me while preparing this round.
This is my second official round and I hope you enjoy it.
The main character of this round is gonna be Mike (I didn't say MikeMirzayanov :D).

Also you'll meet Xaniar and Abol.
I wish you all Successful hacks and Accepted solutions and high ratings.
Scoring will be posted soon.
GL & HF!
UPD: Scoring is:
UPD2: Due to technical reasons we moved the round by 5 minutes.
UPD3: Contest has just ended. You can find the editorial here.
UPD4: System testing is done.
Congratulations to the winners, specially dreamoon_love_AA that got to his goal !
Div.1 winners:
Div.2 winners:
See you in the next rounds.
First of all check if n is one of the values 0, 10, 11, …, 19. Then, let’s have array x[] = {"", "", "twenty", "thirty", …, "ninety"} and y[] = {"", "one", …, "nine"}.

Let 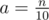 and b = n modulo 10.
and b = n modulo 10.
If n is not one of the values above, then if a = 0, print y[b], else if b = 0 print x[a] otherwise print x[a]-y[b].
Time complexity: O(1)
Another Code by PrinceOfPersia
Sol1: Consider n has x digits, f(i) = decimal representation of binary string i, m is a binary string of size x and its i - th digit is 0 if and only if the i - th digit of n is 4. Finally, answer equals to 21 + 22 + … + 2x - 1 + f(m) + 1.
Time complexity: O(log(n))

Sol2: Count the number of lucky numbers less than or equal to n using bitmask (assign a binary string to each lucky number by replacing 4s with 0 and 7s with 1).
Time complexity: O(2log(n))
Lemma: Sequence h1, h2, …, hn is (m, t) - Tavas-Eatable if and only if max(h1, h2, …, hn) ≤ t and h1 + h2 + … + hn ≤ m × t.
Proof: only if is obvious (if the sequence is Tavas-Eatable, then it fulfills the condition).
So we should prove that if the conditions are fulfilled, then the sequence is Tavas-Eatable.
Use induction on h1 + h2 + ... + hn. Induction definition: the lemma above is true for every sequence h with sum of elements at most k. So now we should prove it for h1 + h2 + ... + hn = k + 1. There are two cases:
1- There are at least m non-zero elements in the sequence. So, the number of elements equal to t is at most m (otherwise sum will exceed m × t). So, we decrease m maximum elements by 1. Maximum element will be at most t - 1 and sum will be at least m × t - m = m(t - 1). So according to the induction definition, the new sequence is (m, t - 1) - Tavas-Eatable, so h is (m, t) - Tavas-Eatable.
2- There are less than m non-zero elements in the sequence. We decrease them all by 1. Obviously, the new sequence has maximum element at most equal to t - 1 so its sum will be at most m(t - 1). So according to the induction definition, the new sequence is (m, t - 1) - Tavas-Eatable, so h is (m, t) - Tavas-Eatable.

For this problem, use binary search on r and use the fact that the sequence is non-decreasing and 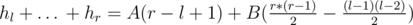 .
.
Time complexity: O(qlog(mt))
First of all you need to find uncovered positions in s (because rest of them will determine uniquely). If there is no parados in covered positions (a position should have more than one value), then the answer will be 0, otherwise it’s 26uncovered. To check this, you just need to check that no two consecutive matches in s have parados. So, for this purpose, you need to check if a prefix of t is equal to one of its suffixes in O(1). You can easily check this with prefix function (or Z function).

Time complexity: O(n + m)
For each competitor put the point 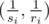 in the Cartesian plane. So, the time a competitor finishes the match is
in the Cartesian plane. So, the time a competitor finishes the match is 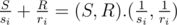 .
.
Determine their convex hull(with maximum number of points. i.e it doesn’t matter to have π radians angle). Let L be the leftmost point on this convex hull (if there are more than one, choose the one with minimum y component). Similarly, let D be the point with minimum y component on this convex hull (if there are more than one, consider the leftmost).
Proof: 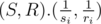 is the scalar product that is smaller if the point
is the scalar product that is smaller if the point 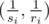 is farther in the direction of (S, R). It's obvious that the farthest points in some direction among the given set lie on a convex hull. (S, R) can get any value that is vector in first quadrant. So we need the points on the convex hull that we actually calculate (also we know that the points on the right or top of the convex hull, are not in the answer, because they're always losers).
is farther in the direction of (S, R). It's obvious that the farthest points in some direction among the given set lie on a convex hull. (S, R) can get any value that is vector in first quadrant. So we need the points on the convex hull that we actually calculate (also we know that the points on the right or top of the convex hull, are not in the answer, because they're always losers).

It’s easy to see that the answer is the points on the path from D to L on the convex hull (bottom-left arc). i.e the bottom-left part of the convex hull.
Time complexity: O(nlog(n))
In this problem, we recommend you to use integers. How ? Look at the code below
In this code, function CROSS returns  (it's from order of 1016, so there won't be any overflows.)
(it's from order of 1016, so there won't be any overflows.)
In double version, you should have a very small epsilon.
Code of double version by PrinceOfPersia
Another Code With Lower Envelope of Lines by Haghani
For each vertex v, put a point (dis(s, v), dis(v, t)) with its point (score) in the Cartesian plane. The first player in his/her turn chooses a vertical line and erases all the points on its left side. Second player in his/her turn chooses a horizontal line and erases all the point below it.
Each player tries to maximize his/her score.
Obviously, each time a player chooses a line on the right/upper side of his/her last choice. Imagine that there are A different x components x1 < x2 < … < xA and B different y components y1 < y2 < … < yB among all these lines. So, we can show each state before the game ends with a pair (a, b) (1 ≤ a ≤ A, 1 ≤ b ≤ B It means that in this state a point (X, Y) is not erased yet if and only if xa ≤ X and yb ≤ Y).

So, using dp, dp[a][b][i] (1 ≤ i ≤ 2) is the maximum score of i - th player in state (a, b) and it’s i - th player’s turn. So, consider s[a][b] is the sum of the scores of all valid points in state (a, b) and t[a][b] is the amount of them. So,
If i = 1 then, dp[a][b][i] = max(s[a][b] - dp[c][b][2]) (a ≤ c ≤ A, t[c][b] < t[a][b]).
Otherwise dp[a][b][i] = max(s[a][b] - dp[a][c][1]) (b ≤ c ≤ B, t[a][c] < t[a][b]).
So we need two backward fors for our dp and another for on i. So, now the only thing that matters is updating the dp. For this purpose, we need two more arrays QA and QB.
QA[b][1] = the minimum value of pairs (dp[j][b][2], t[j][b]) and QA[b][2] = minimum value of pairs (dp[j][b][2], t[j][b]) such that t[j][b] > QA[b][1].second in the states we’ve seen so far. Similarly, QB[a][1] = the minimum value of pairs (dp[a][j][1], t[a][j]) and QB[a][2] = minimum value of pairs (dp[a][j][1], t[a][j]) such that t[a][j] > QB[a][1].second in the states we’ve seen so far. Now updating dp is pretty easy :
dp[a][b][1] = s[a][b] - (t[a][b] ≤ QA[b][1].second?QA[b][2].first: QA[b][1].first).
dp[a][b][2] = s[a][b] - (t[a][b] ≤ QB[a][1].second?QB[a][2].first: QB[a][1].first).
And updating QA and QB is super easy.
Now, let f = dp[1][1][1] and S be the sum of scores of all points. So, the score of first player is f and the second one is S - f.
Time complexity: O(n2)
Let's call the answer for vertices v and u with edges e1, e2, ..., ek on the path, score of sequence w(e1), w(e2), ..., w(ek).
Use heavy-light decomposition. Decompose the edges into chains. So, for each Query, decompose the path into subchains. After solving the problem for them, combine them. Problem for subchains is :
We have an array a1, a2, …, an and q queries. Each query gives numbers x, y, l (1 ≤ x ≤ y ≤ n) and we should print the goodness of subarray ax, ax + 1, …, ay.

For this problem, we have too choices: 1.Solve offline with a normal segment tree. 2.Solve online using persistent segment tree. Now, I prefer to use the first approach. Sort the array to have a permutation of 1, 2, …, n: p1, p2, …, pn and ap1 ≥ ap2 ≥ … ≥ apn. Also sort the queries in the decreasing order of l. No for i - th query (in the sorted order) we have information: x, y, l, index.
Then, use two pointers. Keep a pointer = n and Initially we have a binary string b, of length n with all indices set to 0. Then in each query:
for i = 1 to q
while (pointer > 1 and l[i] >= a[pointer])
Set p[pointer]-th bit of b (from left) to 1
pointer = pointer - 1
answer to query number index[i] = T(bx…by)
Now, we should fins T(bx…Ty). For this purpose, we need a segment tree. In each node of the segment tree, we need to keep a package named node.
struct node{
int p, s, cnt, tot;
};
A package node is used for calculating T of a binary string c. p = the number of leading 1s, s = the number of trading 1s, cnt = the total number of 1s, tot = the T value of the binary string after deleting its leading and trading 1s.
Merging two nodes is really easy. Also after reversing c, we just need to swap p and s.
So, we can determine the node of this subarray in subchains.
After solving these offline for subchains it's time for combining.
Merge the node of subchains in the path from v to LCA(v, u) then merge the result with the reverse of the nodes of answers in the subchains in path from LCA(v, u) to u.
Time complexity: O((n + m)log2(n))
Code by PrinceOfPersia (This was one of the hardest codes I ever wrote in competitive programming :D)

If there's any suggestion or error, just let me know.
Hi.
Codeforces round #299 is gonna take place soon(exact time) and I'm the writer. I'm lucky to be the first Iranian author in Codeforces, in your and our new year (2015 and 1394).
Now, I wanna thank: myself(PrinceOfPersia) for writing the problems(:P), MikeMirzayanov for great Codeforces and Polygon platform, Zlobober and Damon and sobhan.miryoosefi for helping me prepare this round, Haghani and SoroushE for testing this round, Delinur for translating problem statements into Russian and big thanks to my great buddy, HosseinYousefi for problem legends and the pictures.
Also, I wanna thank MinakoKojima for teaching me how to use polygon and testlib and so much other things about it (about a year ago).
This is my first official contest(after all those contests in Gym :D). I hope you enjoy it.
The main character of all problems is Tavas, well-known by eating CoffeeMix without water! Trust me, when he does that it smells awful.

Also, you'll meet his friends.
I hope you enjoy the problems. I wish you all high ratings, many Accepted solutions and Successful hacking attempts. And Hacked instead of Failed System Test.
Scoring will be posted later.
GL & HF ;)
UPD: Scoring will be standard for both divisions (500-1000-1500-2000-2500).
UPD2: Contest is over. We're waiting for system testing. Editorial is published.
UPD3: System test is done. Congratulations to all winners.
Div.1 winners:
And Div.2 winners are:
Good job everyone, see you ;)
Welcome to the new episode of PrinceOfPersia presents: Fun with algorithms ;)
You can find all the definitions here in the book "Introduction to graph theory", Douglas.B West.
Are you in love with algorithms? If you are don't miss this round and be algorithm's valentine ;)

On the night before valentine's day (exact time), Valentine Algorithm cUp 2015 is going to take place.
There will be 6 problems and 3 hours to solve them. All of them are written by me(PrinceOfPersia).
This competition is like surprise languages but too different. 3 days before the contest, I will publish tutorial of 5 new algorithm languages(not programming languages) with their compiler codes. Each language is going to be really simple to learn and have at most 6 or 7 commands (they're not like programming languages).
Your program should print the code written in the language the problem says and checker will run it (pay attention that inputs are encoded, don't try to read form input, just print the code). Don't use unnecessary wjitespaces.
Each command of a language, will have a number, shown by w(x) called order. There will be a counter cnt = 0 (initially), every time your code calls this command, cnt increases by x. The order of your code equals the final value of cnt.
Each problem has a limit for your code's order.
If your code gets CE or OLE (order limited exceeded) or WA, you will receive Wrong answer.
Example :
Language (named EXM) : This language is built to process on an integer. There are two valid commands :
Your program returns the final value of that number.
Your task is given number n, the return value of your code must be number 2n + 1 .
Code in EXM:
M 2
I 1
C++ code (the code you will submit in submit page):
printf("M 2\nI 1\n");
Your code's order will be 2 + 1 = 3 .
UPD: You can download languages tutorial and their compilers here.
Attention: Compile the code for each language, in Windows : g++ -o lang lang.cpp -O2 -std=c++0x and in Mac and Linux g++ -o lang.out lang.cpp -O2 -std=c++0x.
Using in Windows:
For running your code that is saved in a file like x.txt, use exactly lang x.txt in cmd and if you want debug mode enabled, use lang x.txt -d (not lang -d x.txt).
Using in Mac OS X or Linux:
For running your code that is saved in a file like x.txt, use exactly ./lang.out x.txt in terminal and if you want debug mode enabled, use ./lang.out x.txt -d (not ./lang.out -d x.txt).
Sample problem:
Write a program in Prolan that given a string s containing only a and b deletes all bs and converts all as to d. Order shouldn't exceed 106 (1 ≤ |s| ≤ 100).
My code:
(b,)
(a,d)
If you have any question, feel free to ask.
UPD2: Scoring will be 500-1000-1500-2000-2500-3000.
By the way, the main characters of each problem is different from other problems. Actually, for each problem the main characters are an imaginary(or not!) couple :)
UPD3: IDXT's compiler had some bug, you can download the correct source here.
UPD4: For people who want to practice, the new archive(including languages tutorials and bugless compilers) can be found here.
In the last lecture of Algorithm Gym (Data Structures), I introduced you Segment trees.
In this lecture, I want to tell you more about its usages and we will solve some serious problems together.
Today I want to introduce you some very very useful data structures.
In this lecture, we are trying to improve your data structures skills, stay with us and click on read more.
You should make a sequence s1, s2, ..., sn such that si = a1 + a2 + ... + ai and use a binary search to find the first element that is greater than t % sn (or upper_bound function in C++ ).
Source code : Here
First of all, compute sequence f (0-based), then consider we have a sequence p (also 0-based) (partial sum), initially all members are 0.
For each query, if l < r, then do :
p[l] = (p[l] + f[0]) % mod;
p[l+1] = (p[l+1] + f[1]) % mod;
p[l+1] = (1LL * p[l+1] + mod - 1LL * ((1LL * b * f[0]) % mod)) % mod;
p[r + 1] = (1LL * p[r+1] + mod - f[r - l + 1]) % mod;
p[r + 2] = (1LL * p[r+2] + mod - 1LL * ((1LL * a * f[r-l]) % mod)) % mod;
otherwise, do this :
p[l] = (p[l] + f[0])%mod;
p[r+1] = (1LL * p[r+1] + mod - ((1LL * b * f[0])%mod))%mod;
p[r+2] = (1LL * p[r+2] + mod - 1LL * ((1LL * a * f[0])%mod))%mod;
An the just run this : for every i, staring from 0, pi + = a × pi - 2 + b × pi - 1 and ai + = pi .
Source code : Here
If we have an array x1, x2, ..., xm and for each i, 1 ≤ xi ≤ 60, the number of different element in the array y1, y2, ..., ym such that yj = lcm(x1, x2, ..., xj), is at most log(60!) .Because y1 ≤ y2 ≤ y3 ≤ ... ≤ ym and if yi < yi + 1, then yi ≤ 2 × yi + 1, and ym ≤ 60! .
Actually, it is even less, like 25.
So for each i, you can find all these members for array ai, ai + 1, ..., an using at most 25 binary searches and save them in an array.
And if x = p1b1 × ... × pkbk such that all pis are prime an k = the number of primes less than 60, then we assign sequence b to x. Using this, you can easily see that if x = p1b1 × ... × pkbk and y = p1c1 × ... × pkck, lcm(x, y) = p1max(b1, c1) × ... × pkmax(bk, ck). And for check if a number is less than another one using this sequence b, you can use log function and the fact that log(x) = log(p1b1) + ... + log(pkbk), so if log(x) < log(y) then, x < y, and this is how to calculate the minimum value.
By the way, you can calculate lcm(al, al + 1, ..., ar) in O(25) using Sparce Table.
Source code : Here
Consider, for each vertex v an each color c that there is at least one edge entering v with color c, we have the length of the shortest path from s to v such that it's last edge has color c (we call this dv, c). So, with this, you can make a graph with states (v, c) and run a Dijkstra on it and it's easy update.
But this will get TLE.
If you think about that, you don't need all states (v, c), among all these states, we just need the first two states with minimum value of d (for each vertex v).
Source code : Here
First of all, let's solve the 1-D version :
we have two sequences a1, a2, ..., an and b1, b2, ..., bn and for each i, we know that bi ≤ ai. Our goal is to calculate the number of pairs (l, r) in O(n) such that 1 ≤ l ≤ r ≤ n and max(al, al + 1, ..., ar) - min(bl, bl + 1, ..., br) ≤ k .
We use two double ended queues (deques) for this propose :
let mx, mn be two empty deques
l = 1
ans = 0
for r = 1 to n
while !mx.empty() and a[mx.back()] <= a[r]
mx.pop_back()
while !mn.empty() and b[mn.back()] >= b[r]
mn.pop_back()
mx.push_back(r)
mn.push_back(r)
while a[mx.front()] - b[mn.front()] > k
l ++
if mx.front() < l
mx.pop_front()
if mn.front() < l
mn.pop_front()
ans += r - l + 1
In this code, for each r we are finding the largest valid l, and by the way a[mx.front()] = max(al, al + 1, ..., ar) and b[mn.front()] = min(bl, bl + 1, ..., br) .
Now let's get back to the original problem.
For each pair (i, j) such that 1 ≤ i ≤ j ≤ m, build arrays a1, a2, ..., an and b1, b2, ..., bn such that ak = max(ak, i, ..., ak, j) and bk = min(ak, i, ..., ak, j) and then run the code above.
Except that C++ deque is too slow,so you should write one.
Source code : Here
For each row or column, it's not important how many times we run the operation on it, the only thing matters, is that it's odd or even.
So, assign a boolian to each row and each column, such that row number i's boolian is ri and column j's boolian is cj.
The other things are like 2-sat, except that the graph in this problem will be undirected.
For each query, if ax, y = bx, y so we know that  so add an edge between rx and cy and one between ¬rx and ¬cy.
so add an edge between rx and cy and one between ¬rx and ¬cy.
Otherwise, add an edge between ¬rx and cy and one between ¬cy and rx .
You can use a disjoint set with array or vector and in each step, check if a boolian like x and ¬x are in the same component, print "No" for the rest of the queries (Because when the answer to a query is No, the answer to the next queries will be also No).
Source code : Here
The other approach is to use binary search on the last step with answer "Yes" and check using a normal 2-sat (directed graph.)
Source code for this approach : Here
Use Robin-Carp. Let's consider that hi ≡ s1 × p0 + s2 × p1 + ... + si × pi - 1(mod m) .
For a query of type 2 or 3, just use a simple binary search.
For a modify query, if y = x - sp, you should add y × p0 to hp, y × p1 to hp + 1 and so on. You can do all these using a segment tree or fenwick (BIT).
Source code : Here
Use divide and conquer on the tree (centroid decomposition) and answer queries offline.
For conquer, imagine root is r. Run dfs on r and for each vertex, push it's distance to r in the vector e. Then sort e and for each vertex v in subtree of r and query o such that it's asking about v and number l, do this : ans[o] += the number of members of e like p such that p + d(r,v) <= l (using binary search).
But here, we counted some vertices for some queries more than once.
Then for each neighbor of r do this separately:
Run dfs on it's subtree and for each vertex, push it's distance to r in the vector z. Then sort z and for each vertex v in this subtree and query o such that it's asking about v and number l, do this : ans[o] -= the number of members of z like p such that p + d(r,v) <= l (using binary search).
Source code : Here
| Name |
|---|


