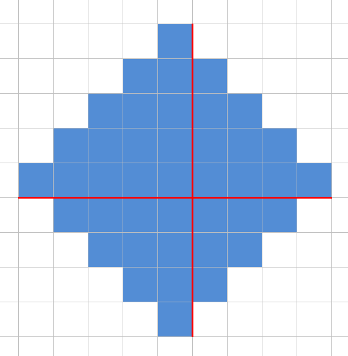
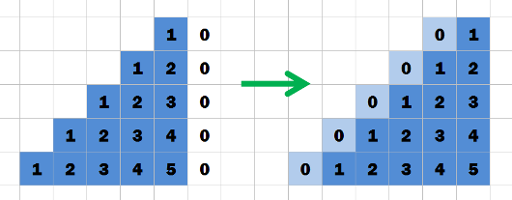
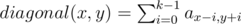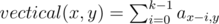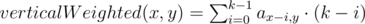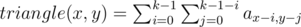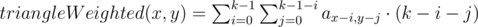The total number of different strings of 2 letters is 262 = 676, but the total length of the input strings is no more than 600. It means that the length of answer is no more than 2. So just check all the strings of length 1 and 2.
Build bipartite graph with n nodes for employees and m nodes for languages. If an employee initially knows a language, than there will be an edge between corresponding nodes. Now the problem is simple: add the minimal number of edges in such a way, that all the n employees will be in the same connected component. Obviously, this number equals to the number of initially connected components, containing at least one employee, minus one. But there is one exception (pretest #4): if initially everyone knows no languages, we'll have to add n edges, because we can't add the edges between employees (remember that the graph is bipartite).
For m = 3, n = 5 and m = 3, n = 6 there is no solution.
Let's learn how to construct the solution for n = 2m, where m ≥ 5 and is odd. Set up m points on a circle of sufficiently large radius. This will be the inner polygon. The outer polygon will be the inner polygon multiplied by 2. More precisely (1 ≤ i ≤ m):
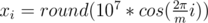
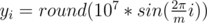
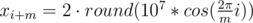
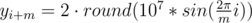
If m is even, construct the solution for m + 1 and then delete one point from each polygon. If n < 2m, delete 2m - n points from the inner polygon.
Unfortunately, this solution doesn't work for m = 4, n = 7 and m = 4, n = 8.
Another approach is to set up m points on a convex function (for example, y = x2 + 107), and set up the rest n - m points on a concave function (for example, y = - x2 - 107). Take a look at rng_58's solution — 3210150.
At first, notice that horizontal and vertical cuts are independent. Consider a single horizontal line. It contains m unit segments. And in any game state it's always possible to decrease the number of uncut units as the player wants. Imagine, that she starts growing a segment from a border, increasing it's length by 1 at a time. Each time the total uncut length decreases by either 0 or 1. In the end it obviously reaches 0.
The same holds for vertical lines as well. So if there are no initial cuts, the game is a nim with n - 1 piles of m stones and m - 1 piles of n stones. Could be solved with simple formula.
Initial k cuts should be just a technical difficulty. For any vertical/horizontal line, which contains at least one of the cuts, it's pile size should be decreased by the total length of all segments on this line.
How to make a first move in nim: let res is the result of state (grundy function), and ai is the size of the i-th pile. Then the result of the game without i-th pile is 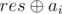 . We want to replace ai with some x, so that
. We want to replace ai with some x, so that 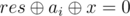 . Obviously, the only possible
. Obviously, the only possible 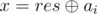 . The resulting solution: find a pile for which
. The resulting solution: find a pile for which 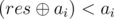 , and decrease it downto
, and decrease it downto 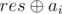 .
.
Suppose we have fixed set of inputs that we have to solve. Let's learn how to determine the optimal order. Obviously, Small inputs (and Large inputs with probFail = 0) won't fail in any case. It means that our penalty time is no less than submission time of last such ``safe'' inputs. So we will solve such inputs before all the others. Inputs with probFail = 1 are just a waste of time, we won't solve such inputs. Now we have only inputs with 0 < probFail < 1. Let i and j be two problems that we are going to solve consecutively at some moment. Let's check, if it is optimal to solve them in order i, j, or in reversed order. We can discard all the other inputs, because they don't affect on the relative order of these two.
(timeLargei + timeLargej)(1 - probFailj) + timeLargei(1 - probFaili)probFailj < (timeLargei + timeLargej)(1 - probFaili) + timeLargej(1 - probFailj)probFaili
- probFailj·timeLargej - timeLargei·probFailj·probFaili < - probFaili·timeLargei - timeLargej·probFaili·probFailj
timeLargei·probFaili(1 - probFailj) < timeLargej·probFailj(1 - probFaili)
timeLargei·probFaili / (1 - probFaili) < timeLargej·probFailj / (1 - probFailj)
Now we've got a comparator for sort, which will give us the optimal order. Note, that inputs with probFail = 0, 1 will be sorted by the comparator correctly as well, so it's not a corner case.
Let's return to the initial problem. First of all, sort problems with the optimal comparator (it's clear that any other order won't be optimal by time, and the score doesn't depend on the order). Calculate the DP: z[i][j] = pair of maximal expected total score and minimal expected penalty time with this score, if we've already decided what to do with the first i problems, and we've spent j real minutes from the contest's start. There are 3 options for the i-the problem:
skip: update z[i + 1][j] with the same expected values
solve the Small input: update z[i + 1][j + timeSmalli], the expected total score increases by scoreSmalli, and the expected penalty time increases by timeSmalli (we assume that this input is solved in the very beggining of the contest)
solve both inputs: update z[i + 1][j + timeSmalli + timeLargei], the expected total score increases by scoreSmalli + (1 - probFaili)scoreLargei, and the expected penalty time becomes timeSmalli + (1 - probFaili)(j + timeLargei) + probFaili·penaltyTime(z[i][j]), where penaltyTime(z[i][j]) is the expected penalty time from DP
The resulting answer is the best of z[n][i], (0 ≤ i ≤ t).
The expected total score could be a number around 1012 with 6 digits after decimal point. So it can't be precisely stored in double. And any (even small) error in calculating score may lead to completely wrong expected time (pretest #7). For example, you can multiply all the probabilities by 106 and store the expected score as integer number to avoid this error.
If there is no "binary" restriction, the solution is simple greedy. Each node of the tree (except the root) must have exactly 1 parent, and each node could be parent for any number of nodes.
Let's assign for each node i (except the root) such a node pi as a parent, so that ypi > yi and distance between i and pi is minimal possible. Renumerate all the nodes in order of non-increasing of y. Now it's clear that pi < i (2 ≤ i ≤ n). So we've just built a directed tree with all the arcs going downwards. And it has minimal possible length.
Let's recall the "binary" restriction. And realize that it doesn't really change anything: greedy transforms to min-cost-max-flow on the same distance matrix as edge's costs, but each node must have no more than 2 incoming flow units.