In this post I want to describe in short how to write a formulas on Codeforces. In fact it is short introduction to the markup language 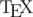 used on Codeforces.
used on Codeforces.
Three important rules.
Foremost rule: formula me place in dollars ($), as well as in parentheses.
Another important rule: if you want to apply some operation to some group of symbols it is necessary to form the block using the curly braces. For instance, 2^x+y = 2x + y, but 2^{x+y} = 2x + y.
Third rule — for perfectionists. For traffic economy Codeforces print simple formulas by usually text. Sometimes it is not very pretty: C_{x_i+y_i-2}^{x_i-1} = Cxi + yi - 2xi - 1. Is this case you can add command \relax at the beginning of the formula. Then the formula is guaranteed to be beautiful: \relax C_{x_i+y_i-2}^{x_i-1} = 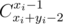 .
.
Arithmetic operations.
Addition and subtraction can be written ordinary symbols + and -. Multiplication is usually indicated by a null character (xy is the produst of numbers x and y) or by symbol  (
(\cdot). If it is necessary to multiply two complex expressions (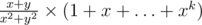 ), or are important both factors, not just the value of the product (in expressions of type field
), or are important both factors, not just the value of the product (in expressions of type field  ), use the symbol × , which may be obtained by the command
), use the symbol × , which may be obtained by the command \times.
The division is somewhat more complicated. Usually in mathematics division is not written in one line, but the desire is not to write the fraction of the blue, too, is understandable. In this case, you can always write a : or / (x:y, x/y).
If you want to write all the same fraction, it has two similar commands: \frac and\dfrac. After any of these commands have to write a block of the numerator and block of the denominator, for example:  (
(\frac{1}{4}). Using \frac small fractions are obtained, which is suitable mainly for the simple fractions. If you want to write a serious big fraction you'll need \dfrac: 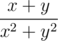 (
(\dfrac{x+y}{x^2+y^2}). If the numerator and denominator of a single-character, it can not be enclosed in brackets, for example: 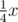 (
(\frac14x), but only if the numerator is not a letter.
The upper and lower indices.
If you want to write a lower index, you will help symbol _ and upper index (basically it is the exponent), the symbol^: (xi + yi)2 ((x_i + y_i) ^ 2). Same manner as with the fractions in the lower or upper index block can be placed, but if a single-character index, it can not do so.
Other useful tips and special characters
Text — text (---) — not in the formulas, and in the text. This dash, not hyphen (it is not works without surrounding text)
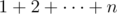 (
(\dots) — three dots symbol.
∞ (\infty) — infinity symbol.
 (
(\in) and  (
(\ni) — element of the set.
→ (\to) — arrow right, in expressions such as xn → 0.
Many well-known mathematical functions can be typed with the '\', then they will look like a formula, rather than simply as text (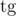 =
= \tg, 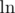 =
= \ln, 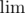 =
= \lim and so on)
If you want to index are top and bottom rather than the top-right and bottom-right, use the command \limits:
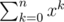 =
= \sum_{k = 0}^nx^k
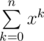 =
= \sum\limits_{k = 0}^nx^k.
If the brackets around a large expression small, you can make them suitable size, written before the left bracket command \left, and before right bracket command \right. For instance: 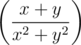 =
= \left( \dfrac{x+y}{x^2+y^2} \right).
Thank you for the attention!









 , where
, where 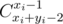 . We should subtract from that value all paths containing at least one of previous black cells. We should enumerate first black cell on the path. It could be one of previous cell that is not below or righter than
. We should subtract from that value all paths containing at least one of previous black cells. We should enumerate first black cell on the path. It could be one of previous cell that is not below or righter than 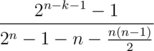 . Let use note that we can calculate only segments with
. Let use note that we can calculate only segments with 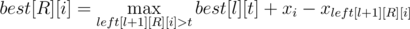 .
.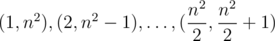 . We can to do it since
. We can to do it since  of these pairs.
of these pairs.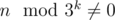 , and answer is
, and answer is 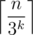 .
.
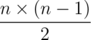 such pairs. Therefore we can make the array where we will mark pair who were meets. Lets iterate all pairs in any order until we meet repeated pair or pairs are ends. So we have solution of time
such pairs. Therefore we can make the array where we will mark pair who were meets. Lets iterate all pairs in any order until we meet repeated pair or pairs are ends. So we have solution of time 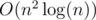 .
.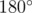 . Secondly, minimal angle is opposit to minimal side of triangle.
. Secondly, minimal angle is opposit to minimal side of triangle.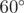 and this anlge is not least one. And side opposite to it is not least side. Therefore, if in
and this anlge is not least one. And side opposite to it is not least side. Therefore, if in 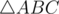
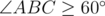 then
then 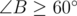 . For it lets sort all other points by the angle relative to
. For it lets sort all other points by the angle relative to 
