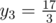This problem is hard because it might be impossible to consider a dynamic programming solution carefully and finally find the mystery.
Let dp[i][j]=(the minimum transformation price to the moment if y1... yi have been determined and yi = j).
It's easy to find that:
dp[1][p] = (p - x1)2
f[i][p] = min(dp[i - 1][q] | p - b ≤ q ≤ p - a)
dp[i][p] = (p - xi)2 + f[i][p]
Solutions using this idea straight can't pass because it needs very huge amount of memory and time(in fact it's infinite). So we should consider the problem more accurately.
Here comes the magic: let dp[i] be a function for p.
First of all, we'll use the monotonicity of its derivative dp[i]' and mathematical induction to prove that dp[i] is a strictly unimodal function. More strongly, we can prove dp[i]' is a strictly increasing function.
dp[1]'(p) = 2(p - x[1]). Obviously so it is.
If we have proved that dp[i]' is a strictly increasing function, and min dp[i] = dp[i](k). In addition, dp[i]'(k) = 0.
For f[i + 1] at this moment:
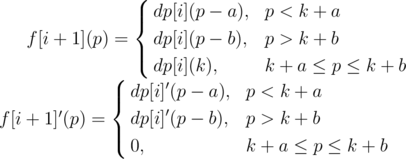
Notice that for the derivative, actually what we do is to cut dp[i]' at the place p = k, and then the left part (p ≤ k) moves to the right a units while the right part (p ≥ k) moves to the right b units. After this operation, the gap (k + a... k + b) is filled by 0 so that it's still a continuous function.
We can find f[i + 1]' is also a increasing function but not strictly. Then dp[i + 1]'(p) = 2(p - xi + 1) + f[i + 1]'(p), now it's absolutely a strictly increasing function.
Since we have proved any dp[i] is a strictly unimodal function, we can push xi one by one and calculate the function dp[i] immediately.
Let's focus on the operation to dp[i]':
Step 1. Determine k for dp[i]'(k) = 0.
Step 2. Cutting, translation, and filling 0.
Step 3. Add a linear function 2(p - xi).
Because of step 2, the derivative is in reality a piecewise function, and any part of this function is a linear function. Besides, there are at most O(n) parts.
Finally, We can use a simple array to hold all the endpoints. Since we should maintain at most O(n) endpoints for n times, the time complexity is O(n2).
Hint 1.
If you read the solution in earnest, you may have some questions.
Q: Why can't I use ternary search for every k?Or even binary search?
A: It's obviously right, but the time complexity is O(n2s) where s is times for the search. Either it will get TLE or the precision is not enough.
Just like this :) Questions are welcomed.
Hint 2.
Can we go beyond O(n2)?
Yes of course, by using some advanced data structures like a balanced tree with lazy tags. It's time for you to aftertaste and think more.
UPDATE
Figures from CMHJT for the input(not the sample input):
3 6 1 2
1 4 6
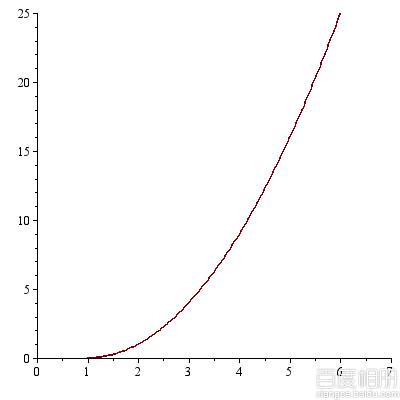
dp[1]:
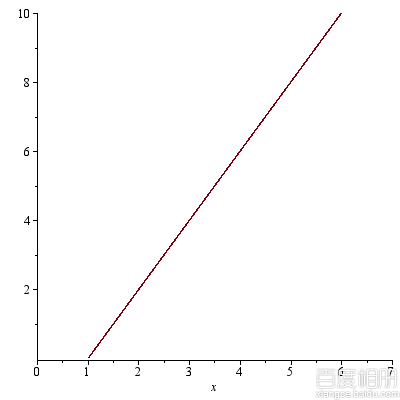
dp[1]':
dp[2]:

dp[2]':
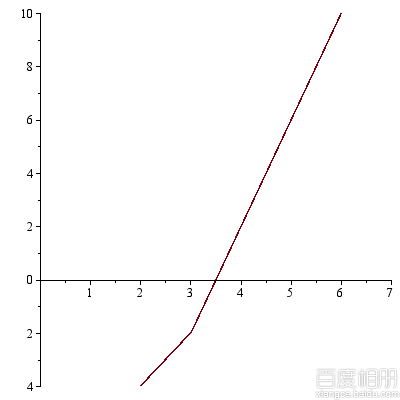
dp[3]:

dp[3]':

You can visually see that the minimum price is  when
when