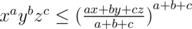Is anybody else also having the issue where they are unable to hide tags for unsolved problems? I uncheck the checkbox in the problemset tab but after some time has passed or after I have refreshed the page, the change is reverted and the tags are visible once again. This has been happening to me for more than a week now.
MikeMirzayanov, can you look into this?
Thanks!
UPD — The bug has not been fixed yet.
UPD 1-3-18 — The bug has not been fixed yet.
UPD 3-3-18 — The bug lives on.









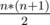
 .
.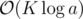
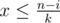 .
.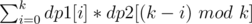
 from the answer for all such
from the answer for all such 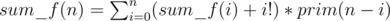
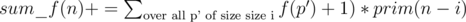
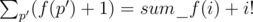
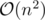 time.
time.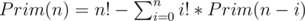
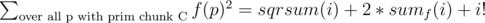
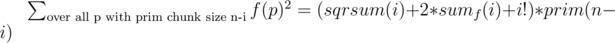
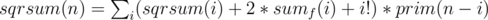
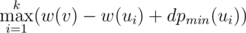 but in the sample solution
but in the sample solution 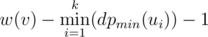 . How is that the same?
. How is that the same?