Two cases: t = 10 and t ≠ 10.
If t = 10 then there are two cases again :). If n = 1 then answer is - 1 (because there is not any digit divisible by t). If n > 1, then answer, for example, is '1111...110' (contains n - 1 ones).
If t < 10 then answer, for example, is 'tttttttt' (it, obviously, divisible by t).
The number of ways to choose ai (without any conditions) — 33n. Let A be the number of ways to choose ai with condition that in every triangle gnomes have 6 coins. Then answer is 33n - A.
Note that we can separate all gnomes on n independent triangles (i-th triangle contains of ai, ai + n, ai + 2n, i < n). So we can count answer for one triangle and then multiply the results. To count answer for one triangle, we can note that there are 7 ways to choose gnomes with 6 coins (all permutations 1, 2, 3 and 2, 2, 2).
So answer is — 33n - 7n. We count it in O(n).
Let's find a string that will be equal to s1 in k = n - t positions and equal to s2 in k = n - t positions. Let's denote q = quantity of i that s1i = s2i. If k ≤ q, then let's take k positions such that s1pos = s2pos and put in answer the same symbols. Then put in other n - k positions symbols, which are not equal to corresponding in s1 and s2 (we can do it, because we have 26 letters).
Now k > q. So, if there is an answer, where exists pos such that s1pos = s2pos, s1pos ≠ anspos, let's denote ansi = s1i, and then in any position such that s1i ≠ s2i = ansi and s1i = ansi (and in the same position in s2) we will choose ai, such that ai ≠ s1i and ai ≠ s2i (we can do it because k > q). So, for every position from q we can put symbols, equal to corresponding symbols in s1 and s2. Now we have strings s1, s2 of length n - q (such that s1i ≠ s2i for every i) and we should find string ans such that f(ans, s1) = f(ans, s2). We know that s1i ≠ s2i, so ansi may be equal to corresponding in s1 or to corresponding in s2 or not equal to s1i and to s2i. So, we need, at least, 2(k - q) symbols in answer to make f(s1, ans) = k - q and f(s2, ans) = k - q. Consequently, if n - q < 2(k - q), the answer is - 1, and else just put first k - q symbols in answer from s1, next k - q symbols from s2, and others won't be equal to corresponding in s1 and s2.
Solution works in O(n).
There is a fact that the distance between adjacent prime numbers isn't big. For n = 109 maximal distanse is 282. So let's find maximal prime p, such that p < n - 1 (we can just decrease n while it's not prime(we can check it in 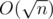 )). We know that n - p < 300. Now we have even (because n and p are odd) number n - p and we should divide it into a sum of two primes. As n - p < 300, we can just iterate over small primes P and check if P is prime and n - p - P is prime. You can check that there is a solution for all even numbers less than 300 by bruteforce.
)). We know that n - p < 300. Now we have even (because n and p are odd) number n - p and we should divide it into a sum of two primes. As n - p < 300, we can just iterate over small primes P and check if P is prime and n - p - P is prime. You can check that there is a solution for all even numbers less than 300 by bruteforce.
We can consider that we pay 2|i - j| coins for swap (we can divide answer in the end). Then we can consider that we pay |i - j| coins for moving pi and |i - j| for moving pj. So, if x was on position i and then came to position j, then we will pay at least |i - j| coins. Then the answer is at least 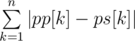 (pp — position k in permutation p, and ps — position k in permutation s). Let's prove that this is the answer by showing the algorithm of making swaps.
(pp — position k in permutation p, and ps — position k in permutation s). Let's prove that this is the answer by showing the algorithm of making swaps.
Let's consider that permutation s is sorted (our task is equal to it). Then we will put numbers from n to 1 on their positions.
How we can put n on its position? Denote ppos = n. Let's prove that there exists a position pos2 such that pos < pos2 and ppos2 ≤ pos(then we will swap ppos2 with n (and both numbers will move to their final positions and n will move to the right, so we can repeat this process until n returns to its position)). We can note that there are only n - pos positions that are bigger than pos. And how many numbers on these positions can be bigger than pos? We can say that answer is n - pos, but it's incorrect, because n is bigger than pos, but posn ≤ pos. Now we can use Pigeonhole principle and say that position x, such that x > pos and px ≤ pos exists.
But now our algorithm is O(n3). How we can put n in its position in O(n) operations? Let's move the pointer to the right while number is bigger than pos. Then swap n with found number. After we can move pointer from new n's position, so pointer always moves to the right and will not do more then n steps.










