978G-Petya's Exam
This is a greedy problem. First thing to notice is that exam which is occurring earlier compared to others should be prepared first, i.e. exam which is having less di should be prepared earlier(if value of s allows to do so).
Sort the exams in the increasing order of di. If we go through solution we can see that it gives optimum solution.
Let us take an exam from the sorted order = {si , di, ci}. Since we have sorted exams
 , 1 ≤ j ≤ n AND j ≠ i; either di ≤ dj or jth exam is completed(We are processing in increasing order of di). Now we have to prepare ci days for exam i in the interval si and di(and obviously we are forced to do so, so that's an optimal step). Now since all other exams(for which preparation is not done yet) are after ith exam, what is the best way to choose ci days in the interval [si, di] such that we leave better opportunities for the preparation of other exams?If we iterate from si to di and choose first ci days which are free for preparation. Hence our solution is optimal.
, 1 ≤ j ≤ n AND j ≠ i; either di ≤ dj or jth exam is completed(We are processing in increasing order of di). Now we have to prepare ci days for exam i in the interval si and di(and obviously we are forced to do so, so that's an optimal step). Now since all other exams(for which preparation is not done yet) are after ith exam, what is the best way to choose ci days in the interval [si, di] such that we leave better opportunities for the preparation of other exams?If we iterate from si to di and choose first ci days which are free for preparation. Hence our solution is optimal. Worst case time complexity is : O(m*n).









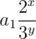 . Hence if
. Hence if 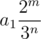
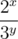 =
= 
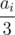 in sequence then
in sequence then 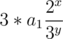 =
= 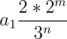 , this again is not possible by same argument as above, we just have to change the order of exponents.
, this again is not possible by same argument as above, we just have to change the order of exponents.

