Recently we were solving problems from past Indian ICPC regional . We weren't able to solve these 2 problems , and I couldn't find any editorial either . It would be really helpful if you guys can give me some hints to these problems.
Chemicals [Solved]
Description
There are N bottles each having a different chemical. For each chemical i, you have determined C[i], which means that mixing chemicals i and C[i] causes an explosion. You have K distinct boxes. In how many ways can you divide the N chemicals into those boxes such that no two chemicals in the same box can cause an explosion together?
Constraints
- T ≤ 50
- 2 ≤ N ≤ 100
- 2 ≤ K ≤ 1000
My Ideas
I thought of modelling the given dependencies as a graph and we are asked to find the number of ways to partition the graph into independent sets . But I realised that counting independent sets is intractable , so there must be a much more efficient or different way to solve this problem .
Solution
Thanks to ideas from fram and ABalobanov Since it's a functional graph we will have exactly one cycle per connected component . We need to color the graph using atmost K colors such that no 2 adjacent vertices have the same color . For any node which is not a cycle we have K - 1 options . For the nodes in a cycle we need to take care of them separately . We can construct a recurrence to find the number of ways to color a cycle in the following way.
Let DP[i] denote the number of ways to color a chain of length i such that it starts and ends with different colors.
DP[1] = 0, DP[2] = K * (K - 1)
DP[i] = (K - 2) * DP[i - 1] + (K - 1) * DP[i - 2]
This is basically saying that we have (K - 2) options for a chain starting and ending with different colors and (K - 1) options for a chain starting and ending with the same color. Another observation is that the number of chains of length i - 1 which starts and ends with same color is same as number of chains of length i - 2 which starts and ends with different colors.
My solution
Dividing Stones [Solved]
Description
There are N stones, which can be divided into some piles arbitrarily. Let the value of each division be equal to the product of the number of stones in all the piles modulo P. How many possible distinct values are possible for a given N and P?
Constraints
- T ≤ 20
- 2 ≤ N ≤ 70
- 2 ≤ P ≤ 109
Idea (thanks to ABalobanov)
We represent every partition as p1a1 * p2a2 * ... * pkak, where p1, p2, ..., pk are primes up to 70. We can achieve this value for a given n iff a1 * p1 + a2 * p2 + ... + ak * pk ≤ n . So the partition looks like p1 + p1...a1 times + ... + pk + pk...ak times , if the value is less than n we can add extra 1 .
My solution









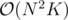 ) TLEs .
) TLEs .
