I found the following derivation using Lagrange multipliers for the solution of the Core Training problem in Code Jam this year. I liked this approach particularly because I don't get to use Lagrange multipliers very often in programming competitions.
Let 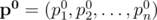 denote the initial vector of success probabilities that we are given, and let
denote the initial vector of success probabilities that we are given, and let 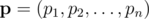 be an arbitrary vector of success probabilities. Let
be an arbitrary vector of success probabilities. Let  denote the probability of exactly i cores succeeding given the success probabilities in
denote the probability of exactly i cores succeeding given the success probabilities in 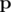 . Then we are trying to maximise
. Then we are trying to maximise

subject to
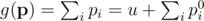
By using the Lagrangian method, we get that an optimal solution must satisfy
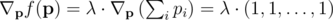
or it must be on the boundary (but we'll get to that later).
Lemma
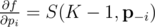
where 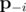 is the vector of probabilities with pi removed, i.e. (p1, p2, ..., pi - 1, pi + 1, ..., pn). That is, the partial derivative of f with respect to pi is the probability that exactly K - 1 of the cores succeed, not including core i itself.
is the vector of probabilities with pi removed, i.e. (p1, p2, ..., pi - 1, pi + 1, ..., pn). That is, the partial derivative of f with respect to pi is the probability that exactly K - 1 of the cores succeed, not including core i itself.
Proof of Lemma
This is a somewhat well-known derivation, but I have included it for completeness. By expanding the terms,
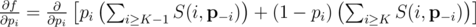
which simplifies to

(End proof.)
In order to have 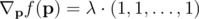 , then the most obvious thing to do is to set all the pi equal to each other. However this is not possible, since we cannot reduce pi below p0i. By taking into account boundary conditions, this then gives us three choices for each core i:
, then the most obvious thing to do is to set all the pi equal to each other. However this is not possible, since we cannot reduce pi below p0i. By taking into account boundary conditions, this then gives us three choices for each core i:
- We leave pi at its initial value p0i.
- We increase pi to 1.
- We try to equalise pi with the some other {pj} that are not on the boundary.
This observation is sufficient to restrict the solution space to the point where we can search over it. (Well, we still need to make some efficiency arguments, like "only increase pi up to 1 if it is already big", and "only try to equalize pi's that are close to each other", etc..., but you get the idea.)