540A - Combination Lock

For every symbol we should determine how to rotate the disk. This can be done either by formula: min(abs(a[i] - b[i]), 10 - abs(a[i] - b[i])) or even by the two for cycles: in both directions.

540B - School Marks

First count the number of marks that are less than y. If there are more than 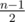such marks, we can't satisfy the second condition (about the median), and the answer is -1. Otherwise we can get exactly such number of y marks so that the total number of marks greater than or equal to y is at least 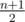(maybe it's already satisfied). This is the required action for satisfying the second condition.

Now, in order not to break the first condition, get the remaining marks as lower as possible — all ones — and check the sum of the marks. If it is greater than x, the answer is -1, otherwise the correct answer is found.

540C - Ice Cave

There are three cases here, though some of them can be merged.

1. If the start and finish cells are equal, let's count the intact neighbours of this cell. If there is one, move there and instantly move back — the answer is YES. Otherwise it's NO.
2. If the start and finish cells are neighbours, the solution depends on the type of the destination cell. If it's cracked, the answer is YES — we can just move there and fall down. Otherwise it must have at least one intact neighbour to get the positive answer — we can move to the finish cell, then to this intact neighbour, and then return to the finish cell.
3. In the general case, check if the path from the start cell to the finish cell exists. If it doesn't, the answer is NO. Otherwise check the type of the destination cell. If it's cracked, it must have at least one intact neighbour, and if it's intact, it must have two intact neighbours.

540D - Bad Luck Island (my code: http://pastebin.com/3s6dRK3A)

Let's count the values dp[r][s][p] — the probability of the situation when r rocks, s scissors and p papers are alive. The initial probability is 1, and in order to calculate the others we should perform the transitions.

Imagine we have r rocks, s scissors and p papers. Let's find the probability of the rock killing scissors (the other probabilities are calculated in the same way). The total number of the possible pairs where one species kills the other one is rs + rp + sp, and the number of possible pairs (rock, scissors) is rs. As all meetings are equiprobable, the probability we want to find is 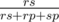. This is the probability with which we go the the state dp[r][s — 1][p], with the number of scissors less by one.

In the end, for example, to get the probability of the event that the rocks are alive, we should sum all values dp[i][0][0] for i from 1 to r (the same goes to the other species).

540E - Infinite Inversions (my code: http://pastebin.com/QFEMRbNP)

At first find the position of each element which is used in swap (using map). Now let's find the answer. It consists of the two parts. First part is the number of inversions formed by only whose elements which took part in the swaps. They can be counted by one of the standard ways: mergesort or Fenwick tree. The second part is the number of inversions formed by pairs of elements where one element has been swapped even once, and the other element stayed at his position. Let's consider the following test:

2
2 6
4 8

The global sequence will look as follows: [1 6 3 8 5 2 7 4 9 ...], and here is the array of swapped elements: [6 8 2 4].

Let's understand with which numbers the number 8 forms the inversions. The only elements that could do that are the elements between the initial position of the number 8 (where the number 4 is now) and its current position: [5 2 7]. There are two numbers on this segment which didn't take part in swaps: 5 and 7. The number 2 should not be counted as it took part in the swaps and we have already counted it in the first part of the solution.

So we should take the count of numbers between 8's indices in the global sequence (8 - 4 - 1 = 3) and subtract the count of numbers between its indices in the swaps array (4 - 2 - 1 = 1). We'll get the number of inversions formed by the element 8 and the elements which haven't moved at all, it's 2. Counting this value for all elements which have been swapped at least once, we get the second part of the answer. All operations in the second part of the solution can be performed using sorts and binary searches.

Hi all,

I was honored to open the fourth hundred of Codeforces Rounds. Unfornunately, neither I nor my friends couldn't invent any hard problems, so it's only a Div. 2 Round. But we'll definitely prepare a full round in the future! As always, I thank Zlobober for his help in preparing the problems, Delinur for English translations and MikeMirzayanov for the Codeforces itself.

The problems must be pretty easy for Div. 1 guys, so let's start a challenge: reds should solve everything in 30 minutes, yellows — in 1 hour, and violets — in 1 hour and a half. How many people will be able to make a success?

The score distribution will be standard. Wish you accepted solutions and successful hacks!

UPD 1. Congratulations to the winners in Div. 2:

1. PauGra
2. cuvwqe496
3. tgehr

and in Div. 1:

1. niyaznigmatul
2. I_love_Tanya_Romanova
3. dreamoon_love_AA

UPD 2. This is the editorial: /blog/entry/17643.

Hello guys,

I'm going to tell you about one of the negative aspects of Java on programming contests (actually, not only on contests), or, more precisely, how I have tried to resolve it. As you may know, Java has the disadvantage related to its collections library: the constraints of this language make you use object types even when using primitive types should be enough. Compare ArrayList<Integer> and vector<int>: Java list stores objects of type Integer, which are created every time when you add an element into the list (it's called boxing / unboxing), whereas C++ vector just stores ints. This behaviour slows down Java programs, and many people don't like it.

All this shit comes from the language design: you can't simply write a primitive type inside the angular brackets in Java. Some months ago I was thinking about this problem and came to the solution: why not just write my own collections library, with primitive types? Moreover, I haven't found any library with really all collections in the Internet.

That's how my small project EZ Collections (Github repository) was born. Of course, I haven't written all possible collections for all possible datatypes. Instead of that I have written each collection only once, leaving some hints for Maven plugin to generate everything as needed.

I have to say that this library is designed to use on programming contests or private purposes. It's thread-unsafe, it has some missing validations, it's prohibited to modify the collection during the iteration, it doesn't support serialization and maybe something else. But the problems on the contests can be solved without any troubles.

To use this library, you need:

1. Install Git and download the repository using git clone command (the URL is specified on the main page of the project). Or you can just download it using Download ZIP button.

2. Download Maven (link to the download page), install and configure it (if you don't know anything about it — use Google, but, as far as I remember, it's enough just to set the path to Maven in the system variables).

3. Enter the root directory of the library and execute command mvn clean install. After that two jar files will appear in your local Maven repository, and also in the target folder. One of these jars contains class files, and the other one — source files. Now you can use them in your Java project.

But it's still unclear how to use it on contests. You need Egor's plugin CHelper for IntelliJ IDEA. After it had moved to Github, it became possible to merge the pull request that fixes some problems. The last pre-built version (commit 29dc20b), which includes my pull request, can be downloaded from here and installed in IDEA on your own.

After plugin update you can include the library into your contest project, specifying the path to the jar file with sources. That's all!

This is the example: let's solve the problem 118E - Bertown roads

• use List<Integer>[] for storing the graph: 8293080 — 1060 ms, 39100 KB
• use EzIntList[] for storing the graph: 8293086 — 654 ms, 12148 KB

(this problem has quite large input, the larger it is, the more performance you gain)

One more example: solve the problem Timus 1521

With the TreeList's help the solution takes only a few lines:

int n = in.readInt();
int k = in.readInt();
EzIntList a = new EzIntTreeList(n);
for (int i = 0; i < n; i++) {
    a.add(i);
}
int idx = 0;
for (int i = 0; i < n; i++) {
    idx = (idx + k - 1) % a.size();
    out.print(a.removeAt(idx) + 1);
    out.print(' ');
}

What do we get using EZ Collections? For now, the following data structures are implemented:

• ArrayList
• ArrayDeque (with the possibility to get the element by its index)
• Heap
• Sort (guaranteed NlogN implementation)
• HashSet
• HashMap (I've used open addressing approach. I'm quite sure that it's not hackable)
• TreeSet
• TreeMap
• TreeList (the array that can perform add, set, insert and removeAt operations in logN time)
• Pair classes

Also I have to mention that there is famous Trove library (its repository can be found here) which has the similar idea, maybe some of you use it at work, but the problem is that only ArrayList, HashSet and HashMap are implemented in Trove. It's not enough for programming contests.

Some notes and plans:

• NaN, POSITIVE_INFINITY and other similar stuff is not supported. You know who you are, if you use such things.

• As it's impossible to return null (because EZ Collections store primitive types), method returnedNull() is added in every class where it's necessary. You must call it to perform null-check immediately after calling the method which could have returned null in usual Java Collections. For instance, these code fragments are identical:

    TreeSet<Integer> set = new TreeSet<Integer>();
    Integer lower = set.lower(42);
    if (lower == null) {
        ...
    }

    EzIntTreeSet set = new EzIntTreeSet();
    int lower = set.lower(42);
    if (set.returnedNull()) {
        // don't use the lower variable, it's not guaranteed that it has some certain value
    }

• The current source generation mechanism is ugly and doesn't support some cases that I want to support, so I'm planning to rewrite it. But all collections I wanted to implement in the first version already work.

• boolean is considered to be uncomparable type, so Pairs with booleans don't implement Comparable. It will be fixed after rewriting the source generation.

• Next collections I want to implement are LinkedList (on arrays). But it's only when I rewrite the source generation.

• The next planned thing is to implement maps which have primitive key and object value types, or vice versa. It also should speedup programs a bit.

Please write any suggestions and feedbacks using the private messages on Codeforces.

Version history:

• Feb 21, 2015 — version 0.1.0 is released. It contains the identical content comparing to standard Java collections library.
• Mar 15, 2015 — version 0.1.1 is released. TreeList was added. Also the possibility to specify custom hash functions for HashSet/HashMap was added.

Recently we ran another ACM ICPC quarterfinal qualification contest, whose results influenced the list of teams that will go to Saratov this autumn. The corresponding gym contest on Codeforces will be held on Sunday, Sep 21, 2014, at 11:00 AM.

Link to the contest: 2014, Samara SAU ACM ICPC Quarterfinal Qualification Contest

The list of our previous contests:

• 2012, V Samara Regional Intercollegiate Programming Contest
• 2012, Samara SAU ACM ICPC Quarterfinal Qualification Contest
• 2013, VI Samara Regional Intercollegiate Programming Contest
• 2013, Samara SAU ACM ICPC Quarterfinal Qualification Contest
• 2014, VII Samara Regional Intercollegiate Programming Contest

Link to announcement and discussion.

And here is the problem analysis.

A div 2: 378A - Playing with Dice

Make three counters: for wins of both players and for a draw. Iterate over all six ways how they can throw a dice. For each way determine who wins or there is a draw and increment the corresponding counter.

B div 2: 378B - Semifinals

You can think a bit and understand that you should consider only corner cases: k = 0 and . All other cases will be something between them.

If k = 0, we should choose n biggest elements from two sorted lists, one of the ways is to use two pointers method. And if , we just mark first people in each list.

A div 1 / C div 2: 377A - Maze

Start BFS or DFS from any free cell. As the maze is connected, this search will visit all s free cells. But we can stop the search when it visits s - k free cells. It's obvious that these s - k cells are connected to each other. Remaining k cells can be transformed into the walls.

Solutions which every move transform the cell which has the minimal number of neighbours passed pretests. However, it's wrong. Here is the counter-test:

....
.#..
..##
..##

Top-left cell has no more neighbours than any other cell but we cannot transform it into the wall.

B div 1 / D div 2: 377B - Preparing for the Contest

It's obvious that the time needed to fix all bugs is the monotonic function: if we can do it for some time, we can do it for greater time. So we can use binary search in these problem. We should learn how to check if some time t is enough.

At first sort all bugs by their complexity and all students by their skills. Let's consider the hardest bug. Who can fix it? It can be fixed by student whose skills is not less that this bug's complexity. Push all such students into the priority queue (sorted by students' price) and pop the cheapest student. As we check time t, this student must fix t hardest bugs (he definitely can do it). Save that information and go to the next bug which has not been fixed yet. Again push all students which can fix it to the priority queue and pop the cheapest one. And so on. If at some moment priority queue is empty, time t is not enough. If we spent too much 'money' — it's not enough as well. Otherwise we get the correct schedule.

C div 1 / E div 2: 377C - Captains Mode

There are some observations that do the problem very simple. The first one is that we always should pick the strongest hero. But we cannot say something similar about the bans — in different situations different bans are the best. But the most important observation is that we should consider only m strongest heroes. Indeed, in every game where only strongest heroes are picked, no hero except m strongest can be picked. That's why we don't need to ban them and therefore we don't need to consider them.

So now we have only 20 heroes. It means we can solve the problem using the dynamic programming with bitmasks: dp_mask will be the difference between the teams' strengths when only those heroes are picked or banned whose bits are set to 1 in the mask. At every state we try to pick or ban every available hero and go to the other state. The simpliest way to implement it is the recursion with memoization. The answer will be stored in dp_2^m - 1.

Unfortunately, we couldn't estimate the real complexity of this problem (despite it has the simple solution, this solution is not so easy to think of — standard 1500 points for problem C would be better) and set too big TL (many solutions written in C++ whose complexity is m²·2^m passed — we should have been set TL to 1 second or even to 0.75 seconds). So if you solved it in m²·2^m, you may assume that you're just lucky and your correct verdict is Time Limit Exceeded.

Why it can be solved in m·2^m? There is no point of missing a ban — if we ban the weakest hero, nothing will change since the weakest hero won't be picked.

Also this problem has weak pretests so you could hack solutions without bitmasks with almost any big random test.

D div 1: 377D - Developing Game

Let's note that every answer is characterized with two numbers L and R so that max{l_i} ≤ L, R ≤ min{r_i}, and L ≤ v_i ≤ R. If we know L and R, we can check every person and choose those who satisfies the conditions above.

Let's imagine a plane with the coordinate axes: one of the axes will be L, and the other will be R. If the point (L, R) on this plane is the optimal answer, people included in this answer for sure satisfy the conditions l_i ≤ L ≤ v_i and v_i ≤ R ≤ r_i. These conditions specify the rectangle on the plane. Since we should find the maximum number of people, we should find such point (L, R) that it is inside the maximum number of the specified rectangles.

Now it's the standard problem that can be solved using the scanline through one axis and the segment tree built on the other axis. The hardest part is to reduce the original problem to it.

E div 1: 377E - Cookie Clicker

First of all, throw away the buildings which cannot be used in any optimal answer: for each v_i remain only one building that has speed equal to v_i and minimal c_i. Also throw away all buildings whose speed is less than the speed of the fastest building which has c_i = 0.

It's fairly obvious that at any time we should use the fastest building. And if some building is used in the optimal answer, it should be bought and used immediately when we have enough money (I will use the word 'money' instead of 'cookies').

Let's imagine the plane (x, y) where x axis stands for the time and y axis stands for the money. We will maintain the graph of the function y = f(x) — 'maximal number of money that can be obtained at the time x' and process the buildings one by one, changing the graph. This function is the union of the line segments with the slopes equal to v_i, and each of these line segments is active on a certain segment [x_li, x_ri] of the axis x.

For example, at the beginning the graph is just the line y = v₁x, where v₁ is the speed of building that can be bought for 0 units of money. Let the next building's price is c₂. Find the minimal point x₀₂ where value of our function is greater or equal to y = f(x₀₂) ≥ c₂ and buy this building at the moment x₀₂. Then we should make the line y = y₀₂ + v₂x where y₀₂ = f(x₀₂) - c₂ is the amount of money remaining after the purchase. Now we have two lines. Till some moment the first line is better (not till x₀₂, maybe later), but as v₂ > v₁ there exists a moment of time (it's ceil(x₁₂) where x₁₂ is the x-coordinate of the lines' intersection) when the second line becomes better. Now we know the segments where a particular line is better than the others.

Continue add all buildings to the graph this way. Line segments should be stored in stack, as in all problems with convex hull, and every step remove unnecessary line segments from the stack (these are the lines those position in the stack is after the line which has an intersection with the currently added line). After we process all buildings, we use our graph to find the minimal time when we have S untis of money.

If we also should say which building we must use, we can store for any line segment its 'parent' — the line segment which was active when the current one was bought. With such parent array it's not hard to restore the sequence of buildings in the answer. We removed this part from the problem to make it a bit easier.

Hi all!

Authors of today's round are craus and dalex. We just couldn't miss the round with such a beautiful number, so at 19.30 MSK you will solve problems which were invented by Pavel and prepared by me.

We thank Gerald and Delinur for their help in contest preparation and MikeMirzayanov for creating Codeforces.

Scoring system and score distribution will be published when the round starts. Anyway this information makes no sense unless the round begins.

We wish you accepted solutions and successful hacks!

UPD. Contest is over, congratulations to the winners!

Div. 1:
1. Petr
2. tourist
3. Egor

Div. 2:
1. k3e18
2. tongcx1988
3. LeMieux

UPD. 2 Problem analysis is published.

As the admins don't want to fix the bug with two different Codeforces sites (1 2), I ask you to paste relative links.

It can be done this way:

• /profile/tourist

• /blog/entry/1

• /contest/1/problem/A

If you click on such link, you won't be logged out. Thanks.

On Satudray, Oct 12, at 12:00 PM another 5-hour contest in Codeforces Gym will be held. It's the second time we prepare qualification contest for Samara SAU teams to determine who deserves to participate in Southern Subregional Contest in Saratov (the previous such contest can be found here).

Maybe you know that team Teddy Bears is no longer able to take part in ACM ICPC. It resulted in renaming and renumbering the teams in the university. You have an unique opportunity to defeat new first team of Samara SAU and show them at what place they can finish in Subregional Contest. Don't miss this chance!

Contest is over. Now you can just solve the problems or take part in the virtual contest.

Many thanks to Xellos who made a tutorial.

I just leave the test generator here: [Codeforces] [Ideone] [Pastebin]

UPD. The similar blog entry about Java 6: http://codeforces.com/blog/entry/2296 (it's only in Russian, but you can look over source code)

UPD 2. The link was updated. Generator's speed was increased a bit. However, it seems that something works wrong and for some array sizes it generates easy-to-sort array. Always check if sort really works slow.

UPD 3. Links were updated again. It works almost just as planned now. There is still one issue that I don't know how to fix, but in general it works and can be used.

Hi all!

Today, June 12, when Russia celebrates Day of itself, Euro 2012 second round starts and I_love_natalia has a birthday, we present you Codeforces Round #124.

Contest was prepared by team Samara SAU Teddy Bears (craus, dalex, Hohol) and I_love_natalia. Also thanks to Alex_KPR and Codeforces team (Gerald, Delinur, MikeMirzayanov). We think that contest is very easy, and your task will be prove of refute this assertion :)

Scoring system is dynamic (Learn more about dynamic problem scoring).
Authors think that problems are sorted by difficulty in non-descending order.

Accepted solutions and successful hacks to you!

UPD. Contest is over, congratulations to the winners!

Div-1 (full results):

1. tourist — the only one who solved all problems!
   
2. RAVEman
   
3. aropan
   

Div-2 (full results):

1. bmerry
   
2. littlefriend
   
3. gstsclq
   

UPD 2. Tutorial is available.

One minute remaining! Don't forget to participate! :)

http://code.google.com/codejam/

UPD: Results: http://code.google.com/codejam/contest/1645485/scoreboard?c=1645485#

First 1000 contestants pass to the next round.

Hello.

I and I_love_natalia just discovered a strange problem which came to me when I generated antiquicksort-test. I even got an unsuccessfull hack on today's round because of it. It was surprising to me that my victim's program had worked so fast on the antiquicksort test. But at the end of the contest I changed the size of array in the generator from 100000 to 99987, and the hack became successful!

I don't know why it happens. This is the test case:

1. Run test generator from http://pastebin.com/99RwHR6w in Codeforces Custom Test interface.

2. Server will output you something like Sorting ended in 1953ms

3. Add two empty lines to the end of the code and run it again.

4. Result is: Sorting ended in 0ms.

You can add and delete spaces and empty lines from random places of the code and the results will be different: array can be sorted in zero time or in about 2 seconds.

I uploaded a video with this issue, you can download and watch it: link (be careful, being unzipped, it is about 600 MB)

So what is it? A bug of Java virtual machine? Or Codeforces server tries to protect contestants from antiquicksort?

UPDATE: As it turned out, some Codeforces servers have Java 7. Java 7 has other implementation of sort, so that's why some runs on antiquicksort tests are fast. It is not good because I submit my solution under Java 6 but it can run under Java 7 instead. Please note it till admins fix that issue.