381A - Sereja and Dima
Simply do the process described in the statment.
381B - Sereja and Stairs
Calculate the amount of each number. For all the different numbers — maximum possible times of use isn't more than 2 times. For the maximum is is only — 1.
380A - Sereja and Prefixes
Generate the first number 100000. Will in turn handle the requests, if the request gets to the point of adding one number, just print it. Otherwise see what element will meet our and just print it from precalculated array.
380B - Sereja and Tree
Lets generate a tree as described in the statment. For each request to add items we just add a segment for a certain level. At the request of the number of items we just go through all the lower levels, considering the leftmost and the rightmost vertex in the subtree. To each level will take all intervals that it owns and for each check — whether it intersects with the interval that we have generated in the current stage. If so, simply add items to the set. The complexity of solving O(n·m).
380C - Sereja and Brackets
We will support the segments tree. At each vertex will be stored:
av — the maximum length of the bracket subsequence
bv — how many there it open brackets that sequence doesn't contain
cv — how many there it closed brackets that sequence doesn't contain
If we want to combine two vertices with parameters (a1, b1, c1) and (a2, b2, c2), we can use the following rules:
t = min(b1, c2)
a = a1 + a2 + t
b = b1 + b2 - t
c = c1 + c2 - t
380D - Sereja and Cinema
In order that no one would be upset, every person except first should sitdown near someone else. Now when any human comes we know that for one side of him there will not be any people. Will use it. We will support the interval exactly occupied seats. If the first person is not known, it is possible that we have 2 such intervals. Now only remains to consider carefully all the cases that could be, because at each iteration we know exactly how many people will sit on some certain place.
380E - Sereja and Dividing
Note that at any particular segment we are interested not more than 60 numbers. The greatest number enters with a coefficient of 1/2, the following — 1 /4, 1 /8, and so on. Thus to solve the problem we need to know for each number: how many segments to include it as a maximum , as a second maximum , a third , and so on until the 60th .
What to know such information is sufficient to find 60 numbers large jobs left and right. This can be done carefully written the set or dsu.
Now, with this information we can calculate by countind number of segments which contain our element. It is not difficult to do, knowing the positions of elements , large then current . Let the position of elements on the left: p1> p2> ... > Ps1. And positions right: q1 < q2 < ... < qs2. So we should add value 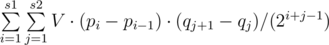 .
.
All details can be viewed in any accepted solution.











Thanks Sereja
What a speedy tutorial!
I wonder how fast are you!
This is so obviously Google Translated. Look at the first sentence of div1 A: "100000 numbers" is translated as "number 100000". Nobody who knows English at least a little bit would reverse the order of words like that.
Needless to say, I really don't understand the solutions from it. At least I know a bit of Russian :D
Yap, it's kinnda hard to understand in this Google-Translated form. Could anybody care to take their time and rephrase the explanation a little since I had troubles solving the problem? (380A — Sereja and Prefixes). Thanks !
Here's the solution I came up with afterwards. (I think it's the same as the one described in the editorial)
First, calculate the first 105 numbers. This suffices because we know all the l's are within the range of 1 to 105, so all numbers created by the second type operation can be found in the first 105. Additionally, save the index of each of the type 1 operations. (save the position of each number)
Then, given the queries from q1 to
Unable to parse markup [type=CF_TEX]
, we can check two things: 1) If qi is in the set of indexes covered by type one operations, we are done. This is because we can just use a binary search to find the correct answer. 2) If qi is not, we can find which type 2 'range' qi is in. We can find the k such thatUnable to parse markup [type=CF_TEX]
for some x. Then, we can simply takeUnable to parse markup [type=CF_TEX]
, and this basically proves thatUnable to parse markup [type=CF_TEX]
, whereUnable to parse markup [type=CF_TEX]
is in the first 105 integers. (and so we can just look it up from the original calculations).sorry if the explanation isn't very good, I may revise it later.
EDIT: added latex (it says revision 8 because my internet was slow and I clicked it multiple times)
EDIT 2(9): The ranges you can calculate at the beginning, just make a matrix
Unable to parse markup [type=CF_TEX]
and a number calledUnable to parse markup [type=CF_TEX]
. When you scan in each line, you letUnable to parse markup [type=CF_TEX]
. Then, if it is type 1, you add one toUnable to parse markup [type=CF_TEX]
, and if it is type 2, you addUnable to parse markup [type=CF_TEX]
toUnable to parse markup [type=CF_TEX]
.thanks for the explenation, i think it is very clear.
thanks a lot, I couldn't wrap my head around why the limit is 10**5 for storing sequence
Find out the maximum value of L .. All the array indices queried will depend on either provided value when type 1 is used as a input or on staring 1st L values when Type 2 is used .... Use a array to store 1st L values ... and Map can be used to store value larger than L when type 1 is given... Answer the query using this array or map used
:o Really weird that I missed that particular solution to C, I like such tricks with segment trees. But fortunately I came up with another solution. Let's calculate two arrays sum_pref_all, sum_pref_end. In order to calculate first, change ( to 1 and ) to -1 and calculate prefixes' sums. In order to calculate second change ( to 0 and ) to 1 and calculate prefixes' sums. Answer is 2 * (sum_pref_end[r] — sum_pref_end[l — 1] — sum_pref_all[l — 1] + c) where c is equal to min(sum_pref_all[l — 1], sum_pref_all[l], ..., sum_pref_all[r]. First part sum_pref_end[r] — sum_pref_end[l — 1] is a number of all ')' in this subword and sum_pref_all[l — 1] — c is a number of ')' which can't find their corresponding '('. In order to retrieve c of course build a segment tree.
UPD: I have updated this post, since I messed up sum_pref_all and sum_pref_end in few places.
I also have a very different solution for problem C (Div1). First I used a stack in order to match each closing paranthesis to the closest unmatched open paranthesis before it (if any). In the optimal answer for any query, a closing paranthesis is either matched with that open paranthesis or with none (I did not really prove it, but it seems reasonable). Then the problem becomes: for a given query [L,R] count how many intervals [x,y] are contained within [L,R] (where x is the position of an open paranthesis and y is the position of its matching closing paranthesis, if any). In order to solve this problem easily I sorted the queries by their left endpoint and handled them in this order. I also maintained a segment tree with the right endpoints of the intervals [x,y] such that x>=L (where L is the left endpoint of the current query). Answering a query then consists of simply computing a prefix sum for the interval [1,R] (i.e. how many right endpoints of intervals [x,y] with x>=L are located before or at the position R). Note that since we sorted the queries, when advancing from one query [L1,R1] to the next one [L2,R2], we remove from the segment tree the right endpoints of intervals [x,y] with L1<=x<L2 (if any). Then, a prefix sum is actually the same as the sum over the interval [L,R] (because there will be no more right endpoints in the segment tree located before L). A binary indexed tree can also be used instead of a segment tree.
In fact, I tried very similar approach during the contest but couldn't debug it within time :(. My approach is as follows:
Let the input string be the variable str[]. For each opening bracket ('(') find the corresponding matching closing bracket (')') and store the index in an array (say store[]). This can be done using stack as mugurelionut mentioned. Now, sort the queries (L,R) using the L value.
Now consider a Binary Indexed Tree, which is initialized as follows: the value of tree[store[i]] is 1, if str[i] is '(' and it has a matching closing bracket (ie., store[i] is valid) else it is 0. Now, for each query the required answer is the 2*(prefix-sum[R] — prefix-sum[L-1]) which can be calculated easily using BIT. The catch is when moving from one query to another (note they are sorted) , say [L1, R1] to [L2, R2] where L1 <= L2, you update the value of tree[store[L1]] = 0, tree[store[L1+1]] = 0 ... tree[store[L2-1]] = 0 (update only when the store[] values are valid for the given index).
This is still O(mlogn + nlogn) because number of prefix sum queries is O(m) and number of update queries is O(n) and each query is O(logn).
Although it sounds reasonable, could you prove it formally?
I've come up with almost the same idea with you!
Is this a tutorial ?
For problem C,
In the contest, I also used a stack to match the paranthesis first, but then I chose an O(nsqrtn) approach (how stupid) which ultimately got me a TLE. QAQ.
Yes, O(N*sqrt(N)) was too much for this problem (with N being 1 million). But still, it might be an interesting an approach. Can you share it with us?
Sure~
The first part was exactly the same as "First I used a stack in order to match each closing paranthesis to the closest unmatched open paranthesis before it (if any). In the optimal answer for any query, a closing paranthesis is either matched with that open paranthesis or with none (I did not really prove it, but it seems reasonable)." :P
Then sort the queries by "Build sqrt(n) bucket due to the left point, put query [l,r] into (l/sqrt(n)+1)-th bucket, inside each bucket sort the queries by the right point" (also known as Mo Dui's algorithm in Chinese), and then brute-forced through all the queries using two pointers, checking whether a pair of paranthesis was added or deleted.
OK, I got it. So for the current bucket (containing the left endpoints of some queries) you can maintain the number of pairs of parantheses fully contained in buckets to its right (and up to the right endpoint of the current query). Then, you would consider the positions between the left endpoint of the current query and the end of its bucket (or the right endpoint of the query, whichever comes first) to check for possible extra pairs of parantheses starting there and contained in the query interval. At least that's how I would implement it and it would lead to an O(N * sqrt(N)) time complexity : O(N) for each bucket containing left endpoints of some queries, plus O(sqrt(N)) per query. I don't see how you would use the two-pointer algorithm, as the left endpoints of the queries from the current bucket are not also sorted (so you might have to go back and forth with the pointer pointing to the left endpoint of the current query — but that wouldn't be a problem, as this wouldn't amount to more than O(sqrt(N)) per query, anyway).
yes, the point for this algorithm is for the two pointers to go back and forth, but the time compensation would still be O(NsqrtN) ~
anyway, choosing this algorithm in this precise problem just seems a bit going too far... :(
I don't understood DIV2-D problem.Can it be solved with DP?
I know that it has been said already, but it's almost impossible to read this kind of tutorials in English (I mean when it's google translated). I would volunteer to translate the solutions from Russian to English, shouldn't take that much time and effort :)
I really cannot understand Sereja's D1-C solution at all. Could someone explain it? What are really stored in each of the segment tree nodes?
b : number of unused '('
c : number of unused ')'
a : number of "()"
for each interval (l, r) you can match X of '(' in interval (l, mid) with ')' in interval (mid+1, r).
and X = min(number of unused '(' in (l, mid), number of unused ')' in (mid+1, r)).
so for interval (l, r)
a(l, r)= a(l, mid) + a(mid+1, r) + X;
b(l, r)= b(l, mid) + b(mid+1, r)- X;
-X because we used X of them and made X "()".
c(l, r)=c(l, mid) + c(mid+1, r)- X;
in 380C can someone explain how is this case handled with segment tree?
left Node = ( ) ) => a = 2, b = 0, c = 1
right Node = ) ( ) => a = 2, b = 0, c = 1
par Node = ( ) ) ) ( ) => a = 2, b = 0, c = 2
but above explanation will give X = 0, a = 4, b = 0, c = 2
In the parent node, a=4.
a is the longest matching subsequence, not substring
thanks, i was solving the question assuming it to be substring. very bad:(
380C — Sereja and Brackets I think a = a1 + a2 + t
should be a = a1 + a2 + 2*t
Else you can output
2*aat the outputAlso storing
ais not required as it is:length_of_sequence - b - cIn the problem C: 380C — Sereja and Brackets,
It should be a = a1 + a2 + (2)*t instead of a = a1 + a2 + t
Or still: a = a1 + a2 + t, then output 2*a.
I have seen some DP solutions for problem C Sereja and Brackets. Can anyone explain how a DP solution would work?
PS: BTW, the tutorial quality is very poor (at least the English version).
I think the problem author should give his tutorial to somebody who can translate that in English, just similar as preparing problems. Hope there won't be more google translated, unreadable tutorials in the future
380A — Sereja and Prefixes
why can the kth of element, kth can be fit in 64-bit integer ?
Kth can't but size of arr can!
Can the problem Sereja and Brackets be converted into an equal problem of : Given a set or intervals and queries (of type l_i and r_i), find the number of intervals within that range ?
I know this is very old, but it may help someone that's studying: on problem Sereja and Brackets there is a way easier solution. The key observation here is that the closing bracket will be chosen greedly, that is, the last opened bracket can be closed with the first available bracket everytime, yelding the optimal bracket matching for any query. That observation being made, the problems is reduced to counting the matchings inside the interval of the query. I did this by first storing the right side of each query in it's corresponding position and then sweeping the string from left to right, keeping a Fenwick Tree (BIT) for the matchings: when a left bracket finds a closing bracket, I add 1 to the position of the left bracket. When I hit a spot that contains some query end, I answer this query with RSQ(Li,Ri).
Here is the pseudocode:
And here is my AC submission: 7108258
nice solution .
This blog is really helpful for those struggling to understand the editorial for 380C — Sereja and Brackets . Also a great resource to learn Segment Trees.
In Div1C — Sereja and Brackets, what if, instead of a subsequence, a substring is asked? How would we proceed?
I misread the problem and was trying to solve this problem, but couldn't find a very efficient merge function in the segment tree that could solve this problem with the given constraints. I'm curious if there is a way...
u basically kesp track of minimum prefix, and final sum , the minimum should be non negative, and sum should be 0 , which can easily be merged with segment trees and by sum i also mean this, if its an opening bracket u add 1, else u subtract 1
Why my N solution get TLE ?
Looking at the problem Sereja and Brackets it seems it should be solvable using some prefix and suffix sums. With each query in O(1) but how do I prove it is not possible? Can anyone please share some thoughts on this? Basically I want to know what is the bottleneck?
Thank you very much Sereja. But excuse me, where is the tutorial?
hi, can anyone explain me why Im having the wrong answer on test 3? I can't figure it out. here is my code:
void sort(int array[], int size) { int i,j; for(i = 0; i < size — 1; i++) { for(j = 0; j < size — 1 — i; j++) { if(array[j] < array[j+1]) { int temp = array[j]; array[j] = array[j+1]; array[j+1] = temp; } } } }
int main() { int n,i; int sumD = 0, sumS = 0;
scanf("%d", &n); int *arr = (int *)malloc(n * sizeof(int)); for(i = 0; i < n; i++) { scanf("%d", &arr[i]); } sort(arr, n); int k = 0; int m = 1; while(k < n) { sumS += arr[k]; k += 2; } while(m < n) { sumD += arr[m]; m += 2; } printf("%d %d", sumS, sumD); return 0;}
In 380C, I get TLE on test 12; help me, please :
include <bits/stdc++.h>
using namespace std;
struct node { int mo, dg, ca; int l,r; node () { mo = dg = ca=0; l=r = 0; }
}; node operator+(node a, node b) { node t; t.l = a.l; t.r = b.r; t.ca = a.ca + b.ca; int tc; tc = min(a.mo,b.dg); t.ca += 2*tc; t.mo = a.mo — tc + b.mo; t.dg = a.dg + b.dg — tc;
typedef vector tnode; void maketree (tnode &tr, string s, int id, int l, int r) { tr[id].l =l; tr[id].r = r; if (l == r){
if (s[l-1] == '(') tr[id].mo = 1; else if (s[l-1] ==')') tr[id].dg = 1; return; } int m = (l+r)/2; maketree(tr,s,id*2, l,m); maketree(tr,s,id*2+1, m+1,r); tr[id] = tr[id*2] + tr[id*2+1]; return; } node getcap (tnode tr, int id, int u, int v) { node t; if (tr[id].l>v || tr[id].r<u) return t; if (tr[id].l>=u && tr[id].r<=v) return tr[id]; return getcap(tr, id*2, u,v) + getcap(tr, id*2+1,u,v); } int main(int argc, char const *argv[]) { ios_base::sync_with_stdio(false); cin.tie(NULL); // freopen("380c.inp","r", stdin); string s; cin>>s; int q; cin>>q; tnode st(4*s.size()); maketree(st,s,1,1,s.size()); while (q--){ int u,v; cin>>u>>v; node re =getcap(st,1,u,v); cout << re.ca <<endl; } return 0; }