I wrote a post about how to tackle certain problems on numbers using dynamic programming techniques over at Stack Overflow. This includes tasks like
- "Find the sum of integers X with digit sum S, where X <= Y" (Y given)
- "Find the number of palindromic integers between L and R"
- "Enumerate all integers between L and R that only have digits 4 and 7"
- "Find the probability that an integer X uniformly chosen from the range [L,R] has at least 10 common digits with a given number S"
that can all be solved with a very similar idea. Just in case somebody's interested.











Here is another good post
Nice, I didn't know that one :) And you just added an image instead of an hyperlink.
Lol sorry look now!!
niklasb please elaborate your following statement under the heading Compute the number f(Y) of integers X with the property X ≤ Y and X is palindromic :
If we can count the f(Y) with the additional restriction that all numbers X must have the same digit count as Y, then we can solve the original problem as well...
You can just iterate over the number of digits, solve the arising subproblems where the number of digits is fixed and add up all the results.
@niklasb is my this implementation satisfies your explanation for O(n^4). If not, please suggest corrections. Thank you for your time.
Compute the number f(Y) of integers X with the property X ≤ Y and X has the digit sum 60
Your implementation is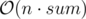 by the looks of it, but only after you add memoization to the
by the looks of it, but only after you add memoization to the
!lobranch as well! I would recommend you not to pass aroundcadas a parameter of typestring, because it might induce unnecessary copying. You could useconst string& cadinstead.This Google query for
"spoj" "numbers between" A and Bgives quite many SPOJ problems of this type.Good observation, I added the query to my Q&A.
There is lecture of Petr on Kharkov winter camps. But on Russian.
Can you give link, please?
link, page 262
Even though it's been a long time since this post was active, can someone help me find an english translation of the document?
Google translate rejects the document as being too huge, and Yandex translate also only translates the first 30 pages. Where can I find the document in English? Or maybe, a translating service capable of translation?
I think you can split needed pages from this pdf file
I am also looking for same(English version of problems) too, let me know if u find the way out.
Google was able to translate the entire document, however lost the formatting. It is hard to read the formulas without proper formatting.
could you please help me in solving : http://www.spoj.com/problems/COOLNUMS/
Here is my solution which takes 0.35 secs only: https://ideone.com/wHAL6j
There are < 1e5 valid digit sequences(at most 10 digits < 4e9). Generate them all. Then simply use concept of digit dp. dp(p,c,w) denotes number of valid numbers whose first upto p digits are generated, c denotes whether the number has become smaller or not than given number N and w denotes digit sequence till now.
can you please explain what did you mean by : "There are < 1e5 valid digit sequences"?
I know this is a stupid ques but please don't mind.
It means given a number x when you sort its non-zero digits you get a sequence of digits. Only this sequence is enough to deduce if digits can be partitioned in 2 subsets or not using subset DP. If you see code I generate all digit sequences at start in 'a' whose size is about 93,000.
thanks mate :)
if possible can you please help me in optimizing this : https://ideone.com/PAVdOT
prob : http://www.spoj.com/problems/NUMTSN/
https://ideone.com/27hw2y
Instead of recalculating the DP each time, you can redefine it as dp(p,c3,c6,c9) = number of p-digit numbers having c3,c6,c9 respective counts of 3,6,9. Then you can preprocess the dp once, and calculate each answer in O(50*17*10) for a single case by just iterating on number of 369's and on the number. Works in 0.03 secs on SPOJ.
"calculate each answer in O(50*17*10) for a single case by just iterating on number of 369's and on the number" can you please explain it a little? I have seen your code but didn't understand the count function.