The last USACO contest, that is, US Open, takes place this weekend. You can start the contest anytime in the 3-day window starting at April 4th.
Well, at least it's not during the next weekend (Crazy Weekend of April 2014, there's one every month :D).
You'll be able to access the contest from the USACO front page. You need to register for an account on the site to compete.
I hope I'll be able to post my solutions again here after the contest ends. I also hope that I'll be able to compete at all, because I'll be who knows where (I certainly don't :D) during the weekend and I wonder if there'll be Internet connection...
Also note that this contest lasts 5 hours, unlike the previous ones. For the same number of problems.
Problems and solutions (just gold so far; post the silver/bronze problems if you have access to them):
Problem 1: Fair Photography.
Given N ≤ 105 integers in range [1, 8] placed on integer points of the x-axis and an integer K ≥ 2, find the longest interval that satisfies the following conditions:
at least K distinct integers occur in the interval,
all integers that do occur in it must occur there an equal number of times.
The interval must start and end at some of the given points. Print the maximum length of such an interval, or -1 if there's none.
Solution
If all integers must occur in the interval, the problem can be solved easily in 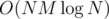 time. This is basically problem ABCSTR of Codechef; read its editorial for further explanation.
time. This is basically problem ABCSTR of Codechef; read its editorial for further explanation.
In this case, however, a subset of integers from the range [1, 8] could occur in the chosen interval. Ok, why not just run the algorithm on all subsets? :D We only need to count the differences as in ABCSTR for integers from the present subset, and we'll remove all entries from the map<> whenever we encounter an integer that's not in that subset — this way, we can make sure that none of these integers can occur in the selected substring. We get complexity 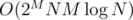 , which isn't particularly great.
, which isn't particularly great.
We can get rid of the logarithmic factor by storing hashes of vector<>s in the unordered_map<> (actually, we can't get rid of it in the contest without coding an entire hash table... shame on USACO for not updating the compiler). A polynomial hash of elements of the vector<>by 2 moduli (109 + 7 and 109 + 9, for example) is strong enough.
We can also get rid of the factor M by updating hashes in O(1). The only 2 updates we need to do are: add 1 to one element of the vector; subtract 1 from all its elements. For polynomial hashes ( of vector A, where the + N is in order to have all terms non-zero and thus remove obvious collisions), these operations correspond to adding pi - 1 and subtracting
of vector A, where the + N is in order to have all terms non-zero and thus remove obvious collisions), these operations correspond to adding pi - 1 and subtracting 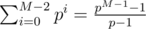 (you don't have to calculate that, just take the difference of hashes of A filled with 1-s and filled with 0-s).
(you don't have to calculate that, just take the difference of hashes of A filled with 1-s and filled with 0-s).
Notice that so far, we can't check if the selected interval actually contains K distinct integers. We can separately calculate for each right endpoint of an interval the largest possible left endpoint for which this condition is satisfied. That can be done by processing points in sorted order and, for each integer, storing its rightmost occurence in a map<>; the rightmost left endpoint is the K-th last of these occurences and can be found by iterating over the map<>. Adding a point only leads to changing 1 entry of the map<>, so this takes 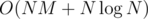 time (the whole algorithm now takes
time (the whole algorithm now takes 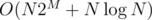 time). Afterwards, we can easily check if some interval contains at least K distinct integers.
time). Afterwards, we can easily check if some interval contains at least K distinct integers.
This leads to a more efficient algorithm. Notice that any point can only be the right endpoint in O(M) different subsets — if you decrease the left endpoint, you can only add integers to the subset, which can be done just O(M) times. The above mentioned algorithm gives us an easy way to compute these subsets, even. Similarly, any point can only be the left endpoint in O(M) different subsets, which can be found by running that same algorithm in the opposite direction.
Let's not try subsets separately, but keep 2M unordered_map<>s, in which we'll store the hashes of vector<>s.
We need a way that allows us to modify hashes quickly — for example, the i-th element of the vector<> is the number of occurences of integer i among the first j points if it isn't in the subset; otherwise, it's the difference between number of occurences of i and of the smallest integer in the subset. Note that when adding integers into the subset, these numbers change, but only all in the subset by the same number c, which makes polynomial hashes rather easy to modify — decreasing all numbers in the subset S by c means decreasing the hash by  , where the sums for all subsets can be pre-computed.
, where the sums for all subsets can be pre-computed.
Try all subsets which have j as the right endpoint and contain at least K elements, in the order in which they go when we move the left endpoint to the left; for each of them, find out if there was some vector<> before that could occur in that subset (was placed in the hash-map of that subset) and was identical to the one we have now — such identical vectors correspond to balanced intervals. Then, add our current vector<> to the hashmaps of all subsets that can have the j + 1-st (think why not j-th) point as their left endpoint.
The resulting complexity is 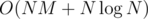 . There are, of course, simpler algorithms where you don't use hashes or clever updates of them at the cost of larger powers of M.
. There are, of course, simpler algorithms where you don't use hashes or clever updates of them at the cost of larger powers of M.
Problem 2
There's a laser placed at point (0, 0) in a plane, shining in the direction of positive y-axis, and N ≤ 105 mirrors (reflecting on both sides) placed at integer points and tilted at 45° to the coordinate axes, that is, as '/' and '\'. The laser beam reflects from these mirrors. You should add one such mirror so that the laser beam passes through a given point (Bx, By). There are also additional restrictions:
the laser beam can't pass through the point (0, 0) again (this condition is satisfied in the initial configuration),
the new mirror can't be placed at the same point as one of the original ones.
It's also guaranteed that the laser beam doesn't pass through (Bx, By) in the initial configuration. Print the number of points at which the new mirror can be placed. Coordinates can be large, up to 109 in absolute value.
Solution
It's obvious that the laser beam will always be parallel to one coordinate axis.
Store the mirrors in every row (equal y-coordinate) in sorted order (by x-coordinate), and in every column (equal x-coordinate) also in sorted order (by y-coordinate). Trace the beam's path by remembering from which point in which direction it went and finding the first mirror in its path, until you find out that it started to loop or went out of bounds.
Trace back the beam's path that could lead to it hitting point 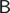 from each of the 4 possible directions. This time, stop when it starts to loop (including hitting point
from each of the 4 possible directions. This time, stop when it starts to loop (including hitting point 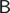 again), goes out of bounds or hits point (0, 0).
again), goes out of bounds or hits point (0, 0).
We've obtained line segments of 2 types — "real" and "desired" and 2 orientations — vertical and horizontal. The new mirror should and can be placed at the intersection of any two segments of both different types and orientations, because we can pick the direction in which it could be placed to tilt the "real" beam by 90° and have it go in the direction of the "imaginary" one into point 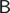 .
.
The problem now reduces to a classic "compute the number of intersections between vertical and horizontal segments". This can be solved by compressing y-coordinates, sorting and sweeplining the segments by the x-coordinate of the larger endpoint. Then, iterate over the vertical segments and remember how many times points covered by horizontal ones; you can calculate the number of horizontal segments that intersect a vertical one using a Fenwick tree. You can keep track of the horizontal segments to add using 2 pointers and of the ones to remove using a map<> of their left endpoints, or just replace each horizontal segment by 2 half-segments which add 1 and -1 to the Fenwick tree.
Time complexity:  .
.
Problem 3
You're given a rooted tree of N ≤ 2·104 vertices. Each vertex can contain a digit from 0 to 9, inclusive. You're also given M ≤ 5·104 rules as pairs (vertex, 5-digit string); string s at vertex x says that if you read the first 5 letters from x (inclusive) to the root, you have to get a string different from s.
The tree is rooted at vertex 1 and vertex i has parent p(i) < i.
Print the number of ways in which you can't assign digits to vertices of the tree (e.g. such that at least 1 of the M rules is broken), modulo 1234567.
Solution
Instead of computing the number of ways in which we can't assign the digits, we'll compute the number of ways in which we can; the answer is then 10N minus that (there are 10N ways to assign digits, in total).
This can be solved by dynamic programming. Let DP[i][j] be the answer for the subtree rooted at vertex i, in case the 4 digits above that vertex are read as j, but this time from top to bottom. There are at most 10 digits we could put in vertex i; for each digit d that we can put there, the number of ways to fill the subtree is the product of DP[x][(10j + d)%10000] over all sons x, because we can fill the subtrees of sons independently and the last 4 digits read on the path from the root to each son will be (10j + d)%10000. Then, DP[i][j] is the sum of these results over all d. We can then find the final answer in DP[1][j] (we can pick any j, it's like creating a path of 4 vertices above the root and choosing the digits in them; there are obviously no rules starting at vertices with depth < 4 below the root, so these digits won't affect anything).
This approach has complexity O(105N) — every edge of the tree is used O(105) times.
We can improve this by noticing that in case all digits are allowed, then the first digit of j (taken as a 4-digit number with leading zeroes) doesn't really matter. In fact, there are just M possible states of DP where it can matter, because each of the M rules forbids one digit d for one state of the DP. So if we calculated 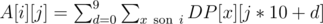 for 3-digit numbers j, then if some state of the DP has all digits allowed, we can immediately say that DP[i][j] = A[i][j%1000]. If a state doesn't have all digits allowed, we can just compute it the same way we did before.
for 3-digit numbers j, then if some state of the DP has all digits allowed, we can immediately say that DP[i][j] = A[i][j%1000]. If a state doesn't have all digits allowed, we can just compute it the same way we did before.
This approach gives a complexity of O(104N + 100M), which I dare say could work in a second or two, because it's just DP, with really just that many operations.
It'd be even better if we could always replace moduling by subtracion if necessary, but we can't, because we need to compute products sometimes, not sums. The large modulus (around 106) also forces us to use 64-bit variables. BTW, this got me thinking about how the Chinese Remainder Theorem can sometimes be useful — if the modulus is composite, we can decompose it into prime powers, compute partial answers modulo each of them and the final answer is just LCM of the partial ones. In this case, 1234567 = 127·9721, which would allow us to use ints, but I doubt it'd be actually helpful.
I don't know USACO's time/memory limits, but I suppose this would still need memory optimization. If the tree was thin enough (there were few vertices in any depth), the DP could be done by decreasing depth, where we'd remember just the answer for states of vertices in the last 2 depths, but I'm not sure what to do in a general case.
UPD: The results are up. Optics and Code have really bad results...











will this contest be rated bronze to silver or silver to gold divisions
Yes!
The last time you just posted the gold soloution here. I'll be glad if you post some hint about silver & bronze here.
I only posted the gold solutions because I had no access to silver/bronze at that time (and forgot afterwards, when the problems were public :D). Yeah, I'll try.
I am responsible for writing some silver analysis for this times OPEN. You can always read my solution after the results come out or ask me for them some time after the contest!
What is the solution for the first problem of Gold division: Fair Photograhy?
I've been trying to edit the blog post for some time, unsuccessfully. It says "404 not found". So far, you can read the editorial of this problem.
Actually I stayed with the solution in
Unable to parse markup [type=CF_TEX]
(where M ≤ 8 is the number of races) explained below, but I fear it will be a bit too slow.Riiight, Latex doesn't work. I'd like to know why...
Yeah, it's too slow. My solution runs in around 3-4 seconds on large inputs (actually, I had a comfortable tool for checking the correctness and time, which I'll elaborate on later), and it's O(N 2^M).
Sorry — multipost.
Sorry — multipost.
The basic idea is like Xellos has mentioned similar to the ABCSTR problem from Codechef.
Checking every 2m subset isn't feasible, but we can prune it by the following observation. Consider cow i with the color ci and maintain a bit mask b = 2ci. If you consider the cows from i to n one by one and perform the bitwise OR operation to your bitmask b by doing bnew = bold | 2cj (where j is the cow you are considering right now) then you will only have just a few interesting subsets. I guess it is at most M - K + 1 for each cow i, where K is the minimum number of types required to be on the picture.
With this observation one can deduce an O(nlogn) algorithm overall.
Actually,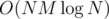 . That's a difference of 8 seconds vs 1 second, so it's not that irrelevant. Or
. That's a difference of 8 seconds vs 1 second, so it's not that irrelevant. Or 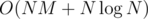 if hash-set is used, I think.
if hash-set is used, I think.
I always leave constants out in the Big O notation since its definition says so. I think your are right yeah, it should be fast enough and runs in less than a second for large input cases.
In this case, it's important to use M as a variable.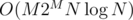 is also
is also  , but the difference is huge.
, but the difference is huge.
Can you please elaborate? Or maybe share your code?
Could you also post solutions for Problem 2 and Problem 3? Thanks!
Yea, working on it. Problem 1 was the most complicated if you wanted the optimal solution and didn't take M for a constant...
nvm
The Latex silliness in CF Markup: if you don't use brackets on the part you want to put in the superscript, it takes the rest of the text, not just the next character.
I corrected it almost instantly, how did you catch it? :D
Results.
Upvoting a blog entry older than 3 weeks is like impossible, in my opinion. I think Codeforces just ignores your upvote. Does anyone know how upvoting system works?
UPD: Yes, it is an off-topic. But I wonder what happens to some blog like this, which deserves lots of upvotes and 3 weeks old (although this blog is 12 days old)? What if Xellos added the editorial after blog is 3 weeks old? Can't I upvote?