Many top accepted solution used DP.I have not practiced DP so much so will wait for editorial then try.I used different approach after the competition and It got accepted.
My Solution for the problem -
I made two cases one for N is even and another for N is odd:
Case 1: N is even.
Calculate N!/((N / 2)!*(N / 2)!).
Divide the above value by 2^N(Multiple of 2 N times) and store it in some double variable.
Multiply the above stored variable with (2*N + 1), this is result, return it.
Case 2: N is odd.
Calculate (N + 1)!/(((N + 1) / 2)!*((N + 1) / 2)!).
Divide the above value by 2^(N + 1) and multiply this value with (N + 1) and store it in some double variable as Sum1.
Calculate (N — 1)!/(((N — 1) / 2)!*((N — 1) / 2)!).
Divide the above value by 2^(N — 1) and multiply this value with N and store it in some double variable as Sum2.
Return this result (sum1 + sum2).
UPD: Sorry I forgot to mention why I posted It.I don't know the proof so can someone give me its proof.











I guess there were many random challenge trials, right? XD
I did not submit it during the contest
My solution's a double DP.
First, compute the probability that a given random walk from position 0 will reach cell j in i steps, without ever moving into negative numbers. Denote this as P0[i][j].
Clearly, P0[0][0] = 1 and P0[0][i > 0] = 0. From state (i, j), we can move to (i + 1, j + 1) with 50% probability and (if j > 0) to (i + 1, j - 1) with 50% probability. Therefore,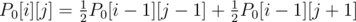 for j > 0 and
for j > 0 and 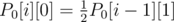 .
.
Now, compute the probability that we'll reach cell j ≥ 0 in step i for the first time: P[i][j]. Clearly, P[0][0] = 1 and P0[0][i > 0] = 0. For i > 0, we can reach cell j - 1 in step k < i for the first time; we also reach it in step i - 1 and between these steps, we move in the same way as computed in P0[i - 1 - k][0]; in step i, the choice is "move right". The probability of these events is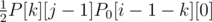 .
.
We can try all k and compute P[i][j] as a sum of all their probabilities. The answer is then the sum of all P[i][j] — each state describes the probability of coloring of one cell in some step. This DP has complexity O(N3), which easily passes a 2s time limit.
Thanks for DP solution.Nice editorial to understand.
Btw my solution is O(N).Can you prove it?
If you use doubles, it's quite obvious that all expressions only require O(N) time to compute. (you do just O(N) multiplications)
No I am not saying to prove its O(N) sorry for misunderstanding.I am asking for proof of my solution , why it is working in this problem.I just wrote the solution on the basis that robot will start moving from origin then what is the probability of reaching origin again if it moves left or right with equal probability.For even N its understandable it will move equal half in both direction but for odd N I used it randomly and its working.
Oh, OK. Rather than "prove", the question's to "compute" the sums from some DP and show that we get your formulas.