416A - Guess a number!
Let's use the usual Div 2 problem A approach — the naive one. We will track the interval which might contain the number we're guessing. With each of the query we update this interval. If at the end the interval is non-empty then we output any number from it, otherwise the result is "Impossible".
Submission: 6606892
416B - Art Union
All we need is to iterate over all painters and for each painter to iterate over all pictures. In the inner loop we also remember when the painter finished working on the picture to make sure that the next painter will not start working on it earlier.
Submission: 6606994
416C - Booking System
Let's solve this one greedy. All we need to notice is that the optimal solution will be to place first the groups with biggest sum which they are ready to pay. For each such group it will be optimal to allocate the smallest matching table. The input limits allow to do a full search when looking for a table.
Submission: 6617198
416D - Population Size
One thing to notice for this problem is that if we cover some interval with a progression then it will better (at least no worse) to include as many elements to the right of it as possible. So the solution is to greedy — find the leftmost number not covered by a progression, start a new progression with that number (the interval covered by that progression will be of size 1) and then try to extend this interval to the right as far as possible. Repeat this step until all the numbers are covered. One thing you should pay attention to is which numbers can be covered by one arithmetic progression, for example:
If there are no fixed numbers in the interval then we can cover it with one progression.
If there is only one non-fixed number in the interval then we can cover this interval with one progression.
If there are more than one non-fixed numbers in the interval then we can calculate the parameters of the progression (start value and difference). All non-fixed numbers should match those parameters. Difference should be integer.
If the progression is ascending and there are some non-fixed numbers in the beginning then those numbers should match positive numbers in the progression.
Same way if the progression is descending then we can include numbers from the right side only while matching progression term is positive.
Submission: 6607174
416E - President's Path
Let's look at the graph given to us in the example:
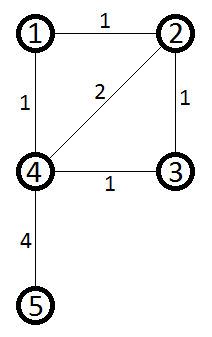
We need to count the count of the edges on all the shortest paths between each pair of vertices. Let's do something easier first — instead of counting all the edges we will count only those which have the destination vertex on its side. For example here are the edges belonging to shortest paths from 4 to 2 which are connected to vertex 2:
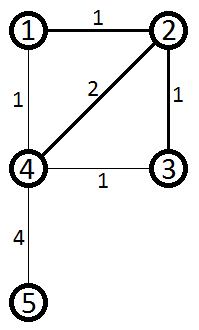
Let's denote this number like this: inEdgessource, v — number of edges which go into vertex v on some shortest path from source to v. In the given example inEdges4, 2 = 3. Let's also denote the set Ssource, dest — it is a set of the vertices which belong to at least one shortest path from source to dest. For example S4, 2 = {1, 2, 3, 4}. With these two variables it can be seen that the answer for vertices source and dest will be:

In other words the answer for vertices s and d will be equal to the sum of inEdgess, v for all vertices v, which belong to any shortest path from s to d. So the only thing left is to calculate these S and inEdges. Both of them can be easily calculated if you have minimum distances between all pairs of vertices. And these distances can be calculated using the Floyd-Warshall. So the full solution is:
Calculate minimum distances between all pairs of vertices using Floyd-Warshall algorithm.
Count inEdges. Simply iterate over all source vertices and all edges. For each edge check whether any of its ends belong to any shortest path from source.
Calculate the answer. Let's have three loops to iterate over the vertices — — source, destination и mid. First two vertices are those for which we're calculating the answer. Third vertex is the vertex which should belong to any shortest path (basically we're checking whether v belongs to Ssource, dest). If mid belongs to any shortest path from source to dest then we add inEdgessource, mid to the answer.
Each step has a complexity O(n3).
Submission: 6607257
P.S.: Please feel free to let me know about any typos, errors, etc using the private messages.











please explain this test case for problem D
5 -1 -1 1 -1 -1
the accepted solutions prints 1 where the problem statements says "Values -1 may correspond to an arbitrary positive integer and the values ai > 0 must be equal to the corresponding elements of sought consecutive record of the progressions.".
can you tell me the expected progression for this case.
The progression in this case would be: 1 1 1 1 1. It is allowed to have a progression with step equal to 0.
416C — Booking System : how dp can be applied ? a hint ?
Something like the classical LCS -Longest Common subsequence- problem.
If the ith group can set on the jth table, then we try to seat them taking the benefit or to decide not to seat this group. else we pass the jth table going to the (j+1)th one.
Make sure to sort the two arrays of the input.
Hi, thanks for the hint,but I am not able to understand it completely, can you elabortate please,I am a beginner, Thanks! :)