450A - Jzzhu and Children
You can simply simulate it or find the last maximum ceil(ai / m).
450B - Jzzhu and Sequences
We can easily find that every 6 numbers are the same. It's like {x, y, y - x, - x, - y, x - y, x, y, y - x, ...}.
449A - Jzzhu and Chocolate / 450C - Jzzhu and Chocolate
We assume that n ≤ m (if n > m, we can simply swap n and m).
If we finally cut the chocolate into x rows and y columns (1 ≤ x ≤ n, 1 ≤ y ≤ m, x + y = k + 2), we should maximize the narrowest row and maximize the narrowest column, so the answer will be floor(n / x) * floor(m / y).
There are two algorithms to find the optimal (x, y).
Notice that if x * y is smaller, the answer usually will be better. Then we can find that if k < n, the optimal (x, y) can only be {x = 1, y = k + 1} or {x = k + 1, y = 1}. If n ≤ k < m, the optimal (x, y) can only be {x = 1, y = k + 1}. If m ≤ k ≤ n + m - 2, the optimal (x, y) can only be {x = k + 2 - m, y = m}, because let t = m - n, n / (k + 2 - m) ≥ (n + t) / (k + 2 - m + t) ≥ 1.
floor(n / x) has at most
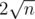 values, so we can enum it and choose the maximum x for each value.
values, so we can enum it and choose the maximum x for each value.
449B - Jzzhu and Cities / 450D - Jzzhu and Cities
We consider a train route (1, v) as an undirected deletable edge (1, v).
Let dist(u) be the shortest path between 1 and u. We add all of the edges (u, v) weighted w where dist(u) + w = dist(v) into a new directed graph.
A deletable edge (1, v) can be deleted only if it isn't in the new graph or the in-degree of v in the new graph is more than 1, because the connectivity of the new graph won't be changed after deleting these edges. Notice that you should subtract one from the in-degree of v after you delete an edge (1, v).
449C - Jzzhu and Apples / 450E - Jzzhu and Apples
Firstly, we should notice that 1 and the primes larger than N / 2 can not be matched anyway, so we ignore these numbers.
Let's consider each prime P where 2 < P ≤ N / 2. For each prime P, we find all of the numbers which are unmatched and have a divisor P. Let M be the count of those numbers we found. If M is even, then we can match those numbers perfectly. Otherwise, we throw the number 2P and the remaining numbers can be matched perfectly.
Finally, only even numbers may be unmatched and we can match them in any way.
449D - Jzzhu and Numbers
Firstly, we can use inclusion-exclusion principle in this problem. Let f(x) be the count of number i where Ai&x = x. Let g(x) be the number of 1 in the binary respresentation of x. Then the answer equals to 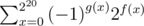 .
.
Now the task is to calculate f(x) for every integer x between 0 and 220. Let fk(x) be the count of number i where Y0&X0 = X0 and X1 = Y1 (they are defined below).
We divide x and Ai into two parts, the first k binary bits and the other 20 - k binary bits. Let X0 be the first part of x and X1 be the second part of x. Let Y0 be the first part of Ai and Y1 be the second part of Ai.
We can calculate fk(x) in O(1):
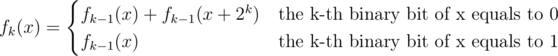
The problem can be solved in O(n * 2n) now (n = 20 in this problem).
449E - Jzzhu and Squares
Consider there is only one query.

Let me descripe the picture above.
A grid-square can be exactly contained by a bigger square which coincide with grid lines. Let L be the length of a side of the bigger square. Let i be the minimum distance between a vertice of the grid-square and a vertice of the bigger square. Let f(L, i) be the number of cells which are fully contained by the grid-square.
We can divide a grid-square into four right triangles and a center square. For each right triangle, the number of cells which are crossed by an edge of the triangle is L - gcd(i, L). Then, the number of cells which are fully contained by the triangle is [i(L - i) - L + gcd(i, L)] / 2.
f(L, i) = (L - 2i)2 + 2[i(L - i) - L + gcd(i, L)] = L2 - 2iL + 2i2 - 2L + 2gcd(i, L)
Firstly, we enum L from 1 to min(N, M). Then the task is to calculate 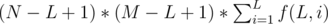 .
. 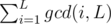 can be calculated by the following steps:
can be calculated by the following steps:
Enum all of the divisor k of L and the task is to calculate the count of i where gcd(i, L) = k.
The count of i where gcd(i, L) = k equals to φ(L / k).
Finally, 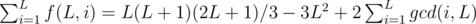 .
.
If there are multiple queries, we can calculate the prefix sum of 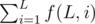 ,
, 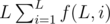 and
and 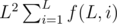 , then we can answer each query in O(1).
, then we can answer each query in O(1).










The picture of div1E failed...
Can you see it now?
yes. Thanks.
failed again?
(450 B) We can easily find ... !!!!, lol. It is tricky. I spent all my time trying to find the solution using Matrix Exponentiation.
Actually, you would have to notice, through the recursive definition, that for any n > 2, the number Fi = Fi-1 — Fi-2.
you start with x | y then the third would be y-x
x | y | y-x then the fourth is y-x-y=-x
x | y | y-x | -x then the fifth is -x-y+x=-y
x | y | y-x | -x | -y then the sixth is x-y
x | y | y-x | -x | -y | x-y then the seventh is x-y+y=x
x | y | y-x | -x | -y | x-y | x then the eighth is x-x+y=y
x | y | y-x | -x | -y | x-y | x | y and we have a cycle
so you would have to choose an answer depending on n modulo 6.
I agree, the explanation lacks some insight, I didn't understand the solution for div 2 D.
Thanks, it is a nice solution.
I put an alternative explanation, in more perspective of Math, on why we have a cycle of 6. And yes, it was bugging me so much, so I decide to review my textbook write something about it :)
Do we have some reasoning why Jzzhu and Apples solution is always correct ?
By the algorithm, all numbers except 1 and prime P > n / 2 (and maybe one left) get matched. And that's the maximum number of match.
yeah, but how do you ensure that all the remaining numbers of the form 2P can be matched?, i mean why this quantity (the remaining numbers) is always an even number (for match all these), i mean it might be that one number get unmatched from all these
Yes, just let this number unmatched.(The quantity isn't always even!)
yes, but then we need a proof to say that this is maximum, because ysymyth told that all numbers are matched (i refer to all numbers but 1 and primes larger than N/2)
Well, if it is even, so all numbers are matched. If it is odd, necessarily at least one number must be discarded and the strategy discards only one number, so it's also maximum.
thanks
Also remember that the discarded number is always even, this way we make sure that at most one number is discarded for every prime and that every discarded number can be paired with every other discarded number.
So in the end we match all multipliers of a prime not yet matched and if we must discard a number we know that number will not be a waste.
Among the discarded numbers all can be matched, this leaves at most one unmatched discarded number at the end (in this case, every other discarded number has been matched).
This strategy is the best because if we must discard a number when looking among the multiples of a certain prime it makes sure that it can be matched in the end and won't be a waste, if it must be a waste it will be the only waste.
Can anybody help me on 450D — Jzzhu and Cities, I think my algorithm can work,I use spfa to record which edge update the dist, and finally if it is not this train update the final dist,I can delete the train.But got TLE on 30..Can not understand why.7182221
maybe you can try "slf"
slf??What's that mean?
You can also use Dijkstra
I know..But I don't know why I got TLE.
I heard someone hacked by using special data.It makes spfa TLE.You know,when hack succeed the data will be added to test.Sorry for my poor English.XD
But I think this algorithm works well..I mean time complexity is alomost O(n).
According to Wikipedia, "For a random graph, the empirical average time complexity is O(|E|)"
One can make SPFA works very slow with a special graph.
"Empirical complexity" always make me laugh :P.
if dijkistra gives TLE.
if SPFA was hacked.
if bellman Ford gives TLE.
How to solve 449B
use ajency list, not matrix, then you do not get timelimit
What I use is adjacent list not matrix...
If spfa means shortest path faster algorithm, that isn't linear... is O(k*|E|), which worst case is O(|V|*|E|), if I'm not wrong.
For 450E I wrote almost correct code(#1 submission in Div2) except I chose the one number to discard(for each P) between a couple of high numbers instead of 2P and got exactly one pair missing in Test #12.. :P Submission in Py2
The last equation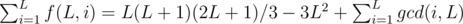 seems wrong. "gcd(i,L)" should be "2*gcd(i,L)".
seems wrong. "gcd(i,L)" should be "2*gcd(i,L)".
Thanks.
DIV1.B “A deletable edge (1, v) can be deleted only if it isn't in the new graph or the in-degree of v in the new graph is more than 1,”
you should output "2", but the right answer should be "1". Did I misunderstand that?
When you delete an edge, you should also delete it in the new graph, so the in-degree of 2 in the new graph is 1 when you are deleting the second deletable edge (1, 2).
In this contest when i tried to open codeforces.com I directed to some other site which has same name as codeforces.com but it contain some information about management,health insurance and some other irrelevant thing. It happen with me often and it only happen during contest and waste my valuable time during contest. This problem reside for some time and automatically resolve. Any solution,,,??
Please can you post a more detailed analysis for div2 D ?
1)"We add all of the edges (u, v) weighted w where dist(u) + w = dist(v) into a new directed graph." I don't undestand it. It would be nice if there was an example.
2)Can somebody help me optimize my algo or say that it's wrong?
Can someone please take his time to explain problem C div2. The editorial is just meaningless. And thank you.
how can you say it's meaningless? it explains everything you need to know...
But if you still think it's too hard to understand the editorial, focus on the 2nd way of solving it, as it's simpler to understand: Let x be the number of times you'll divide a row or a column. you just have to go through all the values of x: from 1 to and from 1 to
and from 1 to 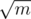 to see which gives the highest answer, because there are only
to see which gives the highest answer, because there are only 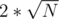 different divisors of any number N. So if you check, at each step, the answer for the following cases:
different divisors of any number N. So if you check, at each step, the answer for the following cases:
(m / x) * (n / (k - x + 2)) // do x = m/x and recheck (m / x) * (n / (k - x + 2))
(m / (k - x + 2)) * (n / x) do y = n/y and recheck (m / (k - x + 2)) * (n / x)
Just watch out for corner cases that can give you a wrong answer (x > K+1 or x <= 0).
Could not understand Div2 D. Someone please explain.
Solution is not very difficult. We can solve this problem by using Deikstra's algorithm with heap:
0) array dist[n] — dist[i] is the value of the shortest path to city i from capital
1) Dist[1] = 0 — 1 is a capital from statement. Then we should update all distances by using railways, mark "true" for ich city that it was improved by railway in some boolean array ( for example ok[n] ).
2) Forget about railways and start Deikstra's algorithm with heap. Add all dist[i]!=+inf in a heap and than try to improve our distances by usual roads. But there are some tricks. We should set ok[i]=false in two cases:
We have an road from v to u with weight s. We try to improve dist[u].
a) dist[v]+s<dist[u] — this means that using railway is bad as the distance with using railway is bigger.
b) dist[v]+s==dist[u] — this means that it doesn't matter to use the railway or to use the road. So we don't need in a railway and we can destroy it.
3) After finishing the Deikstra's algorithm. Calculate the nomber of ok[i]==true. (K — count) will be the answer. 7188851
Why the output of the Div-2 D is 2 for the following Input:: Input ::
5 5 3 1 2 1 2 3 2 1 3 3 3 4 4 1 5 5 3 1 4 5 5 5
In div 2 problem C editorial, it is mentioned that floor(n/x) can have at most 2*sqrt(n) values can anyone explain it? But according to me x can go from 1 to n, so the total values of floor(n/x) can go from 1 to n .
Can somebody help me with problem B of Div 1. I implement the solution of editorial but i get WA on test 5 and i can't debug the code. I think it's absurd. Here is the code: My submission
I found the problem . I subtract one from the in_degree of the vertex when the edge wasn't in the new graph. Here is AC code:http://codeforces.com/contest/450/submission/7193321
Sorry, wrong idea
I think a simpler way to approach div.2 D/ div.1 B is not by creating a new graph.
One can run Dijkstra's algorithm on the graph single-sourced from node 1, where the heap will store (and sort by in order) : current distance, is train track, and current node. This would guarantee that all the optimum paths without using a train track will be processed first.
After that, we compare the given train tracks to the shortest path and delete off as much as we can.
My practice submission link: http://codeforces.com/contest/450/submission/7197600
Your idea is awesome and the implementation is also beautiful :D
For Div1B my approach (Wrong answer):
Use Dijkstra. Equal distances are compared on the type of edge. That is, if we can reach somewhere via a road, and some other place via a train route, traversing the same distance, then the road is selected before the train. This is done by assigning a type 0 to roads, and 1 to train routes. Thus, train routes are processed only when necessary.
Next, I make a
setof train edges. We know when a edge is permanent in Dijkstra, when a vertex is popped out of thepriority_queue. We can save the edge type, while insertion is done into thepriority_queue. Now, if an edge of type1is popped out, then we know that this train route is used in the graph, therefore, it is removed from theset.In the end, the size of the said
setis returned.My submission
Your modified code (to check my Dijkstra, which seems correctly implemented)
Hi, can u explain use of tot[] in your code using an example? Also, is there a case possible where d<=dist[a] but used[a]=1 ? bboy_drain
Can you explain in more details please?
Check out my blog for a well commented and named code: https://codeforces.com/blog/entry/128562
can you offer the offical source code of the question?thanks
Can anyone explain the formula in Div1-D solution ?
About its meaning and writing :)
You can look at my code if it helps . I have done exactly according to the editorial.
Sorry I wanted to mean "How can i write this formula to a blog or a comment ?". Anyway, actually i want to learn explanation of the formula. Sorry for bad English.
The numbers of i where Ai&x = x is f(x)
so if you pick from these f(x) numbers
you will get 2^f(x)-1 groups
whose result y will satisfy y&x = x
and it's clear that y has same or more bit to be 1 compare to x
Its clear that groups whose result have at least 0 bit to be 1
will contain all groups whose result is 0
so we add it to our answer
but it also contains some groups whose result has some bits to be 1
so we minus those groups which have at least one 1
but then we will minus too many times for groups have two or more bits to be 1
so we should add them back
but for those have three we add them too much ...
so we just keep add back and minus back
until the numbers of bit is too many for Ai in this case is 20
sorry for poor English
For 449D-Jzzhu and Numbers
I think in the formula after the sigma should be (-1)^g(x)*(2^f(x)-1)
since you have to choose a number at least
May be you are correct. But the answer won't change.
zyh could you pls explain , how this formula come
My friend make problem E into noip practice.
You have a good friend. :)
I implemented Jzzhu and Cities like this, but I've got WA on test 5. What's my mistake?
The picture of div1E failed...
The picture of 449D failed.
Like this:
Then the answer equals to
Unable to parse markup [type=CF_TEX]
in Div2 C, how is the answer floor(n/x) * floor(m/y)...
How this floor(n/x) came into picture?
Could someone please explain.
Thanks :)
To maximize dimension of pieces, we must divide choco such that row and col of each piece nearly equal. So we divide n to x choco rows and m to y cols, and take floor because of minimum area
Can I use ternary search (on number of horizontal(vertical) cuts for problem C div 2 ?
you need to minimize the denominator not maximize, i blindly coded ternary search without thinking and then regretted it. :/
Sorry, I made a mistake.
You are right.
In div1, please anyone explain me why for each right triangle, the number of cells which are crossed by an edge of the triangle is L - gcd(i, L) ?
In Div1 D, how to use inclusion exclusion to get the answer as
The total number of possible sets with given n numbers is (2^n — 1). Now, we need to remove sets which have at least one bit set after the & operation of all elements. That is why we subtract 2^f(x) for 1,2,4 etc. But, we have over subtracted the sets which end up with two bits set i.e., subtracted them twice (or more). We need to add them up, hence adding everything with at least 2 bits set. This is regular inclusion exclusion.
raja1999 could you pls explain me as well ,how to get this formulla
The idea of Div2 D/ Div1 B given in the editorial is very abstract. Here is how I solved the problem. Firstly add all the roads to the graph, then add all the routes one by one removing the routes which go towards the same city but have a larger weight(longer distance). In this process we may even end up removing some of the roads as well which have a larger weight (this won't affect the answer), so we need to be careful while incrementing the count of removed routes. After this run Dijkstra's algo to find shortest path distances of all cities from the capital. After this for all the routes that still are not removed, iterate over them one by one and for every train route that goes to city v, check to see if the train route has a greater length than the shortest dist to v. If it does, simply remove it and increment count, otherwise if it has an equal length to the shortest dist, try to see if an alternate path can be found to city v that has the same length. For this, iterate over all neighbors of v(not including the capital) and check to see if (shortest dist. to u) + (weight of edge {u, v}) == shortest dist. to v(or the route length). If this condition holds true for some vertex v != the capital, then we can remove the train route and increment count. Since we need to perform deletion operations on the edges, the adjacency list can be implemented as an array of sets of pairs of (neighbor index, weight). Here is the implementation.
Actually you don't need to erase something when implementing see my code 97940629
Please explain 449D. I really can't get my head around the inclusion and exclusion explanation.
What is wrong with this solution for Jzzhu and Cities? Please help me.
Here is my solution for 449B: 117809879
It follows what the editorial says but with two tricks:
d[u] + len == d[v]); and if you find a shorter path, resetp[v]to 1.if (d[v] != INF) q.erase({d[v], v});), otherwise you will get TLE (117809032)209956322
Div2 C, Here is the second solution that was mentioned in the Editorial.