Given an array where each element represents a stick length, how many triangles can be formed choosing 3 different elements?
I know O(N^2) solution, is there a faster solution for this problem?
Thanks.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 7 | SecondThread | 150 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Given an array where each element represents a stick length, how many triangles can be formed choosing 3 different elements?
I know O(N^2) solution, is there a faster solution for this problem?
Thanks.
| Name |
|---|



I'd wager it's at least as hard as http://en.wikipedia.org/wiki/3SUM, so probably not.
Thanks, I'm having trouble to solve a problem who basically asks: Given a set of sticks (at most 10^5) whats the probability to choose 3 different sticks whose form a triangle.
I suppose it have a trick.
Can you provide a link to that problem? :)
acm.tju.edu.cn/toj/showp4004.html
Warning: I don't know if it really works, it's just an idea, tell me if I'm wrong :)
First of all we have to sort the array. We will count the number of bad triangles. A bad triangle is defined as a tuple (i, j, k), with i < j < k and L[i] + L[j] < = L[k] (where L[i] = length of the i-th stick). We notice that the maximum sum for L[i] + L[j] is 106.
Let's note Ways[S] — the number of ways to express S as a sum of two numbers from the array, Freq[S] — the frequency of S in the array, Count[S] — how many numbers greater than or equal to S are in the array. With these notations, the answer can be expressed as the sum of Ways[S] * Count[S], for each possible S.
Now, how to find Ways[]: let's build two polynomials:
P = Freq[0] * X0 + Freq[1] * X1 + ... + Freq[VALMAX] * XVALMAX
Q = P2
Now, we can get the formula:
Ways[S] = (Coef[S] - Freq[S / 2]) / 2, if S is even
Ways[S] = Coef[S] / 2, if S is odd
where Coef[S] = the coefficient of xS in Q.
If S is even, from the total number of possible pairs, we should subtract those pairs which use the same element. After that, divide by 2 to obtain the number of ordered pairs (in terms of i and j from above) with sum S (if you don't want to have only ordered pairs, you should skip the division by 2).
Q can be obtained using FFT in O(VlogV), where V is the maximum sum of two elements from array, in our case 106 (but I think we can consider V = 105, because any sum greater than 105 can form only good triangles)
The final time complexity is O(T * (VALMAXlogVALMAX + NlogN))
I say again, I don't know if it works :)
yes, it works. I had a similar idea and got AC.
This goes to show that actually providing the problem is important, instead of an incomplete summary. Without the fact that the stick lengths are at most 105, you can't do better than O(n2).
what is you O(N^2) solution?. I've got O(N^2loglogN) one.
Is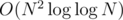 using van Emde Boas tree? If so, it'd be
using van Emde Boas tree? If so, it'd be 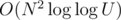 , where U is the maximal value of an element you want to insert to the tree.
, where U is the maximal value of an element you want to insert to the tree.
If you want O(N2), you should use three pointers method. The code would look like this:
P.S. Beware of bugs in the above code; I have only proved it correct, not tried it. Donald Knuth
what is your proof than the while loops operates in O(1)? because i'm not convinced
the n^2loglogn is hard to explain but I'll try. first a n^2logn solution: I use the fact that if I have pointers i,j,k such that i<j<k which is a valid triangle than than for all f, j<f<k : i,j,f is valid triangle. now for the loglogn part: for each i(constant) : I find the 'k' for the triple i,i+1,k than i will take a new k* equal to (n-k)/2 and search the new j* for the triple i,j*,k* now note that for each i<j<j* I only need to search the 'k' in the subarray[k,k*] and for each j*<j<n-1 I only need to search the 'k' in the subarray [k*,n-1] I use Divide and conquer on those subarrays. eventually for constant i, finding for each j, how many triplets will take nloglogn, looping thorugh all i we get n^loglogn.
No, your first solution is O(N3) and second is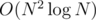 . I won't explain why, since reading a book about alogrithm analysis will be better for you.
. I won't explain why, since reading a book about alogrithm analysis will be better for you.
My while loop doesn't work in O(1), but if you will take the body of the outer
forloop, it'll work in O(N). It's so just because it's impossible to decrease k more than N - 2 times.my first solution is O(n^2logn) while I'm now having trouble finding the tiem complexity of the second one.
I reread your code and now I understand it.
It's really simple, actually. First, sort the array; then iterate over the middle stick j. For fixed j, you can find the sums ai + aj for all i < j, which are already sorted, and for each k > j, count how many of them are > ak, which can be done with 2 pointers in O(N) time.
AlexanderBolshakov post the solution, if you want, you can read in more details here: https://codility.com/media/train/13-CaterpillarMethod.pdf
This is a question same as yours : http://www.codechef.com/problems/NOTATRI .As xellos said N logN for sorting and O(N) for checking for each N.
EDIT: Just saw my idea was the same as SealView and his post is better explained (see here)
I had this idea:
Define F(x) = Σ (ni * xi) and F2(x) = Σ (ni * xi * 2), where i is the value from the array and ni is its frequency. Then P(x) = (F(x)2 - F2(x)) / 2 will store the sums of combination of two items from the array, along with it's frequency. I then build an array M, storing the suffix sum from the factors of P(X).
To calculate I do the following: let vi be the value of the i-th value in array (ordered decreasingly). I iterate those values, fixing it as the biggest value in a combination. The amount of combinations with the sum of the lowest values greater than vi is m[vi + 1] minus the amount of sums where one of the values is greater than vi and minus triples that have been processed already. After calculating the amount of valid triples with vi as it's biggest value, we store a correction variable, so as to remove the pairs where vi appears from the result in the next iteration. This assures that for any i, the answer will have only pairs with single values smaller than vi. This is the tricky part actually, finding the right formulas.
Finding P(X) efficiently is crucial, since all other steps (other than sorting the values) are O(n), so I use FFT to calculate P(x) in O(n * log(n)). The overall complexity is O(n * log(n)).
After fixing the formulas for erasing invalid/processed pairs and using a struct instead of C++'s standard complex implementation, I got AC'd.