A. This problem can be easily solved with the following algorithm. First, read names ans statuses of all crew members into an array. Next, iterate over the entire array 4 times. In the first pass output names of rats. In the second pass output names of women and children. In the third pass output names of men. Finally, in the fourth pass output the name of the captain.
B. In this problem you can simulate the process of soliders training
until there is at least one soldier with rank less than k. We iterate over the array of ranks and increase by one the ranks of every soldier who is the last in his group (if he has the rank less than k, of course). This operation preserves non-decreasing order of the ranks. Obviously we will need no more than kn trains. So we have O(kn2) solution. It fits the limits.
You can prove that we will make no more than n + k trains in the solution above. Therefore it really works in O(n(n + k)). In addition there is an O(n) solution.
C. Consider all of the numbers which the thinker may thinks of. Next we select from them ones which fit all thinker's answers. If there is exactly one such number, output it. If there are no such numbers, output "Incorrect data". Otherwise output "Need more data". The complexity of this solution is O(104 × n).
Most of mistakes in this problem were caused by leading zeros. Either while printing the answer or while transforming numbers into strings for checking them.
D. Main idea of the solution is walk the island around with a "snake". You can do it, for example, this way:
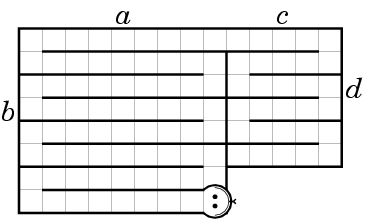
or this way:
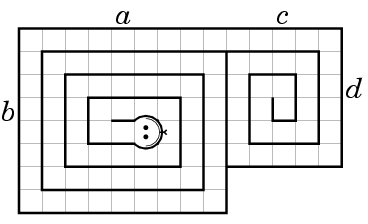
Then we can just "cut" the snake into the pieces of appropriate length. It is clear that all the resulting figures will be connected.
The complexity of this solution is O(max(B, D) × (A + C)).
E. Define a state as some layout of sweets in a box. We have to detrmine for every state whether it is winning or losing. The state is winning if you can do a acceptable move to a losing state. Otherwise it is losing. For example, the state corresponding to the empty box is losing because there are no moves from this state. A state corresponding to a box containing only one candy is winning because there is a move leading to a losing state - eating the candy leaves the box empty.
Thus, if the state given in the input is winning the answer is "Karlsson", otherwise answer is "Lillebror".
It's useful to represent a state with a 19-bit mask where the i-th bit is 1 if there is a candy in the i-th cell. Similarly, each move can be respresented
with a mask where the i-th bit is 1 if the candy in the i-th cell is to be eaten during the move.
Note that a move move can be done in a state mask if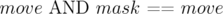 , and doing this move leads to the state
, and doing this move leads to the state 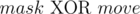 . Also note that in this case
. Also note that in this case 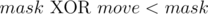 .
.
These observations lead to the following solution: iterate over every state from 0 to 219 - 1. For each state examine the list of possible moves and find ones that can be done in the current state. Assuming that we know the winningness of the states with lesser numbers, we can determine the winningness of the current state as described above.
It's convenient to precompute the masks for all possible moves and store them in an array. This is apparently the most tricky part of this problem with lots of approaches ranging from the explicit enumeration to long intricate functions producing the moves list. Any approach will do, provided it is carefully implemented.
The complexity of this solution is O(219k), where k is the number of different moves (which turns out to be equal to 103).
UPD. I have rewritten this tutorial with some tips by a guy who knows English much better than me :)
B. In this problem you can simulate the process of soliders training
until there is at least one soldier with rank less than k. We iterate over the array of ranks and increase by one the ranks of every soldier who is the last in his group (if he has the rank less than k, of course). This operation preserves non-decreasing order of the ranks. Obviously we will need no more than kn trains. So we have O(kn2) solution. It fits the limits.
You can prove that we will make no more than n + k trains in the solution above. Therefore it really works in O(n(n + k)). In addition there is an O(n) solution.
C. Consider all of the numbers which the thinker may thinks of. Next we select from them ones which fit all thinker's answers. If there is exactly one such number, output it. If there are no such numbers, output "Incorrect data". Otherwise output "Need more data". The complexity of this solution is O(104 × n).
Most of mistakes in this problem were caused by leading zeros. Either while printing the answer or while transforming numbers into strings for checking them.
D. Main idea of the solution is walk the island around with a "snake". You can do it, for example, this way:

or this way:

Then we can just "cut" the snake into the pieces of appropriate length. It is clear that all the resulting figures will be connected.
The complexity of this solution is O(max(B, D) × (A + C)).
E. Define a state as some layout of sweets in a box. We have to detrmine for every state whether it is winning or losing. The state is winning if you can do a acceptable move to a losing state. Otherwise it is losing. For example, the state corresponding to the empty box is losing because there are no moves from this state. A state corresponding to a box containing only one candy is winning because there is a move leading to a losing state - eating the candy leaves the box empty.
Thus, if the state given in the input is winning the answer is "Karlsson", otherwise answer is "Lillebror".
It's useful to represent a state with a 19-bit mask where the i-th bit is 1 if there is a candy in the i-th cell. Similarly, each move can be respresented
with a mask where the i-th bit is 1 if the candy in the i-th cell is to be eaten during the move.
Note that a move move can be done in a state mask if
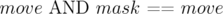 , and doing this move leads to the state
, and doing this move leads to the state 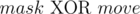 . Also note that in this case
. Also note that in this case 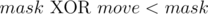 .
.These observations lead to the following solution: iterate over every state from 0 to 219 - 1. For each state examine the list of possible moves and find ones that can be done in the current state. Assuming that we know the winningness of the states with lesser numbers, we can determine the winningness of the current state as described above.
It's convenient to precompute the masks for all possible moves and store them in an array. This is apparently the most tricky part of this problem with lots of approaches ranging from the explicit enumeration to long intricate functions producing the moves list. Any approach will do, provided it is carefully implemented.
The complexity of this solution is O(219k), where k is the number of different moves (which turns out to be equal to 103).
UPD. I have rewritten this tutorial with some tips by a guy who knows English much better than me :)









 +4
+4


