
Всем привет!
Cегодня (23 ноября) в 12:00 пройдет очередная командная интернет-олимпиада для школьников. Уже через неделю мы вас ждем на ВКОШПе, а пока можно еще раз потренироваться. На этот раз тренироваться вы будете с Физруком.
Продолжительность — 3 часа в базовой номинации, 5 часов — в усложненной. Подробнее о номинациях и правилах можно прочитать здесь.
Если вы еще не регистрировали команду на интернет-олимпиады в этом сезоне, то сделать это можно тут.
Условия появятся на сайте в момент начала олимпиады. Сдавать задачи можно в PCMS2 Web Client (русская версия).
Олимпиаду подготовили Дмитрий Филиппов (DimaPhil), Илья Збань (izban), Евгений Замятин (Odeen), Захар Войт(zakharvoit), Григорий Шовкопляс (GShark) и Илья Пересадин (pva701).
Удачи!











Огромное спасибо авторам за очень хороший контест!
Очень понравилась задача L. Интересует такой вопрос: можно ли получить AC решением с асимптотикой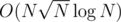 ?
?
вряд ли, вообще предполагалось решение за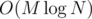 . одна команда сдала ее за
. одна команда сдала ее за 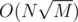 , это решение едва уложилось в тл.
, это решение едва уложилось в тл.
А как за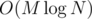 ?
?
Ну первый факт — рассмотрим два возможных отрезка (произвольных длин), кандидатов на ответ, для которых выполнено условие, они либо не пересекаются, либо один вкладывается в другой, потому что если они как-то пересекаются, то у этих отрезков концевые элементы равны — поэтому можем просто взять один отрезок большей длины, таким образом увеличив длину.
т.е. можем разбить весь массив на непересекающиеся подряд идущие отрезки. если запрос был просто на массиве — нам нужно было выбрать максимальный из этих отрезков.
посчитаем для каждого i, такой максимальный индекс f[i] (f[i] >= i), что отрезок [i..f[i]] удовлетворяет условию.
теперь, когда приходит запрос, начнем в l, перейдем в f[l] + 1, затем в в f[f[l] + 1] + 1, и т.д, т.е. будем прыгать на элемент после правой границы отрезка [i..f[i]], сохраняя максимум среди длин всех отрезков, по которым прошли. рано или поздно наступит следующее: либо мы просто придем в r (вернее, на следующий после r) — тогда все, максимум найден, либо следующий прыжок из i будет за правую границу, т.е. f[i] > r, отметим, что в этом случае a[i] будет больше либо равен всех элементов на суффиксе [i..r]. тогда начнем ту же самую процедуру с r (мы так же заранее для всех j посчитали массив g[j] — минимальный индекс, такой что [g[j]..j] удовлетворяет условию). рано или поздно, g[j] станет меньше, чем l. тогда a[j] = a[i], т.к. если бы они были неравны, то мы могли перейти из j не за l (g[j] был бы больше l), т.к. a[i] был бы больше a[j] (как мы ранее отметили). т.е. остается один отрезок, который нельзя никак уже разбить [i..j], учитываем его в нашем ответе.
ну и последний шаг — все вот эти переходы (f[i], g[j]) предподсчитаем в массив двоичных подъемов, и будем делать наши прыжки за logN.
Спасибо.
Как решается B?
Можно перебрать a b, что a^2+b^2=d. Теперь найти кол-во пар i j, что x[i]+a=x[j] и y[i]+b=y[j]. Это делается дихом.
Дихом?
Перебрать i и искать j дихом.
Поясни, что такое дих..
Сокращения от дихотомия. Просто у нас в Беларуси все так называют.
Если вопрос в самом значении слова, то дих — это дихотомия, проще говоря — бинарный поиск.
Ясно, спасибо.
Как решать задачу А?
Всегда существует оптимальное решение следующего вида — разобьем всю последовательность на отрезочки и сначала заберем все числа из первого отрезочка (внутри отрезочка берем числа в обратном порядке), потом из второго отрезочка и так далее. К примеру, если мы разбили последовательность на отрезки вот так: [a1 a2 a3][a4 a5][a6 a7 a8 a9], то забирать числа будем в порядке a3, a2, a1, a5, a4, a9, a8, a7, a6. Доказывать это сейчас не буду.
Дальше получается довольно простое ДП: f(k) - максимальная сумма, которую можно получить убрав префикс длины k. Переход будет такой:
f(k) = f(k - 1) + ak + 1, если последний отрезочек будет длины 1;
Замечаем, что второй переход можно записать вот так:
А как вы решали задачу J?. Была идея, но никак не мог реализовать.
Решение: Бинарный поиск по ответу.
Сначала очень просто можно узнать, какое максимальное число вхождений у нас может быть.
Просто возьмем и посчитаем, какое максимальное кол-во вхождений какой-нибудь буквы мы имеем. Назовем это кол-во вхождений need.
Давайте научимся проверять какую-нибудь длину len. Проверять длину len — значит узнать, есть ли у нас такая подстрока длины len, что она имеет need непересекающихся вхождений.
Это можно делать за используя полиноминальные хэши. Посчитаем хэш всех подстрок длины len. Выпишем такие пары (hash, position) — хэш подстроки и позиция подстроки. Теперь давайте для каждого уникального hash выпишем все его position в возрастающем порядке. Теперь, зная все position для фиксированного hash не составляет труда посчитать максимальную подпоследовательность из этих позиций, что разница между соседними элементами подпоследовательности больше либо равна len (это условие нужно, потому что мы ищем непересекающиеся вхождения). Это можно легко подсчитать используя ДП:
Пусть a — это подпоследовательность, в которой нужно найти максимальную подпоследовательность, чтобы соседние элементы различались не меньше чем на len. Напоминаю, что все числа в этой последовательности в возрастающем порядке.
Теперь можно просто считать следующее ДП:
fi — максимальная длина подпоследовательности из префикса a длины i. Понятно, что f0 = 0
Подсчет данного ДП ведется так:
fi = max(fj, f0) + 1, где j — такая максимальная позиция, что ai - aj ≥ len. Если такой позиции нет, то j = 0. Найти такое j можно бинарным поиском.
Как говорилось выше: давайте для каждого уникального hash выпишем все его позиции и запустим на них вышеописанное ДП. И возьмем максимум среди всех результатов запуска ДП. Это и будет максимальное кол-во непересекающихся вхождений строки, имеющей длину len. Теперь легко проверить подходит длина len или нет.
Также надо заметить, что если подходит длина len, то и длина len - 1 тоже подходит, значит можно использовать бинарный поиск, чтобы найти максимальное len, которое подходит.
Итоговая асимптотика решения: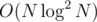
Для лучшего понимания выкладываю код.
Есть решение проще.
Сначала найдем need. Теперь фиксируем первую букву ответа (26 вариантов), и перебираем длину ответа, добавляя новый символ — суммарно будет сделано не больше n операций для каждой буквы. Итого, решение за 26n. Код.
Спасибо за такое короткое решение :) Никогда бы не додумался.
Ого,мне до этого еще учиться и учиться..
Контесты в тренировках:
К двум предыдущим интернет-олимпиадам на сайте выложены презентации с разбором от авторов. К этой подобной радости не ожидается?