For each digit x you can count the number of digits y that because of some broken sticks x is shown instead of y by hand. for example when x = 3, y can be 3, 8 and 9. Let's denote this number by ax. Then if the input is xy (the first digit shown in the counter is x and the second is y) the answer will be ax × ay.
- If a < b then there is no answer since
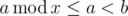 .
. - If a = b then x can be any integer larger than a. so there are infinite number of answers to the equation.
- The only remaining case is when a > b. Suppose x is an answer to our equation. Then x|a - b. Also since
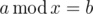 then b < x. These conditions are necessary and sufficient as well. So the answer is number of divisors of a - b which are strictly greater than b which can be solved in
then b < x. These conditions are necessary and sufficient as well. So the answer is number of divisors of a - b which are strictly greater than b which can be solved in 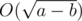 .
.
Consider a string consisting of '(' and ')' characters. Let's build the following sequence from this string:
a0 = 0
for each 1 ≤ i ≤ |s| ai = ai - 1 + 1 if si = '(' and ai = ai - 1 - 1 otherwise. (The string is considered as 1-based index).
It can be proven that a string is beautiful if the following conditions are satisfied:
for each 0 ≤ i ≤ |s| ai ≥ 0.
a|s| = 0
Using the above fact we can prove that if in a beautiful string we remove a ')' character and put it further toward the end of the string the resulting string is beautiful as well. These facts leads us to the following fact: if we can move a ')' character further toward the end of string it is better if we'd do it. This yields the following greedy solution:
We'll first put exactly one ')' character at each '#' character. Then we'll build the sequence we described above. if the first condition isn't satisfied then there is no way that leads to a beautiful string. So the answer is -1. Otherwise we must put exactly a|s| more ')' characters in the place of last '#' character. Then if this string is beautiful we'll print it otherwise the answer is -1.
We call an index i(1 ≤ i ≤ |s|) good if t equals si - |t| + 1si - |t| + 2... si. To find all good indexes let's define qi as the length of longest prefix of t which is a suffix of s1s2... si. A good index is an index with qi = |t|. Calculating qi can be done using Knuth-Morris-Pratt algorithm.
Let's define ai as the number of ways to choose some(at least one) non-overlapping substrings of the prefix of s with length i (s1s2... si) so t is a substring of each one of them and si is in one the chosen substrings(So it must actually be the last character of last chosen substring). Then the answer will be 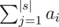 .
.
Also let's define two additional sequence q1 and q2 which will help us in calculating a.
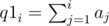
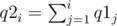
The sequence a can then be calculated in O(n) as described below:
If i is not a good index ai = ai - 1 since in each way counted in ai the substring containing si also contains si - 1 so for each of these ways removing si from the substring containing it leads to a way counted in ai - 1 and vice-versa thus these two numbers are equal. If i is a good index then ai = q2i - |t| + i - |t| + 1. To prove this let's consider a way of choosing substring counted in ai. We call such a way valid. The substring containing si can be any of the substrings sjsj + 1... si (1 ≤ j ≤ i - |t| + 1). There are i - |t| + 1 valid ways in which this substring is the only substring we've chosen. Number of valid ways in which substring containing si starts at sj equals to q1j - 1. So the total number of valid ways in which we've chosen at least two substrings are equal to 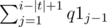 which is equal to q2j - 1. So ai = q2i - |t| + i - |t| + 1.
which is equal to q2j - 1. So ai = q2i - |t| + i - |t| + 1.
We'll first create a rooted tree from the given segments which each node represents a segment. We'll solve the problem using dynamic programming on this tree. First of all let's add a segment [1, n] with probability of being chosen by Malek equal to 0. The node representing this segment will be the root of the tree. Please note by adding this segment the rules described in the statements are still in place.
Let's sort the rest of segments according to their starting point increasing and in case of equality according to their finishing point decreasing. Then we'll put the segment we added in the beginning. A segment's father is the right-most segment which comes before that segment and contains it. Please note that since we added segment [1, n] to the beginning every segment except the added segment has a father. We build the tree by putting a segment's node child of its father's node.
In this tree for each two nodes u and v which none of them are in the subtree on another the segments representing these two nodes will not overlap. Also for each two nodes u and v which u is in subtree of v segment representing node u will be inside(not necessarily strictly) segment representing node v. We define mxi as the maximum money a person in the segment i initially has. mxi can be calculated using RMQ. Let's define ai, j as the probability of that after Malek finishes giving his money the maximum in the segment i is at most {mx}i + j. The properties of the tree we built allows us to calculate ai, j for every i and j in O(q2) (since 1 ≤ i, j ≤ q). If number of the segment we added is k then the answer will be 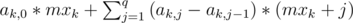 .
.
Calculating ai, j is described below:
Suppose f is a child of i and suppose Malek doesn't accept the i-th recommendation. Then since we want the maximum number after money spreading to be at most mxi + j in segment i and since f is inside i we want the maximum number after money spreading to be at most mxi - mxf + j. If Malek accepts the recommendation then we want it to be at most mxi - mxf + j - 1. So if probability of i-th recommendation being accepted by Malek be equal to pi then 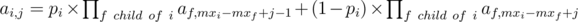 . Using this formula we can calculate ak, j recursively and calculate the answer from it in O(q2). The overall complexity will be O(nlgn + q2). nlgn for creating RMQ used for calculating the array mx and q2 for the rest of the algorithm.
. Using this formula we can calculate ak, j recursively and calculate the answer from it in O(q2). The overall complexity will be O(nlgn + q2). nlgn for creating RMQ used for calculating the array mx and q2 for the rest of the algorithm.
We solve this problem by answering queries offline. We'll first store in each vertex v number of vertices such as x for which we must calculate f(v, x) . starting from the root. We'll keep two arrays a and b. Suppose we're at vertex v right now then ai equals d(i, v)2 and bi equal d(i, v). Having these two arrays when moving from vertex v to a child with an edge with weight k one can note that bi for all is inside subtree of v decreases by k and all other bis gets increased by k. Knowing this fact one can also update array a as well. To calculate f(v, x) it's enough to be able to calculate sum of ais for all i inside subtree of x. Handling each of these operations is a well known problem and is possible using a segment tree. Overall complexity is O((n + q)lgn). There is an online solution using dynamic programming as well.
Let's first solve this problem for another game: Suppose that we've an n × n table. Each cell have some(possibly zero) marbles on it. During each move the player chooses a square with side-length at most k which its lower-right cell has at least one marble, he removes one marble from it and puts one marble in every other cell of this square. One can notice that in such game each marble is independent of the others and doesn't affect other marbles. So one can see this game as some separate games played on some tables. More formally for each marble placed in a cell such as (i, j) consider the game when played on a i × j table which the only marble placed on it is at its lower-right cell. Let's denote the Grundy number of this game by gi, j. Then according to Grundy theorem the first player has a winning strategy if and only if the xor of gi, j for every cell (i, j) having odd number of marbles on it is positive.
To calculate gi, j note that the first move in such game must be choosing a square with its lower-right cell being the lower-right cell of table. So the only thing to decide is the side-length of chosen square at the first move. Let's say we choose the first square width side length l. Grundy number of the next state will be equal to xor of gc, d for every i - l < c ≤ i, j - l < d ≤ j. Using this fact one can calculate gi, j for all (1 ≤ i, j ≤ a) (a being an arbitrary integers) in O(a3).
If we calculated the first values of gi, j one can see a pattern in the Grundy numbers. Then one can prove that gi, j = min(lowest_bit(i), lowest_bit(j), greatest_bit(k)) where lowest_bit(x) = the maximum power of 2 which is a divisor of x and greatest_bit(x) = the maximum power of 2 which is not greater than x.
Now let's prove that our first game(the game described in the statement) is actually the same as this game. Suppose that a player has a winning strategy in the first game. Consider a table containing one marble at every cell which is white in the table of the first game. We'll prove that the same player has winning strategy in this game as well. Note that a cell is white in the first game if and only if the parity of marbles in the second game is odd so there is at least one marble on it. So as long as the other player chooses a square with its lower-right cell having odd number of marbles in the second game, his move corresponds to a move in the first game so the player having winning strategy can counter his move. If the other player chooses a square with its lower-right cell having even number of marbles, it means the cell had at least 2 marbles on it so the player can counter it by choosing the same square which makes the parity of every cell to be the same after these 2 moves. And since it can be proven that both of the game will end at some point then the player has winning strategy in this game as well. The reverse of this fact can also be proven the same since if a player has a winning strategy there is also a winning strategy in which this player always chooses squares with lower-right cell having odd number of marbles(since otherwise the other player can counter it as described above) and counters the moves of the other player at which he chose a square with lower-right cell having even number of marbles by choosing the same square(since the Grundy number by countering in this way won't change the Grundy number and thus won't change the player with winning strategy).
So if we consider a table having one marble at each of the cells which are in at least one of the rectangles given in the input we only need to calculate the Grundy number of this state and check whether it's positive or not to determine the winner. To do this for each i(1 ≤ i ≤ greatest_bit(k)) lets define ai as the number of cells (x, y) which are contained in at least one of the given rectangles, 2i|x and 2i|y. Lets also define agreatest_bit(k) + 1 = 0. Then according the fact we described above about gi, j the number of 2is which are xored equals ai - ai + 1. Knowing this calculating the Grundy number of the initial state is easy. Calculating ai is identical to a very well-known problem which is given some rectangles count the number of cells in at least one of them and can be solved in O(mlgm) (m being number of rectangles). So overall complexity will be O(mlgmlgk).
If there is any problem in the editorial please feel free to note that to us.
Thank you.










For problem C: to build the "tree" one can just sort the segments according to their length, and then for each segment s we just iterate over the shorter segments s', and if s' is contained in s and doesn't have a "father", we set the father of s' to s.
We also can use set instead of rmq for finding mxs, since segments are "almost" disjoint: again we can iterate over the segments ordered by length, and since we already processed all the "children" of our segment, we just need to iterate over "alive" elements in range [ls, rs], which were not erased from the set, and "kill" (erase) them (code)
We can even get rid of logarithmic structures if we build a tree by walking from left to right with a stack of currently opened segments and assign each number to a segment on the top of the stack.
We can even do that part in O(n) by simply iterating over all 'new' elements in array :>. Though that approach may be a little bit uglier, because we need to calculate the difference of a segment and few segments inside it which needs some ifs.
Hello,all the programmers.I'm a very stupid man and now I come to ask a very stupid question. I can understand the solution,but How can you come up with such a solution? In other word,is this solution comes from a very useful model? Thanks for your answer.
Did D require heavy-light decomposition or was there a simpler solution?
I think that keeping informations like:
1) number of vertices in subtree
2) sum of distances to vertices in subtree
3) sum of squared distances to vertices in subtree
was sufficient. (Note that this isn't a coincidence that these are in fact summed d(v, x)k for k = 0, 1, 2 :P)
Maybe we should have kept that also for "upper subtrees", but I didn't think about it in details, but something like that should work and I guess that you won't find many HLD's in accepted codes.
Yeap, one can just follow the idea you described:
It's easy to see how to compute these values if we've already done that for each of the children. The main observation is that
So, one dfs is enough to compute all three values. Then using second dfs one can compute the same values for "upper-tree" (the complement of the S(v)) — number of verticies outside the subtree, sum of the distances from vertex v to all the verticies outside the subtree and sum of their squares.
Then, if one already knows all the values described above and the distance between verticies u and v, one can easily answer the query: it's a combination of pre-computed values. For me it was easier to distinguish special case when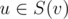 .
.
Unfortunately, to compute the distance between verticies u and v we need to know their lca, but that's just one more for-loop (using "binary-jumps" technique).
Ah, upper trees would make sense I guess. I ended up calculating the same sum for all light edges and stored partial sums for all paths but I guess that was overkill. And then I forgot modulo in one place and couldn't find it in time :D
For Treasure problem can anyone tell a test case for my solution?
thanks in advance
((((()#)
Here you go.
In the text about B, what means "Then x|a - b" ?
That mean x is a factor of (a-b), or x is divisor of (a-b)
Read it as x is a divisor of a − b or x divides a − b, which means a − b would leave no remainder if divided by x.
http://codeforces.com/contest/495/submission/9124214 This is my understanding B editorial. Where i am wrong?
You have to start the loop from sqrt(a-b) and go to b+1. In this process, you can find the other factor by (a-b)/x.
can you explain more particularly please?...
Your solution timed out because it's
O(a-b).Since our aim is to find
divisors of (a-b) greater than b, we need to loop from1 to sqrt(a-b)only.That'sO(sqrt(a-b))Here's my solution.9119032
Can anyone write explanation how results in 3rd test case of Helping people are obtained?
Actually, you can just write a program that will run through all possible accepted recommendations subsets and calculate the expectation easily and you'll see it's a right answer.
Somehow, I get 4.45 instead of right answer.
I bet you are computing maximum of expectation, not the expectation of maximum.
Would you mind showing your bruteforce program?
As I see from your submission, that was the case. You only add probability on segment, but that is not right: this way, you only get 4.45 as maximal possible value, while the real maximum can be 6, achieved at point 2 when 1, 2, 3 and 5 segments are "accepted".
Here's mine: 9129004
I have the same question about how the expected maximum is calculated. Would anyone care to kindly explain the third sample ?
Here is my comment in Russian http://codeforces.com/blog/entry/15134#comment-200974
Let's count the probability that maximum equals to some value. It certainly can't be less than 3.
Maximum equals 3 in the only case when the first recommendation is rejected (0.5) and among recommendations 2, 3, 5 there are at least two rejected: this probability equals to 0.25(1 - 0.8)(1 - 0.9) + (1 - 0.25)0.8(1 - 0.9) + (1 - 0.25)(1 - 0.8)0.9 + (1 - 0.25)(1 - 0.8)(1 - 0.9) = 0.215, so with probability 0.5·0.215 = 0.1075 maximum value equals to 3.
Maximum equals 5 in the only case when exactly 3 among the recommendations 1, 2, 3 and 5 are accepted, this happens with the probability (1 - 0.5)·0.25·0.8·0.9 + 0.5·(1 - 0.25)·0.8·0.9 + 0.5·0.25·(1 - 0.8)·0.9 + 0.5·0.25·0.8·(1 - 0.9) = 0.3925.
Maximum equals 6 in the only case when all the recommendations 1, 2, 3, 5 are not rejected, this probability equals to 0.5 × 0.25 × 0.8 × 0.9 = 0.09.
In all the other cases maximum value equals 4: this probability is 1 - 0.1075 - 0.3925 - 0.09 = 0.41.
And let's finally count the desired expectation: 3·0.1075 + 4·0.41 + 5·0.3925 + 6·0.09 = 4.465.
Thank you sir.
Coding of problem E was made to be as tedious as it can be... Why those coordinates were so big? That required some scaling them, but keepeing their original coordinates or a dynamic interval tree (I chose dynamic tree), but that was not that easy to squeeze it in TL, even though there were at most 50000 rectangles and TL was 5s. After some attempts I managed to fit within 4.8s :P.
Coming up with solution was pretty funny. If somebody started to thinking about those nimbers, he was screwed :P. I wrote a program to calculate them for me for some small values of coordinates and k and it took me 5 minutes and it was crystal clear what they are :P. I was lucky that I didn't do this during contest, because I would fail at coding it :P.
Sorry for off-topic question, but why do you have bunch of
using std::in your code? Why not justusing namespace std?Because I'm angry when I use variable names such as "left", "end" or "hash" and compiler is mad at me, because those names are in std and I can't use them. Though I once suffered from doing so, because I haven't got "using std::abs;" in my code and there exists abs function not in std, but it casted long longs to ints and I needed a lot of time to find this xd.
Ah, I see. Though I think this is better solution:
Hm, nice idea, maybe I should consider changing that :).
Little unrelated, does anyone know how to avoid 100000 errors when you accidentally try to do find the
maxof int and longlong?When you don't need
double, this is useful :#define max max<long long>Or
How about a macro?
Try to using with max segment tree. O(N) for each query.
If
aandbare functions, one of them will be called twice if you use that macro.Yes. I have faced that problem before. I usually save the return result of a function in a variable, and than use the macro. It is kind of inefficient, and I have to stay aware of it all the time. Do you know any easy workaround for it?
My solution for problem div1-d contains setswap lol
For Div1 B, can someone explain a solution with KMP and DP? (and/or a implementation)
A detailed solution was given above in the editorial.. why don't you read that?
fuk you
using kmp we can find out what are the indices j at which a pattern
S[i],S[i+1],...S[j] equals string T. let us call these indices as good indices.
create a string G = T+ "#" + S and compute prefix table for G now whichever indices of prefix table from index T.length+1 to G.length()-1 inclusive (ZERO BASED INDEXING), equals T.length is a good index. why? (because at this index prefix of string G with length T.length(which is T itself) equals the suffix G[curIndex-T.length+1]..G[curIndex]) means it is a good index .
now consider following three arrays dp[S.length], q1[S.length], q2[S.length]
dp[i] denotes the number of partitions whose last partition ends at index i
q1[i] denotes total number of valid partitions possible in prefix with first i+1 characters or (prefix upto index i)
q2[i] denotes sum of q1[0],q1[1], .., q1[i]
Calculation for dp[i],q1[i],q2[i]
if i is not a good index then dp[i] = dp[i-1] , because exactly dp[i-1] new partitions will be added. valid Partitions which were ending at index i-1 can end at index i safely because it is not possible for a new occurence of string T(as index i is not a good index)
suppose you are given an array a[n] and Q queries in each query you are given an index i(ONE BASED) and you have to tell the value of i*a[1]+(i-1)*a[2]+ ... + a[i-1] the problem can be solved using prefix sum of prefix sums, means first calculate prefix sum array p1 and than calculate prefix sum of array p1 into array p2 now the result of query for index i will be the value of p2[i]
the dp[i] for good indices consists of two parts 1. without using any previous partition 2. with using some previous partitions for first part their will be exactly i-T.length+2 partitions which are k=1(single substring selected as a single partition) substrings starting from index 0,1,2, .. i-T.length+1 and ending at index i.
second part -- > for each index j < i-T.length+1 considering partitions ending at index j(dp[j]) we can append a new partition starting from index j+1,j+2 .. ,i-T.length+1 and ending at index i. this equals to adding dp[j] exactly i — j — T.length + 1 times to dp[i]. as discussed in previous spoiler we can use prefix sum of prefix sum to calculate second part of dp[i]
Hope it's clear but please correct me if I am wrong somewhere , I have written this comment just to check my understandin of editorial.
thank you!
can you please review my profile what can I do to improve , I am doing practice but I get stuck in almost all contests .
solve slightly difficult problems (1600 — 1900). I think it will help you.
To make E a bit simpler, we don't need to count exact value of our game, we just need to if whether it's zero or nonzero, so it turns out that we don't need any computing of ai - ai + 1, because if our state equals zero then all ai's are even!
By the way, I was waiting for editorial for E, because I wanted to know why those nimber values behaves that way and it was the only place which was described by magical phrase "Then one can prove" :P. Though I didn't try hard to do that by myself, is it easy?
Can someone help me to explain the first simple test in Problem B div.1? I have read the statement many times but still can not understand :(
012,0123,01234,234,1234. Where a digit represents an index.
Can you please explain the third test case as well ? I can't figure it out. Thanks.
There are 12 partitions for ddd:
[0], [1], [2], [01], [12], [012], [0][1], [0][2], [1][2], [0][12], [01][2], [0][1][2]
Yes, of course.
k = 1 : {1}, {2}, {3}, {12}, {23}, {123}
k = 2 : {1, 2}, {1, 3}, {2, 3}, {12, 3}, {1, 23}
k = 3 : {1, 2, 3}
What is the mysterious statement "Then one can prove that" in problem E editorial? I just can't get the proof. Many game problems are like that: some patterns not hard to be found yet when I want a mathematically correct answer(proof) rather than a simple AC code, then no one will help me.
9112598
?! Compare?.. Are you serious?
Wow. There's a rather nasty ambiguity in the definition of problem E, Sharti.
Nowhere does it say what happens when the L by L square that you are complementing must be 100% inside the original board. I just assumed that if it went off the board that was fine -- it just complemented the ones in the square that were on the board. It turns out that this is NOT the definition that was intended. In their definition the full L by L square must fit entirely within the original board. This changes the game.
In my interpretation the "simple pattern" of the nimbers (grundy numbers) does not hold. Without that pattern the problem is impossible to solve.
I have an objection about the 495C - Treasure (Div.1 link is 494A - Treasure.)
I think problem description is wrong (i.e. it does not correspond to the tests and to the tutorial).
According to the problem description, string
(()))(should be considered beautiful given that |s|=4.Thus, for s=
((#(input string output must be 3, not -1 (test 19 in 9266684).I appeal to the following note in problem description: "|s| denotes the length of the string s." "Length of the string s", not "the length of a string which we got after replacing
#characters with)characters".What do you think?
I don't think the description is misleading.
From question itself "After spending a long time Malek managed to decode the manual and found out that the goal is to replace each '#' with one or more ')' characters so that the
final string becomes beautiful."So he have to make final string beautiful and not any string. Then he poses the conditions for any string to be beautiful.
This implies string
(()))(isn't beautiful and hence #19 must output -1.For 494C — Helping People, the time complexity is said to be O(nlgn + q^2), nlgn for RMQ and q^2 for dp. But what about the time used to construct the tree? My understanding is that if every tree is disjoint, then the tree would take O(n^2) time to build, because every segment simply need to traverse all previous segments until the sentinel segment node. Am I right?
-I haven't solved it yet-
See that we must sort the interval first, so I don't think we need to traverse all previous segments
First, sort the interval (like in the editorial: "Let's sort the rest of segments according to their starting point increasing and in case of equality according to their finishing point decreasing.") – O(N)
After that, assign
Node v = root(node with interval [1, n]), we iterate through the sorted interval:if current interval is in current node's interval (v.left <= interval[i].left && interval[i].right <= v.right): we add a child u to v with interval [interval[i].left, interval[i].right], then move to node u (
v = u)else: we move to the parent of current node (parent of v) (
v = v.parent), repeat (1)The construction of the tree will be about O(N).
Overall: O(NlgN) + O(N) = O(NlgN)
Hope it helps!
Problem B Div1: Can anyone Please Explain the third sample case:
[0-0],[1-1],[2-2],[0-1],[0-2],[1-2],[0-0,1-1], [0-1,2-2],[0-0,1-2],[0-0,2-2],[1-1,2-2],[0-0,1-1,2-2]