Panoramix's Prediction (problem A, div-2). The problem's author is Alex_KPR | ||
| In the very beginning of statement you may find some words about what is prime number and what is next prime number. Main point of problem is to check is m next prime after n or not. Problem statement guarantees that n is prime number. We need to check only two cases: 1. Number m is prime, and 2. There is no any prime number between n and m Really, if there is prime number k between n and m then m cannot be next prime after n. Restrictions in this problem are really small and there is a way to solve it: for(int i=n+1;i<=m;i++) where prime(i) is any correct way to check is number i is prime. Another simple solution of this problem is to conside the fact that restrictions are no more than 50. It is possible to find all pairs n and m by hands and write solution formed by series of cases like this: if (n==2 && m==3) return "YES"; This solution gets "accepted" too. | |
| Complexity may be various because of diffenent realizations and is in range from O(1) to O(n + m). If you are interested in why your solution gets "wrong answer" the test "2 5" maybe helps you. |
| Depression (problem B, div-2). The problem's author is Marishka | |
| The first I pay your attention is while we are moving first arrow the second one is stay motionless. In fact this means that we can solve next two problems independently: 1. Find the angle to turn the minute hand, and 2. Find the angle to turn the hours hand Next, you may find in statement phrase: "Cogsworth's hour and minute mustache hands move evenly and continuously". It means that after every little increasing of time Δt both hands will move for some little angles. Number of minutes is always integer because of format HH:MM so every new minute will add 360 / 60 = 6 angles to minute hand. For angle of hours hand influence number of hours and number of minutes. Every new hour will add 360 / 12 = 30 angles to rotate and every new minute will add (360 / 12) / 60 = 0.5 angles. Thus, we should cut number of hours and number of minutes from HH:MM entry and use formulaes described above for finding the answer. Look at the time before midday and after noon carefully, analog watch has no difference between them and answers for 08:15 and 20:15 should be equal. | |
| Complexity is O(1). If you are interested in why your solution gets "wrong answer" the tests "20:15" and "00:00" maybe helps you. |
| Heroes (problem C, div-2 and problem A, div-1). The problem's author is Alex_KPR | |
| It is possble to solve this problem by full search because there are only k = 7 heroes and three team. Let's find all dividings - move every hero in every team and drop away incorrect dividings when al least one team is empty. In each correct dividing we should find value of experience between two heroes who will receive the maximum and minimum number of experience points and value of total amount of liking in teams. Now we should choose the best way and write it. | |
Complexity is O(3k· k2). |
| Falling Anvils (problem D, div-2 and problem B, div-1). The problem's author is dagon | |
| In this problem you were to determine the probability if the equation It's equivalent to the condition of non-negativity of the discriminant D = p - 4q. To solve this problem you might draw a rectangle on the (p,q)-plane with the vertices in points (0, - b), (a, - b), (a, b) и (0, b) and line p = 4q. Every point of the rectangle corresponds to possible value of p and q and the line divides the plane into two parts where the equation has real solutions and where it hasn't. Then because of equiprobability and independence of choosing p and q the answer is the area of the intersection of the rectangle and p ≥ 4q set divided by the area of the rectangle in case of it's nonsingularity (a, b ≠ 0). If single number among a and b is equal to zero, the rectangle degenerates to the segment and the sough-for probability is equal to ratio of length of intersection of the segment and p ≥ 4q set and the lenght of the whole segment. In case a = b = 0 the answer is evident and equal to 1. |
|
Complexity is O(t). If you are interested in why your solution gets "wrong answer" the mini-tests "0 1", "1 0" and "0 0" maybe helps you. |
| Beavermuncher-0xFF (problem E, div-2 and problem C, div-1). The problem's author is Marishka | |
| Let's assume that in vertix v it is possible to find pair of values < xi, yi > for every child vi where xi is maximal amount of beavers which can eat beavermuncher if it comes to vertix vi and return back, and yi is amount of beavers which will still alive in vertix vi after beavermuncher's ride. Let's sort all children vi by value of xi. We should visit vi in sorted order from highest value of xi to lowest while there is possible to return back to root. If after ride to all children vertix v contains of some non-eaten beavers we must continue eating by following way. Let's find some value of yj which is greater than zero. We should move to vertix vj and after that move back to v. This operation must be executed as many times as possible. Of course, the process shouldn't be emulated, we may repeat this way with vertix vj for min(b, yj) times, where b is amount of beavers in vertix v which are remaining. So we find a pair < x, y > for vertix v by knowing values < xi, yi > for every child vi, where x is amount of eaten beavers and y is b - number of remaining beavers. Answer is a value of x for staring vertix s. |
|
Complexity is O(n· logn). If you are interested in why your solution gets "wrong answer" the tests with n = 1 maybe helps you. |
| Domino Carpet (problem D, div-1). The problem's author is Alex_KPR | |
| Look at squares of Domino Carpet. They are can be only in one of this three states: 1. Here can be any domino chip 2. Here can be only horizontal domino chip 3. Here can be only vertical domino chip No matter what is in squares, only their states are important. Look at the any pair of columns j and j + 1 where in some row located horizontally chip of domino. We may cut this pair of jointed columns n × 2 from carpet and don't be afraid about cutting some another chips. So, this pair of columns may be completed independently from another columns. If n is even number it is possible to complete some columns of single width, not only pair of columns. There is only way to do this - we should put all dominoes vertically. This formula is describing all situations above: dj = (dj - 2· qj - 2) + (dj - 1· pj - 1), where j is an amount of completed columns, pj is an amount of all possible ways to complete only j-th column (it can be only 0 or 1) and qj is an amount of all possible ways to complete j-th and j + 1-th columns. Obviously, this formula is incorrect. If some pair of jointed columns we will complete by only vertical dominoes then this way will be counted twice. Let's use the fact that it is unique situation when this formula is incorrect and improve it: So, dj = (dj - 2· qj - 2) + (dj - 1· pj - 1) - (dj - 2· pj - 2· pj - 1). In dm is answer to the problem. The only trouble is we need to count pj and qj. pj is 1 when n is even and in j-th column there are no squares in state "here can be only horizontal domino chip". Otherwise pj is 0. qj can be found by dynamic programming. For every row we should try to put one horizontally oriented domino chip or two vertically oriented and use information about states in observable squares of carpet. | |
Complexity is O(n· m). |
| Martian Food (problem E, div-1). The problem's author is dagon | |||||
| The problem can be solved using the inversion conversion. Inversion is the conversion transfering a point with the polar coordinates (r, φ) to a point Assume the plate a circle with center in (R, 0) and radius R and Honduras - circle with center in (r, 0) ans radius r. Then Guadeloupe and Bull Terriers are situated as on the first picture.
After applying the inversion conversion the border of the plate transfers to the line |
| ||||
Complexity is O(t). |



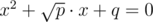 has at least one real root, assuming that values
has at least one real root, assuming that values 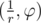 . It's stated that the inversion transfers straight lines or circles to straight lines or circles. Straight line can be image only of line or circle that includes home (center of the inversion).
. It's stated that the inversion transfers straight lines or circles to straight lines or circles. Straight line can be image only of line or circle that includes home (center of the inversion).

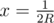 and the border of the honduras - to the line
and the border of the honduras - to the line 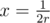 , Guadeloupe and Bull Terriers becomes circles between them, see the second picture. It's easy to find the
, Guadeloupe and Bull Terriers becomes circles between them, see the second picture. It's easy to find the 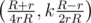 . To find the radius of the bull terier draw a line through the home and the center of the image of the need honduras. It's possible to prove that the prototypes of this points are diametral points on the bull terrier. So the answer is the distance between them divided by two.
. To find the radius of the bull terier draw a line through the home and the center of the image of the need honduras. It's possible to prove that the prototypes of this points are diametral points on the bull terrier. So the answer is the distance between them divided by two.







To problem E — Martian Food, I suggest to watch the video "Epic Circles" of Numberphile in youtube in order to get a better explanation and concepts about inverse circles
242986607 I solved the A problem like that. I hope it might help someone one day.