Всем доброго времени суток!
Недавно я заинтересовался следующей проблемой: пусть у нас есть плоскость, на которой проведено n прямых общего положения — то есть, никакие 2 не параллельны, никакие 3 не пересекаются в одной точке. Ясно, что эти прямые разбивают плоскость на некоторые части — притом, площадь некоторых конечна, а некоторых — бесконечна. Подсчитаем число частей, которые являются треугольниками. Поставим теперь "экстремальную" задачу — обозначим за f(n) минимальное число треугольников, которое может получиться, а за g(n) — максимальное.
Оказывается, что f(n) = n - 2 для любого n ≥ 3. Эта теорема была недоказанной на протяжении больше сотни лет, пока ее не доказали достаточно хитроумным способом, описанным, например, в статье "Треугольники и катастрофы".
К сожалению, найти какие-то оценки на величину g(n) в Интернете у меня не получилось. Можно, однако, получить тривиальную квадратичную оценку с помощью формулы Эйлера: рассмотрим нашу картинку как планарный граф — вершинами будут точки пересечения прямых, ребрами — те отрезки между вершинами, которые более ничем не пересекаются. Обозначим количество вершин за V, ребер — за E, граней (частей с конечной площадью) за F. На приведенном рисунке V = 10, E = 15, F = 6. Вообще, нетрудно перебрать все варианты и обнаружить, что g(5) = 5.
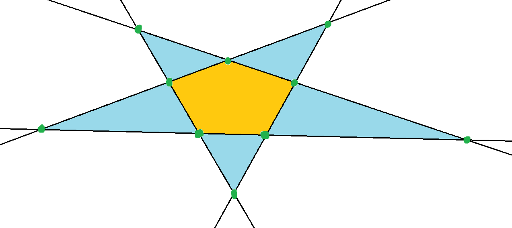
Как известно из формулы Эйлера, V - E + F = 1(мы не учитываем "внешнюю" грань). V и E по несложным соображениям можно высчитать как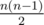 
и n(n - 2), отсюда мы видим, что количество частей с конечной площадью независимо от разбиения равняется 
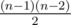— собственно, это и дает тривиальнейшую оценку на количество треугольников как что-то порядка 
.
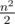В связи с этим возник вопрос — а достигается вообще ли эта оценка? Чтобы показать определенную нетривиальность задачи подмечу, что g(9) ≥ 14:
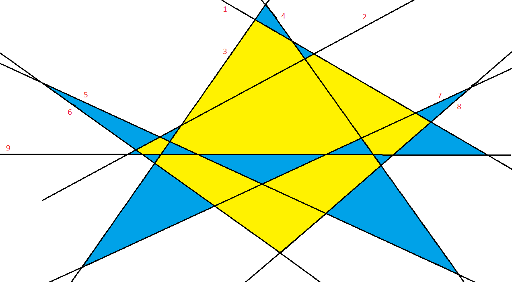
Update челлендж закрыт, поскольку я ошибочно предполагал, что g(n) имеет порядок не больший, чем nlog(n) и господа Endagorion и Ripatti привели квадратичные примеры. Собственно, с задачей я встретился, пытаясь улучшить константу вот здесь — если есть любители математики, которые захотят порешать:)
Возьмем n + 1 почти вертикальных и n + 1 почти горизонтальных прямых, они образуют разбиение на n2 клеточек (и какие-то другие области, на которые пофиг). Проведем 2n - 1 прямых, примерно параллельных диагоналям сетки так, чтобы в каждой клеточке был треугольник. Получилось Ω(n2). Где я неправ?
Кажется, вы правы, я даже и не предполагал, что есть квадратичный пример:) Притом, если я правильно нарисовал, получается, что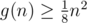
. Интересно — а 
можно улучшить?
Вообще, на самом деле это логично, иначе подсчет матожидания вот в этой задаче давал бы гораздо лучшую асимптотику, чем
, что сомнительно:)
Ну, одна восьмая — это конструкция, которая сходу в голову пришла. Разумеется, можно и лучше.
Стало интересно, как выглядят хорошие решения, поэтому быстренько набросал отжиг. Для решений, к которым он сходится,
, поэтому это выглядит правдоподобной гипотезой.
Для n = 9 лучшее решение, которое у меня есть (и оно, скорее всего, наилучшее глобально), это 21:
Еще значения: g(12) ≥ 37:
g(16) ≥ 67 (не все треугольники попали на картинку):
g(20) ≥ 105, g(25) ≥ 153. Дальше пока что отжиг плохо справляется.
Красивые рисунки, только на последнем есть зеленый четырехугольник — так и задумано?:) Вообще, примеры похожи на "звездочку" размера n — то есть, выбирается некие n точек на выпуклой фигуре типа элиппса и после этого 1-я точка соединяется с n / 2-ой, n / 2-я с 2-ой точкой, та с (n / 2 - 1)-ой, и так далее — правда, аналилизировать то, что получается внутри, не очень понятно как.
А как выглядит отжиг для этой задачи? У меня была идея задать задачу формально как функцию (x1, x2, ..., xn, α1, α2, ..., αn), где x1, ..., xn — точки, в которых прямые пересекают какую-то стороннюю прямую (к примеру, прямую y = 0), притом прямая li пересекает ее в точке xi под углом αi. Собственно, "энергия" — это (минус) количество треугольников. А как вы его реализовали?
Зеленый четырехугольник — баг, конечно.
Отжиг простой: генерим набор случайных прямых и начинаем их случайно заменять по одной (или больше, в зависимости от метода).
This thread is very far from being closed.
Proof that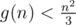
is in fact pretty easy and you can find it here: http://artofproblemsolving.com/community/c6h597095p3557339
I remember that I had once read article about it in Wikipedia and that it's still an open question to determine exact values of g, but it is possible to give very good estimations. I can't recall exact estimations, but it is possible that differences between some of them were 1. And given bound can't be much better, example with large g(n) can be improved much further than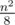
It seems funny, cause I met this problem when I was trying to improve constant c in this problem :)
Some construction like this
gives (n + 1)2 - 3 triangles for 3n lines where n ≥ 2.
Oops, my fault, it gives only
constant instead of 
I thought earlier...
It seems from Swistakk's comment that bound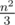
cannot be reached, but your example is nice anyway:)
By the way, aren't you an author of "Fragmentation algorithm and van der Waerden numbers" on Habrahabr?
I thought I found a counterexample for his proposition. I should check my results more diligently.
Yes, that's me.
I like this algorithm and I even added your article to bibliography in my course work in MIPT. It was concerned with question "what is the minimal N such that if we color numbers 1, 2, ..., N in C colors then exist a nontrivial monochromatic solution of equation x + y + z = 3w", and I used that algorithm to find an answer for 4 colors:)
Glad to see that my article is really useful!
UPD. Seems that this construction won't work.
Nevertheless looks like I know how to improve it a bit.
Consider 3 groups of almost parallel lines on the picture above. We can construct similar structure using them, but it will be very stretched on the plane. Like this:
We will have 3 additional constructions with n / 9 lines. After that we can split (9 groups of lines now) again and build 9 additional structures having n / 27 lines.
So, for n → ∞ we will have (n / 3)2 + 3(n / 9)2 + 9(n / 27)2 + ... + O(n) =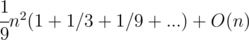
= 
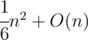triangles.
UPD. Seems that this is wrong too.
Applying the same idea to Endagorion's example, we have
Wolfram Alpha says that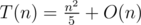
.
Hey folks, can you check this construction?
Blue lines are bundles of k almost paraller lines, red ones are bundles of 2k ones.
Black dots are Endagorion's constructions, green is mine.
We have n = 12k lines total, for any black dot we have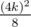
triangles and 
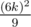for the green dot. So, total number of triangles is
Here is described a construction with n2 / 3 + O(n) triangles.
Construction is a bit similar to set of Simson lines. Cool.
Seems that lines not in general position are allowed there.
For tniangles they are in the general position (aka simple arrangement as is stated in the paper).