This was my first SRM, and I would like to thank rng_58 (algorithm coordinator + tester), KADR (tester), misof (language reviewer) and dreamoon_love_AA (author of Div1 medium) for their invaluable help.
I will try to keep this short, since the TC editorial writers are much better at writing explanations.
Div2 Easy -- FilipTheFrog
The simplest solution is to perform N iterations. Each iteration, look for a pair (i, j) such that island i is reachable and |positions[i] - positions[j]| ≤ L. Mark island j as visited. The complexity is O(N3). It works because each iteration increases the answer by at least 1 assuming it hasn't already been found, so after N iterations your answer is guaranteed to be correct.
Div2 Medium -- PublicTransit
You can fix each possibility for the teleporter and then test every pair of cells to find the longest distance. You can calculate it as follows: if the teleporter cells are at a and b, then the distance between cells x and y is the minimum of the following:
- dist(x, y)
- dist(x, a) + dist(b, y)
- dist(x, b) + dist(a, y)
The complexity is O(R4C4). I think you can improve it to O(R3C3) by observing that if one booth is at (r, c), the other booth should be at (R - r + 1, c) or (r, C - c + 1). I'm not actually sure if that's true, though. Maybe it's wrong. Can anyone prove/disprove it?
Div2 Hard -- ApplesAndOrangesHard
First, read the editorial for the easy version below.
We will use the same greedy algorithm, but we can't process every fruit directly. Let's think about the optimal answer if  weren't included. We could have floor(K / 2) apples, then ceil(K / 2) oranges, repeated until we have N fruits.
weren't included. We could have floor(K / 2) apples, then ceil(K / 2) oranges, repeated until we have N fruits.
When we are forced to add an apple, we should disrupt this pattern as little as possible. Let's sort  and keep a 'window' of size K. Initially, the window's first K / 2 elements are apples and the rest are oranges, and it represents the range of fruits [1, K]. When you move to the next element of
and keep a 'window' of size K. Initially, the window's first K / 2 elements are apples and the rest are oranges, and it represents the range of fruits [1, K]. When you move to the next element of  , cycle the window forward so that fruit number
, cycle the window forward so that fruit number  is at the end of the window. Then, pick the the apple with the greatest index, and move it to the end of the array. You have to ensure you don't pick an apple that is immovable because of a previous value in
is at the end of the window. Then, pick the the apple with the greatest index, and move it to the end of the array. You have to ensure you don't pick an apple that is immovable because of a previous value in  . The complexity is
. The complexity is 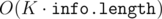 .
.
You can also solve it when K ≤ 109, but it's more trouble than it's worth.
Div1 Easy -- ApplesAndOrangesEasy
The algorithm is greedy: for each i from 1 to N, try to make the i-th fruit an apple. If it contradicts the information you have, make it an orange instead. It works because making a fruit an apple affects the next K - 1 choices, so you want to make the earliest possible fruit an apple -- that way, it becomes unimportant sooner.
Naive complexity is O(NK2); you can improve it to O(NK) by using a queue or prefix sum array or clever loop.
Div1 Medium -- CampLunch
(Problem and editorial by dreamoon_love_AA.)
If all permutation in each element of a are same, this problem just a normal Tiling problem such as UVa11270. (Before solve this SRM med problem, you may need to know how to solve UVa11270 with O(n2 * 2n) firstly.)
The main difference of this problem with UVa11270 is a student can seat in different place in consecutive two days. It cause we cannot only reserve dp status for next M seats from current seat (this kind of problem method have the status dp[row][column][the occuppied status of next M grids]). Then, how can we resolve this situation?
Here provides two method to resolve it by change dp status:
(1) Change dp status to dp[row][i-th student][the status of having plan or not of next M (day, student)].
You can imagine it as all student seat in alphabetical order, and plan 2 of lunch represent some pair of student can get double lunch in some day. By this way, you only reserved status of at most M student in dp proccess.
(2) Change dp status to dp[row][column][the status of having plan or not of next M (day,student)].
In detail, the next M (day,student) means students that have larger column number of this row in the same day and other students in next day. I think it's more difficult to imagine than previous method.
Ironically, the two methods are not provided by myself, these solution are provided by two tester. I solve it in O(2n * n3) originally. The story tell us: if you can find a good status of dp, it make your dp life better.
Div1 Hard
Fix the first teleporter at A. Now do a DFS from A. Suppose we're currently visiting B. Each node N on the path from A to B has a precomputed 'hanging value', the length of the longest path starting from N which doesn't get closer to A or B. Number the nodes on the path from 0 (A) to S - 1 (B), where the path has S nodes. When moving between nodes at positions p1 and p2 on the path (p2 > p1), we can take a direct route (length p2 - p1) or an indirect route (length (S - 1) - p2 + p1). Note that the length of the direct route is fixed, while the indirect route gets 1 minute longer with each step of DFS.
In the DFS transition, we add a node to the path. We will process this node to obtain an integer LIM, meaning that the new node enforces the constraint that we can't continue the DFS in a direction away from A and B for more than LIM steps.
How do we process the node? Suppose the node has hanging value v2 and position p2. We want to select a node on the path with value v1 and position p1 such that:
- The direct path is infeasible: p2 - p1 + v1 + v2 > X. Rearranging, we want v1 - p1 > X - p2 - v2.
- The limiting factor (LIM = X - ((S - 1) - p2 + p1 + v1 + v2)) is minimal. Rearranging, we want to maximize v1 + p1.
By converting candidate nodes (v1, p1) to diagonal coordinates (v1 - p1, v1 + p1), it reduces to dynamic RMQ and we can solve it with a persistent segment tree. The complexity is 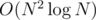 .
.











It is nice to see fast editorials of topcoder on codeforces. Thanks!
In Div1-Medium, I submitted an O(n * 3m) solution, and the last example needs 1.8~1.9 second. I assume the time it uses doesn't depend on input, but somehow it failed...
It can pass after add this line:
if(dp[i][mask] == 0) continue;My code: http://ideone.com/3Cn6Y6
Do you know why your 250 failed? I've been curious since systest ended...
Once again, I've made a mistake that examples can't save me...
My experience is that TC samples catch a little bit of the most trivial mistakes (I had a solution which assumed the input contained
As instead ofYs and passed all samples) and are useful for understanding the problem, but you can't rely on them at all to tell you if your solution's probably correct.range based for loop could have saved you
In my room there was a solution with such complexity and it has passed.
I have a simple O(N3M) solution for div1 Med. It runs in time (the time really just depends on N and M, the maxtest gives 1.2-1.8 seconds runtime), it works on the first 5 samples... but it gives WA on the last (maxtest) one.
Weird.
Actually it depends on input (not only N and M) a bit (and that cause my solution timed out).. I guess it is affected by cache miss.
Your solution seems to need more time than mine on the last sample, so mine might pass. Still, I don't get why it gives WA.
Simpler explanation to div1 500 — solve it as normal tiling problem, but doing reshuffle of students when we enter next row. So while you are processing i-th student at j-th day, you know state of first i-1 students at next day (do they have meals) and state of remaining students on this day. When new day starts, all students simply move from their old places to new ones, so you have to make a corresponding shuffle of DP results:
I implemented the same logic (DIV 2 Medium problem). I cant figure out where i am going wrong. Can u please help? Here is my code http://codepad.org/9t0HGCgj
This piece of code, lines 19-20:
misses some point pairs. It should be
tnx a lot :) got it.
You're welcome!
In editorial of Div2 Hard. I think the second 'apples' should be 'oranges'...:P in this sentence: "We could have floor(K / 2) apples, then ceil(K / 2) apples"
Thanks
in the div2 medium problem i have seen many people using the o(1) algorithm, but i don't know why, can anyone tell me, thank you very much
The solution was: min(r, c) — 1 + (max(r, c) — 1)/2. I can't prove formally its correctness, but it's somewhat intuitive.
PS: I just commented to see someone prove it for us (without having to find out the formula)!
I did this solution and was surprised it passed all tests because I didn't check its correctness. It seems (and this is what I wasn't sure of) that the best place for teleporters is always opposite corners. In this case the longest path will be between the two points 1/4 the big dimension away on opposite sides of each teleporter (any further from the teleporters and it would be shorter not to use them). You still have to travel all the smaller dimension and then 1/4 of each side on the longer dimension.
The link to UVA 11270 is broken. You seem to be missing a colon between http and //.
UPD: Fixed
Can someone explain how the normal tiling problem can be solved in O(n2 * 2n)? Where does the n2 come from?
dp state would be dp[x][y][bitmask] where (x,y) is the current cell in 2D grid which you need to process and bitmask is a n bit number showing which cells in the row are free and which are occupied. Hence there are O(n * n * 2^n) states with state transition in O(1) implying total complexity = O(n * n * 2^n)
Could you explain more detail? Why each cell has 2^n states? Bitmask is n bit number showing which cells in the row are free and which are occupied, why we don't consider each row has 2^n states?
Look at the picture below: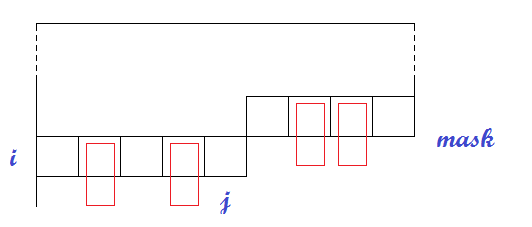
Thanks guys!
Thanks for the tutorial
Do you know that: number of perfect matchings in planar graphs can be counted in polynomial time?
Why do I put this here? Because counting numbers of filling chessboard with dominos is counting matchings in a planar graph and that was a special case of Div1 Med :P
I think you are talking about this.
Firstly thanks for sharing it, very interesting stuff.
In this particular problem, if I am not mistaken, we need to count number of matchings not just number of perfect matchings. Also, what about the shuffle at each row, how can we deal with it?
Uh, sorry, indeed, in this problem there were also 1x1 plans, I forget about them and that makes a big difference, thanks for pointing that out. And actually I don't know if we can deal with shuffling rows :P. Summing up, there are 2 big obstacles to apply mentioned algorithm to this problem (and I was aware of one of them), that was rather loosely connected fact than alternative way to solution :P.
Hard problem can be solved without pesistant segment tree in O(n^2) time. My solution