Google Code Jam online round 2 will start soon.
The top 1000 contestants will receive a limited edition of the Google Code Jam 2015 t-shirt. The top 500 contestants will advance to Round 3 to compete for finalist spots and a free trip to Google Seattle. They will also get a chance to compete in the brand new Distributed Code Jam competition.
Good luck all!
UPD: Contest starts in less than 2 hours, you can load the dashboard now.











Contest is over, let's use this thread to discuss the problem set.
How to do Kiddie Pool?
I converted in into a binary search + convex hull question and it was working on all sample cases but one. Was it a precision issue on my side or is the intended approach different?
I used Minkowski sum + linear (O(n)) search. And BigIntegers to not care about precision.
I have only vaguely heard of Minkowski sums in the context of adding convex sets which is kinda what I was trying to do. I was representing each tap as a point on a plane with coordinates as (heat rate,volume rate).
Then I binary searched on final time. For each time I did this: Let set be (0,0). Now for each point in the set add point+(time*tap1) also to the set. Retain only the hull of this set and move on to next tap. If finally my required co-ordinate lies inside this hull I shift hi to mid else lo to mid.
All I want to know is if this is even correct.
NOTE: By heat I mean temperature*volume
If you sort the points by angle (i.e. temperature), then the partial sums of this array, together with partial sums of the reversed array, will be the vertices of the convex hull. Then, you need to find the longest vector going in the direction of (V, V*X) which lies inside the hull.
Damn, I never thought of the partial sums. That makes the computation of my final hull wayyyyyyyy quicker than what it currently is and also reduces scope for errors. That is a nice idea. Thanks.
Now I don't know if I should be happy because my approach was correct or sad because I could not implement it.
I started with binary search as well, but then you can see that actual time doesn't matter much. It seems that the only question is what is the maximum flow you can do such that it's temperature is as given. So you're trying to get that maximum flow by combining original flows. Then the answer is V / maxflow. But I got WA on big dataset :-)
UPD: I think I got where I might be wrong, so now I'm not sure about this flow idea at all.
I got ac using binary search on mincost flow
You can use greedy for computing the maximum flow. More details in this comment.
Yep, my fail was that I started switching on further sources (further in terms of temperature distance) first, rather than first switching on sources which have temperature closest to the one we're trying to get.
My solution that used Simplex-method failed on large test case, but now it got accepted in practice mode after I replaced long double with __float128. Maybe your solution will pass with __float128, too.
Instead of saying that you switch some source on and off, let's say that it's always on, producing water at some rate ri from the interval [0, Ri], that you choose in the beginning.
If the coldest source it too hot, or the hottest source is too cold, then, obviously, it's impossible.
Initially you try setting all rs to maximum. If the water the sources produce is too hot, you start switching the sources off from the hottest. At some point you get to such a state that after switching the hottest running source off, the produced water becomes cold enough or even too cold. At that point you switch the hottest source only partially (you can binary search the correct r).
That's mathematically equivalent to my solution with Minkowski sum, except that I solved a linear equation instead of using binary search.
My solution is based on the greedy approach. First of all, obviously, you may somewhat rephrase the statement and see that instead of opening some source at it's full for some period of time, you can keep it open constantly with some Vi >= 0, Vi <= Vifull. Then, if you have some source with Ti == X, you should open it to it's max. Then, you split the sources in two — the hotter ones and the colder ones and sort them by their temp difference from X. Then, you start picking the current hot one and the current cold in the sorted order, and mixing them in such a proportion that you'll get temp X. After such an operation, one source will be "wasted" completely and the other may have something left — then we'll use that leftovers in next "mix". It may be proven easily that such a mixing order is optimal (you can think of it in such a way — the closer the source temperature is to X, the easier it's for us to utilize this source to it's maximum). It's a pity I got WA on a hard test because of one stupid mistake :(
binary search, find hottest solution, find coolest solution and check X less or equal hottest temperature and greater or equal coolest temperature.
Well, it's over. I was able to participate about the first 50 minutes and last 1 minute (I'm sure there's a problem to make about this :D), so I guess advancing was kind of impossible — but that doesn't mean I should stop trying to do the impossible. Practice makes perfect, after all :D
I was able to participate in first 1.5 hours and, surprisingly, I advanced. I thought that it was impossible, especially given that last year I couldn't even win a t-shirt. And I didn't even solve anything after 1:06. So, advancing in 50 minutes is not that impossible too.
Annnd The T-shirt is gone :(
Problem C is all about König's theorem, I guess...
I used min cut for problem C. You can create 2 nodes per word, where the first node represents "this word is a valid English word" and the second node represents "this word is not a valid French word". The nodes connected to the source correspond to true statements and the nodes connected to the sink correspond to false statements.
You can add infinite-capacity edges to account for the given English and French sentences and the fact that (word A is not French) == TRUE is incompatible with (word B is English) == FALSE when word A and word B are in the same sentence.
Then you connect each word's nodes with 1-capacity edges and you're done.
That is so smart. I thought about min cut but could not model it well.
You can reduce the number of edges greatly by adding a node for each sentence, then connecting the words in that sentence to the sentence node, instead of to each other. With your method, you'd have 1000^2 edges for the first 2 sentences, but with sentence nodes, you only have 1000.
But you do not need to do all that edges for first 2 sentences — just connect words in them to source and sink respectively
I'm trying, but I cannot understand your model in 100%. Could you elaborate on that with some example?
Why downvote? Is my solution the only one that use only bipartite matching? Oo
It's been a while, but do you mind explaining your solution? It seems to be quite different from the others from what I saw in your code.
Oh, I hardly remember the problem...
We can divide words on En, Fr and EnFr. Total amount of words is n, so n - En - Fr = EnFr. If we want to minimize EnFr, we need to maximize En + Fr. Obviously, En and Fr words can't be in the same sentence.
Let's for each word v create two nodes Env and Frv. Env will be taken if v is not En word and Frv will be taken if it is not Fr word. For each sentence s let's connect Ensi and Frsj. Thus to find En + Fr, we need to find maximum independent set in this graph which is the same as complement to the minimum vertex cover which is, by Kőnig's theorem, equals to the maximum bipartite matching.
Problem D is really nice. At first you think that there are myriad of possible patterns, but then you find that there are just 5 "basic" patterns:
The rules are that two patterns of the first kind cannot be adjacent, and two patterns of any other kind cannot be adjacent. Also, some of the patterns require c to be divisible by certain number, and it is necessary to track the rotational symmetry of the resulting pattern (there are 5 symmetry classes). Overall, the solution works in O(r) (can be further reduced to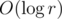 via fast matrix power).
via fast matrix power).
Do you remember, I told you about Burnside's lemma.
It makes life easier here.
Could you post answers your input/output for D-small please? (or outpur for Dsmall-practise)
Output for D-small-prectice:
Thanks
You can download solutions of all contestants and use them to generate outputs on all tests you have.
Yes, sure, but there's a problem that I'll run them on other environment(so they may fail for some reason) and it'll hard to understand
In 99% of cases you'll be just fine ...
39 seconds before the end of contest I was testing this solution — but there was some bug in my DP, so 39 seconds was not enough :(.
In the end I solved A Big/Small, B Small, C Small, D Small — which was enough to get within 500. Definitely not enough to pass next rounds, but this is my best result so far.
I wonder if authors expected that problems B and C can be solved differently using general purpose libraries.
In particular, for B simplex algorithm (KADR confirmed it passes with float_128).
For C, it is formulated as mixed integer programming (confirmed by myself, passes all tests in Large < 1s total, with Gurobi).
Do you think it is a fair advantage to some competitors?
Well. About C, i think any max-flow problem can be solved so.
Of course. But it is a feature of Code Jam that you can use whatever. Which makes such tricks possible.
Also, there is no point in formulating the problem as LP if you already know how to formulate it as a flow:) But I used much simpler IP formulation:
Wk ≥ |Si - Sj| for each pair of sentences i,j with common word k
Very nice! I think it's great to reward creativity of people who try such approaches.
Also, for problem B, bignums were useful (as shown by the fact that I have decided to use them). I think this is the first time since I have started competing at TopCoder in 2003 ;) Maybe they were useful once, but that were extremely simple bignums. This gives advantage to coders using languages which have bignums.
So I had to implement bignums and maxflow (for C), which means that it also gave advantage to coders who have big libraries. I think the contests are nicer when libraries (of algorithms less common than appearing every other match) are not that helpful. (And submitted the answer to A-small for A-large, and was 11 minutes too slow for D-large...)
I had no bignums. Just shift temperature we need to 0.
Yep, this helps. I can get AC with my solution now...
Would you mind explaining why it has reduced precision errors so significantly?
Why is maxflow in the library an advantage? It's literally 10 lines of code, so the library would save just several minutes here.
Huh, several minutes for maxflow — that must have been said by Petr :P. Though maybe Ford-Fulkerson is pretty easy, but easiest really fast flow is Dinic I guess and it demands much more than 10 lines. I copied mine very many times.
But isn't maxflow first thing one is supposed to have in his library? I think that Dinic is algorithm with definitely the biggest product (how often it is needed) * (how long it is)
But why do you need Dinic in this problem? Flow is at most 1000, there are several thousand edges, so O(VE) is enough?
Oh, ok, I understood your reply as you were talking about general case. In this problem indeed we can run Ford-Fulkerson.
I used an extremely simple max flow, but it took more than 10 lines :) Not sure whether it took me more than 11 minutes which I needed for D-large.
I have no Dinic (or any max flow) in my library. I have Marek Cygan's nice implementation, but using someone else's implementation is IIRC illegal in TopCoder, and for other contests I am too lazy to check the rules (and it would feel a bit weird anyway). And rewriting it myself seems to be a pointless activity that I do not want to do. I prefer to complain whenever a problem requires a max flow. :)
Also, what did you use bignums for? After multiplying everything by 10000, we get volumes that are at most 10**8, and temperatures that are at most 10**6, and the maximum intermediate computation is sum(v*t), so 64-bit integers are enough?
Maximum intermediate computation depends on algorithm. I used geo approach and there are some cross products and so on.
I see. I guess the problem rewarded spending some more time thinking before coding. When I was writing the solution, I've also came up with the geometric formulation first, but then realized that the simplest greedy works.
I represent the data as vectors (X,Y) where X = volume, Y = 'energy' = volume * temperature. So X is at most 10**8, Y is at most 10**14. I have to find a linear combination of these vectors so that the goal (X,Y) is achieved.
First, I check whether this is possible, i.e., there are points both below and above the goal. Cross products are 22 digits long. (Obviously this one could be solved easily by looking at the temperatures directly, but somehow I have not noticed this during the contest.)
Then I find out the point where the goal line crosses a polygon. This uses cross products again which are up to NTV^2, and some more calculations which produces numbers of the order of NTV^3 (in my solution, probably could be improved), which are 32 digits long.
Yes, makes sense — thanks for the explanation. Most probably the expressions you compare to 0 have a factor that you can extract, and the rest will fit in int64 (as this solution must be equivalent to the greedy described by Baklazan above).
the main thing on contest — to gain experience
double t1 = (X*V-c[0]*V)/(r[1]*c[1]-r[1]*c[0]);— incorrectdouble t1 = (V*(X-c[0]))/(r[1]*(c[1]-c[0]));— correctI'm doing it wrong with floats again and again :(
Not sure if I ever solve one of this 10^-6 tasks in the contest time :-\
In my case I've just replaced 'double' with 'decimal' and got "Correct".
First formula with read double:
In rough terms, never subtract doubles :)
Available in Gym
How does tourist get such good ideas in such a small time span?
Dammit, if I could find the bug in my min cut solution for C, I would advance to round #3. But still, I got the t-shirt ^_^
Anyone else tried to solve A using min-cost matching?
I solved A-small that way and struggled for the rest of the contest to make it run in time for the large test, but I failed. Ultimately, it ran on about 10 minutes, which wasn't enough, so I submitted some rubbish and got WA. I realized after reading other contestants' codes just how easy problem A was. Very simple greedy. I felt really stupid.
The good side of this is now I've got a very efficient library for min-cost max-flow :)
It didn't occur to you that it might be overkill ( ͡° ͜ʖ ͡°)? Firstly, it was A, secondly people were in fact solving it, thirdly three out of four problems for maxflow will be too much :D (of course I know that third reason is stupid :P). However, I have to say that when I saw samples (before reading statement) I thought "mincost-maxflow", because I recalled one similar problem from TC (of course I got a feeling that this is won't be intended solution since it's A :P). If I recall correctly, difference was that in TC we had to create a cycle cover, not a functional graph/forest of medusas/cycles with trees attached or whatever you call it.
Oddly enough, I didn't stop to think for a moment. I did a horrible contest.
Indeed, there were many things I could have noticed...
I didn't notice any of those things. Instead, I kept struggling and optimizing my library to make it run faster, and that's why I said I felt really stupid after the contest.
To cheer you up — I also didn't qualify to R3 :D
I think that beside algorithmic and coding skills it's also important to keep sane thinking and from your description it's where you mainly failed this time.
Concerning problem Bilingual and time limits in general: I'm finding that a naive bruteforce solution in Python (or Java) times out for the small input (~10 min >> 4 min time limit).
However, I see that some of the solutions submitted by people who got the small input correct during the contest use the same unoptimized bruteforce solution (and also take 10+ min on my computer.)
Could this likely be due to difference of hardware? If so, how much of a constant factor can it make a difference?
For reference, I'm running on a macbook pro retina.
It can easily make a 2X difference. For example, TopCoder has pretty good hardware and solutions run really fast on their servers (when compared to laptops that most people have). My macbook has a 2.4 GHz processor, which isn't impressive at all (there are other factors like caches to consider though).
Another (but very unlikely) difference might be using different compilers — maybe you have python 2.3 (0_o) and the person who submitted the code was using 2.7. Same is true for Java.
The last reason (unlikely as well) might be the particular inputs that those participants got (maybe they were a bit smaller than the reference ones).
So yeah, hardware can make quite a difference.
My PC is 3 times faster than my not-so-new notebook so hardware makes a difference.
C++ is much slower than C++ with -O2. Pypy speeds up python.
Next thing is that one can have eg. 4-threads processor and split input file into 4 files. He has to do some extra job and maybe care about memory but computing will be ~3.9 times faster. So my PC with threads is about 10 times faster than my notebook. It's something.
Can anyone explain the result of the following input of Problem D in Round 2?
I used the dynamic programming approach to solve the problem, but my program failed at the following input for large data:
7 36
The correct output is 16 while my output is 24.
This test case could be reduced to the input of
7 12
where the correct output (by the programs from others) is 16 and my output is still 24.
However, when I try to check the result by hand using the following representation:
Block A2 (period = 1)
333333333333
333333333333
Block B3 (period = 4)
222122212221
212121212121
212221222122
Block C2 (period = 3)
221221221221
221221221221
Block D2 (period = 6)
211222211222
222211222211
Block E1 (period = 1)
222222222222
I get the following results:
Input 4 12
Output 5 (Correct)
1: A2 + C2
2: A2 + D2
3: C2 + A2
4: D2 + A2
5: E1 + A2 + E1
Input 5 12
Output 7 (Correct)
1: A2 + B3
2: A2 + E1 + A2
3: B3 + A2
4: C2 + A2 + E1
5: D2 + A2 + E1
6: E1 + A2 + C2
7: E1 + A2 + D2
Input 6 12
Output 21 (Correct)
1: A2 + C2 + A2 (p3 +) (Note: p3 means period = 3, + means ended with A2)
2: A2 + D2 + A2 (p6 +)
3: A2 + E1 + A2 + E1 (p1)
4: B3 + A2 + E1 (p4)
5,6,7: C2 + A2 + D2 (p6)
8,9,10: C2 + A2 + C2 (p3)
11,12,13: D2 + A2 + C2 (p6)
14,15,16,17,18,19: D2 + A2 + D2 (p6)
20: E1 + A2 + B3 (p4)
21: E1 + A2 + E1 + A2 (p1 +)
Input 7 12
Output 24 (Incorrect)
1: A2 + B3 + A2 (p4 +)
2: A2 + C2 + A2 + E1 (p3)
3: A2 + D2 + A2 + E1 (p6)
4: A2 + E1 + A2 + C2 (p3)
5: A2 + E1 + A2 + D2 (p6)
6,7,8: B3 + A2 + C2 (p12) (3 combinations)
9,10,11,12: B3 + A2 + D2 (p12) (4 combinations)
13,14,15: C2 + A2 + B3 (p12) (3 combinations)
16,17,18,19: D2 + A2 + B3 (p12) (4 combinations)
20: C2 + A2 + E1 + A2 (p3 +)
21: D2 + A2 + E1 + A2 (p6 +)
22: E1 + A2 + C2 + A2 (p3 +)
23: E1 + A2 + D2 + A2 (p6 +)
24: E1 + A2 + E1 + A2 + E1 (p1)
I still cannot figure out what cases among the 24 I listed are duplicated or wrong. Could anybody point it out for me?
Thanks in advance!
What are the 3 combinations for B3 + A2 + C2? I think there is just one up to rotations.
Ahhh I made the terrible mistake that the number of different combinations is min(m,n) — but it's actually gcd(m,n). Thank you for pointing it out!
I know it's too late but can anyone explain the solution of Problem C? I tried hard to understand the above-written ideas but failed to understand. Also, I can't access the dashboard on official site currently.
I remember I solved that live but was getting tle. let me once check is this the same problem I am thinking about or some other