I found this question at http://math.stackexchange.com/.
Let n is a positive integer.
n = p1e1p2e2... pkek is the complete prime factorization of n.
Let me define a function f(n)
f(n) = p1c1p2c2... pkck where ck = ek - 1
Example:
72 = 2332, so f(72) = 23 - 132 - 1 = 2231 = 12
144 = 2432, so f(144) = 24 - 132 - 1 = 2331 = 24
Now let
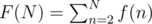
Example: F(10) = 1 + 1 + 2 + 1 + 1 + 1 + 4 + 3 + 1 = 15
Now I want to evaluate F(N) for a fairly large value of N, say 1012. Can I do it without factorizing each number?
It appears quite interesting. I think maybe it requires some kind of inclusion-exclusion, but so far was unable to implement. Any idea how to solve?











If the constraints on this problem are smaller like say N <= 10^6 then it can be solved using sieve only.
Notice that there is small number of different values for f(n).
Yeah, I noticed that. For the squarefree numbers f(n) is always 1. Many numbers are mapped to same f(n). But how can we use this to calculate F(N)?
It seems that it should be possible to calculate for how many numbers f(n) = x holds, given x.
If x = p1^c1 * p2^c2 * .. * pk^ck then n = p1^(c1+1) * p2^(c2+1) * .. * pk^(ck+1) * r1 * r2 * .. * rt where r1..rt are distinct primes different than p1..pk.
So you basically want to know how many square free integers (with no prime factors in p1..pk) are there between 1 and N/(p1^(c1+1) * .. * pk^(ck+1)).
Wow, that is a superb idea. I shall try to implement it. Thanks.
There are 7 square-free numbers <= 10 : 1, 2, 3, 5, 6, 7, 10.
f(n) = x
x can take the values 1, 2, 3, 4
C(x) = No. of integers for which f(n) = x
C(1) = No. of square-free numbers less than (10/1) = 7
C(2) = No. of square-free numbers less than (10/4) = 2
C(3) = No. of square-free numbers less than (10/9) = 1
C(4) = No. of square-free numbers less than (10/8) = 1
Here the sum F(N) is defined for n = 2 to N, so C(1) = 7 — 1 = 6
But we are counting 8 twice, for c(2) and C(4). How can I remove the duplicates?
Yes, those square free numbers should be coprime with x. So you should count 8 only in C(4) because f(8) = 4. You should be able to modify your square-free counting algorithm to not count numbers that have common prime factors with x.
Counting squarefree numbers is a classical problem. The conclusion is really interesting.Check it out HERE.
Use Möbius function, U can do it in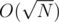 .
.
Let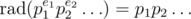 . We know that
. We know that 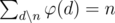 , so
, so
If d divides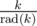 , then
, then 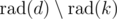 and
and 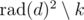 . Let's replace k with
. Let's replace k with 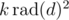 :
:
Now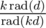 can be replaced with k, as it doesn't change any prime factors included in
can be replaced with k, as it doesn't change any prime factors included in 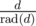 . So again let's replace k with
. So again let's replace k with 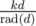 :
:
As there is a bijection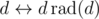 , let's sum over values of
, let's sum over values of 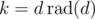 :
:
The sum is over numbers with all prime factors powers greater than 1 (squarefull numbers), I guess there should be about of them, so it should be fast enough for n = 1012.
of them, so it should be fast enough for n = 1012.
Thanks for the wonderful explanation. What does the last term [rad(k)2 k] means? Is it k is divisible by rad(k)2, or just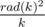 ?
?
There are 2158391 square full numbers < = 1012, so the sum can be indeed calculated in reasonable time.