Hello everyone, this is my editorial for Round #310. I decided to write one since the author of this round didn't have time to do it. Currently, there's only Div2A and Div2B available, and I'll try to write editorial for Div1A and Div1B soon (about Div1C and Div1D, microtony has already written a nice tutorial for them (you can check out here), and Div1E is too difficult for me).
UPD: Div2C-Div1A is available now!
UPD2: Div2D-Div1B is available now!
Div2A — Case of the Zeros and Ones

First, we can come up with a naive solution. While there's still some position i that 'remove-able' ((s[i] = '0' and s[i+1] = '1') or (s[i] = '1' and s[i+1] = '0')), we'll remove s[i] and s[i+1] from the string. However, in the worst case (contain all character '0' first, then character '1' or vise-versa), the complexity is O(n^2) and will surely got TLE.
We should optimize this solution by using stack. Push each character in string s to the stack, and while pushing, check if the top two element of the stack is ('0' and '1') or ('1' and '0') (or we can simply write abs(stack[top]-stack[top-1) = 1). If this happen, remove them from stack (top:=top-2). The answer is the number of character left in the stack.
Solution using Stack: 11816506
Sound a bit too complicated for Div2A, right? There must be a more simple solution. We should notice that if there's still some zero and one in the string, there must be at least one position that 'remove-able'. So, we can remove one character '0' and one character '1' from the string until one type of character run out. We can come up with more simple solution with these analysis: just count the number of character '0' and '1' in the string, and the answer is abs(cnt0-cnt1).
Solution with some analysis: 11830868
Both of the solution has complexity O(n).
Div2B — Case of Fake Numbers
To solve this problem, first, we should notice that after n action, the gear will turn back to the initial state. So, if solution exist, the number of action to get it must be less than n. We can get an solution: just keep performing the action until we get the require structure (answer is 'Yes') or the number of action goes equal n (answer is 'No'). Complexity is O(n^2).
My solution: 11816203
This solution is already fast enough to get AC. But we can easily optimize it further. We can notice that we will need k = (n-a[1]) mod n move to get a[1] equal to 0, so we can just calculate a[i] after k move (whick is (a[i]-k+n) mod n, with i mod 2 = 0 and (a[i]-k+n) mod n, with i mod 2 = 1) and check if this is the required structure. Complexity is now O(n).
The better solution: 11816999
Div2C-Div1A — Case of Matryoshkas
To make thing easier to explain, we will use 'Box' instead of 'Matryoshkas' (Now this problem's name should be 'Case of Box' :D)
Consider the following test:
7 3
2 1 2 6
3 3 4 5
1 7
The following image demonstrate the test:

We know that we can put box a in box b only if box b doesn't contain any other boxes or contained in any other box. So, that mean box b must be alone. So, it would be make sense if we put all the box, which still inside some other box, out (in an appropriate order). However, we don't have to do this with the sequence 1, 2, ..., x since nothing can be put in box 1, and we can just put that sequence of box in box x+1 later. For example, with the above test, the process is described in below picture.
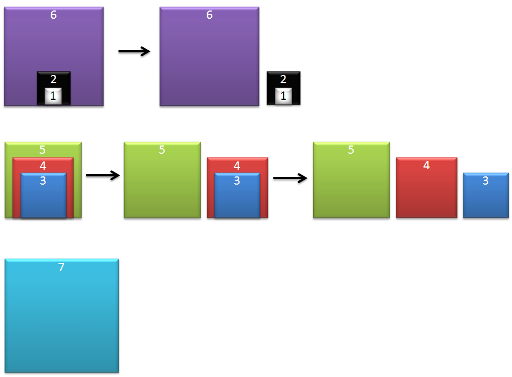
This process take n-(k-1)-x moves.
Then, we can put sequence of box 1, 2, ..., x in box x+1, box x+1 in box x+2, ... box n-1 in box n. For example, with the above test, the process is described in below picture (again).
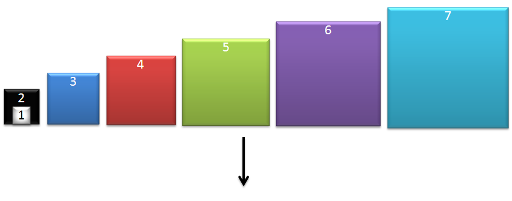
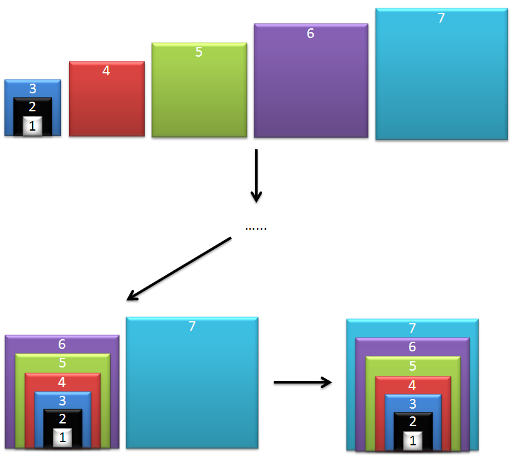
This process take n-x moves.
The final answer is (n-(k-1)-x)+(n-x) = 2*(n-x)-k+1.
My solution: 11821602
Complexity: O(n)
Div2D-Div1B — Case of Fugitive
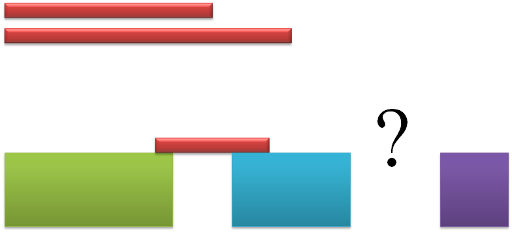
Call b(lb, rb, jth) the j-th bridge to build has required length from lb to rb (inclusive). We know that b[j] = (li[j+1]-ri[j], ri[j+1]-li[j], j). Call c(len, ith) the i-th available bridge that has length of len, with c[i] = (a[i], i). We will also need array ans[i] to store the answer for the i-th bridge to build.
Now, we'll assign ans[i] = -1. Sort b in increase of lb, then increase of rb. Sort c in increase of len.
Now, we will iterate each element of c from left to right. For each c[i], we will consider all the bridge to build that has minimum length less or equal to c[i].len (while(b[j].lb <= c[i].len) ++j) and add them to the 'to_build' list. Then, choose the bridge in 'to_build' list that has the smallest rb and we'll get ans[b[j].jth] = c[i].ith (remember to check that c[i].len <= b[j].rb, too!). At the end, if there's still some ans[i] = -1, then there is no answer. Otherwise, say 'Yes' and print all ans[i].
We'll have O(n^2 + m log m) solution now. To improve this, we need to find the bridge in 'to_build' list that has the smallest rb in O(log n), which can be done by using C++ std::set to store the 'to_build' list.
My solution: 11830446
Complexity: O(n log n + m log m)










Very clear. I'm waiting for the next editorial
Auto comment: topic has been updated by xuanquang1999 (previous revision, new revision, compare).
wow this is the best editorial i've seen till now!
Auto comment: topic has been updated by xuanquang1999 (previous revision, new revision, compare).
it is coming a new era of tutorials.
really nice and illustrative editorial.looking forward to your next editorials . thanks a lot.
if (!s.empty()) { pair<ll, int> top = *s.begin(); if (c[i].fi <= top.fi) ans[top.se] = c[i].se; s.erase(top); } Here in your code if your condition (c[i].fi<=top.fi) is not satisfied then you erase top from set and your for loop on c[] continues skipping that bridge,whereas i think you should check that if for that c[i] is any other suitable gap available in set and then after assigning it to that gap you should continue your for loop.Please clear my doubt.
Since
c[i]is sorted in increase oflen, if currentc[i].lencan't fitj-thbridge, no otherc[i]can do it (all previousc[i]is used). So the code is still right.Thnx,i got it.