Всем привет!
Вообще я думал воздержаться от дальнейших публикаций по палиндромам, так как многие посчитали их слишком навязчивыми. Но задача, о которой пойдёт речь слишком известна и интересна, чтобы не сказать о ней :)
Итак, сама задача: дана строка S. Разбейте её на минимально возможное число палиндромов. Довольно незатейливо, не так ли? Задача довольно популярна. Её можно найти, например, здесь или здесь. Однако, где бы вы её не нашли, ожидаемое решение в лучшем случае будет квадратичным (а то и кубическим). Здесь же будет описано решение этой задачи за  в онлайне относительно приписывания символа в конец строки (т.е. ответ будет получен для каждого префикса). Также будет рассмотрена задача разбиения строки на k палиндромов и её сведение к разбиению на минимальное число палиндромов.
в онлайне относительно приписывания символа в конец строки (т.е. ответ будет получен для каждого префикса). Также будет рассмотрена задача разбиения строки на k палиндромов и её сведение к разбиению на минимальное число палиндромов.
Вообще говоря, это решение сравнительно новое и оно не единственное (другое, впрочем, тоже относительно новое, 2014 года). Его описание можно также найти в статье droptable. В решении будет использоваться дерево палиндромов, о котором можно прочесть в этой статье. За основу будет взята эта реализация.
Итак, приступим :) Для начала рассмотрим следующий наивный алгоритм, работающий за O(n2). Будем поддерживать динамику ans(i) — минимальное число палиндромов, на которое можно разбить префикс строки, оканчивающийся в позиции i. Для её пересчёта будем строить дерева палиндромов строки и на каждом шаге проходить по всем cуффикс-палиндромам текущего префикса, переходя от вершины к её суффиксной ссылке.
for(v = last; len[v] > 0; v = link[v])
ans[i] = min(ans[i], ans[i - len[v]] + 1);
Чтобы решить задачу быстро, введём две новые величины, которые будут храниться в вершинах дерева палиндромов — разность вершины diff(v) = len(v) - len(link(v)), а также серийную ссылку slink(v). Серийная ссылка будет вести из вершины v в вершину u, соответствующую максимальному суффикс-палиндрому v, для которого верно diff(v) ≠ diff(u). Легко видеть, что её можно пересчитывать при создании новой вершины таким образом:
if(diff[v] == diff[link[v]])
slink[v] = slink[link[v]];
else
slink[v] = link[v];
Утверждение 1: путь по серийным ссылкам имеет длину  . Оставим его доказательство любопытному читателю в качестве упражнения.
. Оставим его доказательство любопытному читателю в качестве упражнения.
Зная данный факт, хочется иметь алгоритм следующего вида:
Начиная с максимального суффикс-палиндрома (last), быстро "прорелаксируем" ответ вдоль всех суффикс-палиндромов до серийной ссылки, после чего перейдём по серийной ссылке и повторим процедуру. Легко видеть, что таким образом все суффикс-палиндромы будут учтены. Научимся быстро обрабатывать описанное множество палиндромов (назовём его серией). Для этого нам понадобится
Утверждение 2: пусть мы рассматриваем в описанном алгоритме суффикс-палиндром v и link(v) ≠ slink(v). Тогда предыдущее вхождение link(v) в строку было в позиции i - diff(v), при этом в этой позиции не существует суффикс-палиндрома длины len(link(v)) + diff(link(v)), то есть, link(v) было началом серии.
Доказательство: Так как суффикс палиндрома является для него и префиксом, мы можем указать вхождение link(v) в указанной позиции, как префикса текущего суффикс-палиндрома. Покажем, что не могло быть вхождения link(v) между i и i - diff(v). Допустим, оно есть. Тогда пересечение вхождения в этой позиции и в позиции i - diff(v) также является палиндромом (т.к. оно само является границей палиндрома) длины большей, чем len(v) - 2·diff(v). Отсюда следует, что diff(link(v)) ≠ diff(v), противоречие с утверждением.
Покажем, что мы не могли во вхождении с позиции i - diff(v) дописать слева diff(v) символов и получить палиндром. Пусть v = DTDT, link(v) = TDT = DT. Отсюда можно видеть, что если мы дописали к строке слева diff(v) символов и получили палиндром, то дописанные символы были равны D. Но в силу того, что DT — палиндром, получаем, что DDTDT также палиндром. Следовательно, v не могло быть началом серии. На полученном противоречии доказательство утверждения заканчивается.
Основываясь на утверждении 2, заведём следующую вспомогательную динамику: Пусть series(v) — серия, начинающаяся в вершине v, тогда значение динамики в ней равно
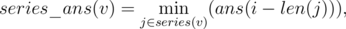 где i — последняя (из уже рассмотренных) позиция в строке, в которой эта вершина соответствовала самому длинному палиндрому серии. Можно заметить, что когда мы находимся в позиции i, то series_ans(link(v)) в силу утверждения 2 охватывает все интересующие нас значения, кроме одного, в котором длина суффикс-палиндрома равна len(slink(v)) + diff(v), то есть, просматриваются все суффикс-палиндромы, кроме наименьшего в серии. Его можно рассмотреть отдельно.
где i — последняя (из уже рассмотренных) позиция в строке, в которой эта вершина соответствовала самому длинному палиндрому серии. Можно заметить, что когда мы находимся в позиции i, то series_ans(link(v)) в силу утверждения 2 охватывает все интересующие нас значения, кроме одного, в котором длина суффикс-палиндрома равна len(slink(v)) + diff(v), то есть, просматриваются все суффикс-палиндромы, кроме наименьшего в серии. Его можно рассмотреть отдельно.
Итого имеем алгоритм такого вида:
for(v = last; len[v] > 0; v = slink[v])
{
series_ans[v] = ans[i - (len[slink[v]] + diff[v])];
if(diff[v] == diff[link[v]])
series_ans[v] = min(series_ans[v], series_ans[link[v]]);
ans[i] = min(ans[i], series_ans[v] + 1);
}
Очевидно, он работает за O(nt), где t — максимально возможная длина "серийного пути", то есть,  .
.
Интересна также уже упомянутая задача разбиения строки на k палиндромов. Научимся решать её.
Утверждение 3: если строку можно разбить на k ≤ n - 2 палиндромов, то её можно разбить и на k + 2 палиндромов.
Действительно, если в строке есть хотя бы один палиндром длины ≥ 3, то мы можем "отцепить" от него две крайние буквы. В противном случае мы можем найти любую пару палиндромов длины 2 и разбить каждую.
Отсюда видно, что для ответа на вопрос о разбиении на k палиндромов, нам достаточно узнать минимальное чётное и минимальное нечётное число палиндромов, на которое можно разбить строку. Это легко сделать, модифицировав приведённый алгоритм (будет две динамики — для чётных и нечётных длин, а их пересчёт будет идти перекрёстно).
Пример программы, выводящей для каждого префикса минимальное число палиндромов, на которое его можно разбить: #xE2k6Y











Лучше бы с Huyum_nik'ом на море съездил)))
Так он не позвал(
Не по братски вообще
Thank you so much..
Отличный разбор, мне он Оооочень помог! Удачи Вам !
Не думал, что в открытке этого года будет такое в подзадаче