micklepru's blog

Bitmask DP doing some magic
By micklepru, history, 9 years ago, In English

UPD: Thank you for your help, sort it out for myself. Hope this may help someone else now.

Hello, Codeforces!

I ask you to help me understanding how does the algorithm work.

Here is the problem. Basically we have two integers N and M, we need to find how many numbers obtained by rearranging digits of N are divisible by M.

So naive solution is just go through all permutations of digits of N and check all of them. That gives us N! operations, which is unacceptably slow. Intuitively, we must go through all permutations anyway. And I am very confused about how do we not.

We use bitmask DP: dp[i][j] — amount of numbers, obtained by permutation some digits of N(specified by bitmask i), and remainder after diving it by M is j. For example N=12345, dp[01101][2] — amount of numbers, constructed with 2,3,5 (such as 352), and after division by M remainder is 2 (M=50, 352%50==2). For each bitmask i we iterate(variable k) through all unused yet digits((i & 1<<k)==0) and add it to the end of every permutation(i | 1<<k). Old permutations gave remainder j, now it will be (j*10+N[k])%M, where N[k] is k-th digit of N. So we increase dp[i | 1<<k][(j*10+N[k])%M] by dp[i][j].

Here is the code to make it easier: 12205724 Note: timesRepeat is used to eliminate duplicate permutations regarding repeated digits in N. (i||N[k]) is to get rid of leading zeros

Using DP, we descend from N! to (2^N)*N, which gives us accepted.

Consider the solution: seems like we iterate through every permutation. For example, bitmask 0110 can be obtained as 0100 adding third digit to the end or 0010 adding second digit to the end. I cannot understand how are we doing less work, but logically we go over every permutation.

Maybe it is stupid question, but I am really confused. Please help me to sort it out and tell when do we use such method. Can we use it to any kind of permutations?

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Since the possible mods are limited, if we used 4 numbers for example and our current modulo is 3 ,and another permutation of those 4 numbers gives also modulo 3, in the naive solution if we have 18 digits we would try the left 14 digit permutations twice, but the answer of this subproblem is saved in the DP table you don't have to recalculate it , you just add the numbers as you calculated them before!, So the complexity is cut to the number of subproblems you need to calculate!

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

First of all, the actual complexity is 2N * M * N.

I'll try to explain why you don't need to go through all the permutations, then maybe the DP solution will start making sense. The key idea, like in every other DP problem, is that you don't need to know the exact intermediate state (in this case, the prefix of the permutation) to be able to compute the answer for the whole problem. Instead, you can define features of intermediate state that are important for your problem -- in this case, the subset of digits that have been used and the remainder modulo M that this prefix has. Two prefixes that consist of the same subset of digits and have the same remainder will "behave" in the same way with regard to the function you are trying to compute (i.e., the number of permutations that divide by M).

This probably didn't make so much sense to you, so let's look at an example. Suppose M = 7 and N = 1122334. Look at the following two prefixes, both comprised of (multi)set {1, 2, 2, 3, 3}: 31232 and 12332. They both have remainder 5 modulo M = 7. You obviously have the same set of numbers that can be appended to these prefixes. On the other hand, for any digit X, when you append it to either of this prefixes, the resulting remainder will be the same for both of them. For example X = 1: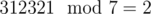 , 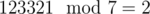. If this confuses you, think about the rules of how modulo operation behaves for multiplication: 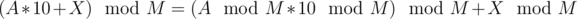, therefore the exact value of A does not matter, only 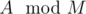does. Hence, you don't care any more if it was prefix 31232 or 12332 that you were trying to complete, the number of ways to complete it will be the same. This means that you could count how many prefixes are there comprised of {1, 2, 2, 3, 3} with remainder 5 modulo M and see in how many ways any of them can be completed and multiply these two numbers, instead of computing the number of ways to complete every one of these prefixes.

Hope this helps a bit.

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

You write: "For example, bitmask 0110 can be obtained as 0100 adding third digit to the end or 0010 adding second digit to the end." Now consider the next step: the bitmask 0111 can among others be obtained from 0110, and now your two ways of reaching 0110 are taken care of using one operation only.

It might help to look at the following somewhat silly DP to calculate the number of permutations:

dp[0] = 1;
for (int mask = 1; mask < (1 << N); mask++)
    for (int i = 0; i < N; i++)
         if (mask & (1 << i))
             dp[mask] += dp[mask ^ (1 << i)];

Here, dp[mask] is the number of ways to obtain mask, and dp[(1 << N) - 1] is of course N!.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in this comment it is well explained. however, this maybe a hard example for dp magic i suggest you to see this problem. it is somehow easier, at least no need to mask anything here. in short the problem states that you have(n <= 10000) number and (k <= 100) after you read this n numbers you have to say whether we can put operations between the numbers (+, -) that the final result will be divisible by k or not. as a naive solution we have (n-1) gabs between the numbers and we are to choose to put + or - this is 2^(n-1) possibilities! then for each possibility we calculate the result and see if it's divisible or not. However we can see that we are not interested in the final result, we are interested in its modulo on k, and from there we can see how dynamic programming will work just define state dp[i][j] = can we put operations between numbers (0 ... i) to reach modulo j on k, and the transition is simply dp[i][j] = dp[i-1][(j+A[i])%k] || dp[i-1][(j-A[i])%k], so we reduced O(2^(n-1)) to O(n*k) !

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can Anybody show me the whole procedure for following input?

Input: 123 3 Output: 6

→ Reply