In this problem one need to check whether it's possible to choose k elements from array A and m elements from array B so that each of chosen element in A is less than each of chosen elements in B. If it's possible then it's possible to choose k smallest elements in A and m largest elements in B. That means that in particular, k-th smallest element of A is less than m-th largest element in B. So, if A[k] < B[n - m + 1] then the answer is "YES" and if not, then the answer is "NO".
Problem author: zeliboba.
Problem developers: riadwaw, Kostroma.
Solution code: 12873382.
First of all the problem may be solved for buy orders and sell orders separately.
The easiest soultion is to use structure like std::map or java.lang.TreeMap. To aggregate orders we just add volume to the corresponding map element: aggregated[price] += volume.
After that we should extract lowest (or largest) element from map s times (or while it's not empty).
Complexity of this solution is O(nlogn).
It is also possible to solve the problem without data structres other than an array. You should just maintain at most s best orders in sorted order and when adding another order you insert it in appropriate place and move worse elements in linear time of s. Complexity of this solution is O(sn).
Problem authors and developers: ArtDitel, yarrr.
Solution code: 12873385.
Let's count the number of ways to form a triple which can't represent triangle sides, and then we subtract this value from 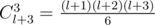 — the total number of ways to increase the sticks not more than l in total. This number is obtained from partition of l into 4 summands (la + lb + lc + unusedl = l), or can be counted using a
— the total number of ways to increase the sticks not more than l in total. This number is obtained from partition of l into 4 summands (la + lb + lc + unusedl = l), or can be counted using a for loop.
Now we consider triples a + la, b + lb, c + lc, where la + lb + lc ≤ l, la, lb, lc ≥ 0. Fix the maximal side, for example it would be a + la. We'll have to do the following algo for b + lb and c + lc in the same way. The triple is not a triangle with maximal side a + la if a + la ≥ b + lb + c + lc. If we iterate over la between 0 and l, we have the following conditions on lb, lc:
lb, lc ≥ 0. So, non-negative integers lb, lc should be such that lb + lc ≤ min(a - b - c + la, l - la). If we denote this minimum as x than we can choose lb, lc in 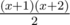 different ways (again we divide x into three summands: lb, lc and some unused volume). Also when we fix lb, there are x - lb + 1 ways to choose lc, so the overall number of pair lb, lc is
different ways (again we divide x into three summands: lb, lc and some unused volume). Also when we fix lb, there are x - lb + 1 ways to choose lc, so the overall number of pair lb, lc is
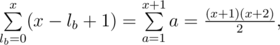
so we obtain the same formula.
To sum up, we need to iterate over the maximal side and over the addition to that side, then write these formulas, and subtract the result from the total number of different additions to the sides. The complexity of the solution is O(l).
Problem author: Kostroma.
Problem developers: Kostroma, riadwaw.
Solution code: 12873406.
We can divide all indices [1;n] into groups by their remainder modulo k. While counting 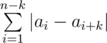 , we can consider each group separately and sum the distances between neighbouring numbers in each group.
, we can consider each group separately and sum the distances between neighbouring numbers in each group.
Consider one group, corresponding to some remainder i modulo k, i.e. containing aj for 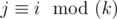 . Let's write down its numbers from left to right: b1, b2, ..., bm. Then this group adds to the overall sum the value
. Let's write down its numbers from left to right: b1, b2, ..., bm. Then this group adds to the overall sum the value
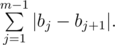
We can notice that if we sort b1, ..., bm in non-decreasing order, this sum will not increase. So, in the optimal answer we can consider that numbers in each group don't decrease. Furthermore, in that case this sum is equal to |bm - b1|.
Now consider two groups b1, ..., bm and c1, c2, ..., cl, both sorted in non-decreasing order. We claim that either b1 ≥ cl or bm ≤ c1, i.e. segments [b1, bm] and [c1, cl] can have common points only in their endpoints.
Why is this true? These groups add |bm - b1| + |cl - c1| to the overall sum. We consider the case c1 ≥ b1, the other is symmetric. If c1 < bm, then swapping c1 and bm will not increase the values these groups add to the answer, since the right border of b group moves to the left, and the left border of c group moves to the right. So, c1 ≥ bm in that case, and the assertion is proved.
Now we know that the values in each group should from a continuous segment of the sorted original array. In fact, we have 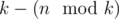 groups of size
groups of size 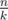 (so called small groups) and
(so called small groups) and 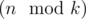 groups of size
groups of size 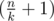 (so called large groups). Consider the following dynamic programming: dp[L][S] — the minimal sum of values added to the answer by L large groups and S small groups, if we choose the elements for them from the first
(so called large groups). Consider the following dynamic programming: dp[L][S] — the minimal sum of values added to the answer by L large groups and S small groups, if we choose the elements for them from the first 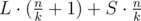 elements of the sorted array A. There are no more than O(k2) states, and each transition can be made in O(1): we choose large or small group to add and obtain the number it adds to the sum by subtracting two elements of the sorted array. The answer for the problem will be in
elements of the sorted array A. There are no more than O(k2) states, and each transition can be made in O(1): we choose large or small group to add and obtain the number it adds to the sum by subtracting two elements of the sorted array. The answer for the problem will be in 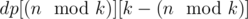 .
.
The overall complexity of the solution is 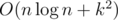 . We can note that in pretests
. We can note that in pretests 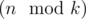 was quite small, and some slower solutions could pass, but they failed on final tests.
was quite small, and some slower solutions could pass, but they failed on final tests.
Problem author: zeliboba.
Problem developers: Kostroma, riadwaw.
Solution code: 12873418.
Firstly let's assign values to variables occurring in our fomula only with negation or only without negation. After that we can throw away the disjuncts which contained them, since they are already true, and continue the process until it is possible. To make it run in time limit, one should use dfs or bfs algorithm to eliminate these variables and disjuncts.
So now we have only variables which have both types of occurrences in disjucnts. Let's build a graph with the vertices corresponding to disjuncts, and for each varible a make an edge between the disjuncts that contain a and !a. Now we should choose the directions of edges in this graph in such a way that every vertex has at least one incoming edge.
We can notice that if some connected component of this graph is a tree, the solution is not possible: on each step we can take some leaf of this tree, and we have to orient its only edge to it, and then erase the leaf. In the end we'll have only one vertex, and it'll not have any incoming edges.
Otherwise, take some cycle in the component and orient the edges between neighbouring vertices along it. Then run dfs from every vertex of the cycle and orient each visited edge in the direction we went along it. It is easy to easy that after this process every vertex will have at least one incoming edge.
So, we should consider cases with the variables which values can be assigned at once, than construct a graph from disjuncts and variables and find whether each connected component has a cycle. If so, we also should carefully construct the answer, assigning the remaining variables their values, looking at the directions of the edges in the graph. The overall complexity is O(n + m).
Problem author: zeliboba.
Problem developers: Kostroma, zeliboba, yarrr.
Solution codes: 12873432 (linear solution), 12873446 (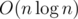 ), 12873456 (matching solution).
), 12873456 (matching solution).
Let's suppose for each dormitory from Q query we already know the last raid moment.
When task will be much easier: we can throw away M and Z queries and to get right answer we should subtract two values: people count in dormitory right now and same count in a last raid moment.
On this basis, we have such plan:
- For each Q query let's find the last raid moment using M and Z queries.
- Find people count in two interesting moments using U and A queries.
- Calculcates the final answer.
Let's try to solve the first part.
We want to make such queries on disjoint sets:
- Merge two sets (M query).
- Assign value time for all elements in particular set (Z query).
- Get value for a particular element (Q query).
To solve this task we'll use a well-known technique: "merge smaller set to bigger".
We'll maintain such values:
- elements — set elements.
- set_id — for each element their set id.
- last_set_update_time — last moment when assign operation has occurred for each set.
- last_update_time — last moment when assign operation has occurred for each element.
- actual_time — moment of time when last_update_time was actually for the element.
Let's focus on actual_time value.
It's obvious that when we merge two sets each element can have a different last assign moment. But after first assignment all elements from any set will have the same value. So the answer for Q query for element i from set s: If last_set_update_time[s]=actual_time[i] then last_update_time[i] else last_set_update_time[s]
For each Z query you should just update last_set_update_time array.
It's easy to maintain this values when you merge two sets:
Let's suppose we want to merge set from to set to. For each element from set from we already know last assign time. So just update last_update_time with this value and actual_time is equal of last assign operation for set to.
The second part of the solution is the same as first one.
O(n * lg(n) + m) time and O(n + m) memory.
Problem author: ArtDitel.
Problem developers: yarrr, gchebanov, Kostroma.
Solution codes: 12873477 (solution, described in the editorail), 12873469 (solution with treaps).
571E - Геометрические прогрессии
If intersection of two geometric progressions is not empty, set of common elements indexes forms arithmetic progression in each progression or consists of not more than one element. Let's intersect first progression with each other progression. If any of these intersections are empty then total intersection is empty. If some of these intersection consist of one element, then we could check only this element. Otherwise one could intersect arithmetic progressions of first progression indexes and take minimal element of this intersection. The remaining question is how intersect two geometric progression? Let's factorise all numbers in these two progressions and find set of appropriate indexes for every prime factor in both progressions. These progressions one need intersect both by values and by indexes.
Problem author: zeliboba.
Problem developers: zeliboba, yarrr, gchebanov.
Solution code: 12873480.











Why you don't prepare editorial before contest?...But thanks at all... ;)
Auto comment: topic has been updated by Kostroma (previous revision, new revision, compare).
Order Book: "You should just maintain at most s best orders" Why?
In the beginning it was pretty hard for me to think about how geometric progressions behave and how they can intersect etc., but when I thought about them as vectors in everything turned out to be obvious immediately :).
everything turned out to be obvious immediately :).
Correct, it simplifies some considerations.
tks author, this is great contest. But i only solve 2 Pro :(
For problem 571A — Lengthening Sticks it looks like there is a typo, it should be (l+1)(l+2)(l+3)/6 not (l+1)(l+1)(l+2)/6.
Thanks, it has been corrected
In Div1-A, can anyone explain why the total number of ways to increase the sticks not more than l in total is C(3; l+3)?
make l in x1,x2,x3 but it's seen that x1,x2,x3>=0,it's hard:( so,let's set y1=x1+1,y2=x2+1,y3=x3+1. then the question becomes:make l+1+1+1 in y1,y2,y3 but the difference is that y1,y2,y3>=1! and we can ues many ways to prove that is C(3,l+3) then the question is done,hope to help you =)
"prove":There're (l+3) numbers,we want to split it into 3 (2 + 1) parts,and each part has at least 1 numbers.Imagine to put 3 clapboards in the (l+3)blanks,that's C(3,l+3)...
I think that's what xuanquang1999 is asking for, and your comment didn't explain this.
And as explained on the other thread, you can use stars-and-bars technique to count such partitions.
I can explain with multiset combinations.
From wiki: There are Cn+k-1,k ways to choose k elements from a set of n elements if repetitions are allowed. See Multiset (https://en.wikipedia.org/wiki/Multiset)
Using above formula for the number of multiset combinations: n is your l+1 (including 0), k is 3 and k elements are l1, l1+l2, l1+l2+l3 — note that repetitions are allowed. So your total number is Cl+3,3
571B... I almost solved it
I have to satisfy with 571A
Will be authors solution?
Can someone help me to understand the solution of 571B - Minimization ?
i am also not able to understand explanation of 571B — Minimization. Can some one explain in simple terms wit some sample examples.
Thanks
C(3,l+3)=(l+1)(l+2)(l+3)/6?
but the Solution says C(3,l+3)=(l+1)(l+1)(l+2)/6? :)
It's a Combinatorial mathematics formula.
Here is my solution for Div1 C. After construct the graph as you described above, then find a maximum matching in this bipartite graph. If the size of found matching equals to the number of disjucts the answer is YES, otherwise it's NO.
can you explain your solution in more detail? i solved it like discribed in editorial, but i don't understand why this graph is bipartite and how to apply maximum matching to this problem.
The graph is bipartite because each edge join a literal and a disjuct.
There could be 4.105 edges in the graph. What is your bipartite matching complexity?
Actually I don't know the exact complexity of my code. I copy the code from an algorithm book, and use that code to got accept the problem. You can see the code here: http://codeforces.com/contest/571/submission/12663732. [WARNING: really bad implementation).
My solution for Div2 C.Let's run a for loop from i=1 to l.Calculate s=(a+b+c+i)/2. Notice that a non-degenerate triangle is only possible iff length of all sides is strictly smaller than s(semi-perimeter of triangle). So now the question reduces to find the number of integral solutions of x1+x2+x3=(a+b+c+i) such that a<=x1<=s,b<=x2<=s,c<=x3<=s (if (a+b+c+i)%2=0 then decrease s by 1) which is nothing but finding coefficient of x^i in (1+x+x^2+.....+x^(s-a))*(1+x+x^2+....+x^(s-b))*(1+x+x^2+...x^(s-c)).
I too was thinking it this way, but implementing this looked very cumbersome. I saw that people did it in less than 10 minutes, which meant that there existed a simpler solution. I spent all my time figuring what it could be, and unfortunately, failed miserably. :P
yes the implementation part was really bad. You can see my code here http://codeforces.com/contest/572/submission/12664073 . If someone has a better implementation using the same logic do reply.
Would you explain about last part please?
Shouldn't it be a <= x1 < s instead of a <= x1 <= s, and same for x2 and x3? Otherwise it seems "non-degenerate triangle is only possible iff length of all sides is strictly smaller than s" is not fulfilled?
Oh, understood after seeing the implementation. He said "if (a+b+c+i)%2==0 then decrease s by 1", which means if it is odd, it takes care of itself.
In Div-2 D / Div-1 B : Can anyone explain the proof of why values in each group should from a continuous segment of the sorted original array? Can't seem to get it from the editorial.
Each group is sorted and any two group can have common points only in their endpoints.
Suppose not. Assume each group is in sorted order. Then as you can see in the pic, at least one of the end points of one groups, lays within the other group (The picture shows a particular condition of two groups. For any other situation a similar observation can be made).
So in this case , let's move x6 (maximum) from group X to group Y , and y1 (minimum) from group Y to X. If you compare the total length of the narrower arrows which represent the "cost" of each group before and after the swapping of two elements, you'll see that this kind of change in the groups will always lead to a better answer.
Nicely explained. Thanks! :)
What does author mean by the states ? And how is that O(k2)? Can you also explain how to implement the algorithm. I am stuck here. Thanks.
"States" means "dynamic programming algorithm states". If you're not familiar with the concept, you can learn more about it and solve some easier problems Here (Number 24) first.
Also make sure you have understood the part about big groups and small groups in the editorial (feel free to ask if you couldn't).
The DP states in this problem are defined as this: We have chosen "i" small groups and "j" big groups, so dp[i][j] will be equal to the minimum "cost" for choosing such i "small" + j "big" groups. dp[0][0] = 0 is the only trivial case and dp[n][m] (where n and m are the total number small and large groups that need to be chosen respectively) will contain the answer after the execution of the dynamic programming algorithm.
The dp transitions go like this : Suppose we're on state(i , j) now. We'll try to update states (i + 1, j) and (i , j + 1). In other words, on each step we are trying to choose either a small or a large group, until we reach the desired state which is (n , m).
Based on my previous comment we know that each group is consisted of a contiguous segment of the input array in sorted order. Therefore in the dp transitions we'll choose numbers from the start of the list. That is when choosing numbers that are going to be placed in a small group( (i ,j) -> (i +1 , j) ), we will choose the first "al" numbers in the sorted array which are not chosen yet ("al" is the number of elements in a small group) and we will choose the first "bl" elements otherwise ( (i,j) -> (i , j + 1) ).
But how do we know that how many elements of the array have been chosen ? Since the number of elements in each of the two kinds of groups is fixed, having i and j, we'll be able to find how many elements have been used, and we can choose "al" or "bl" elements from there. The extra cost choosing these elements adds to the total cost is the difference between the first and the last elements (in non-decreasing order) in the group. So the transitions would be like this if we are on (i,j) : (dp[i][j] is the minimum cost of choosing i small groups and j large groups , al is the size of the small groups and bl is the size of the large groups)
if dp[i][j] + cost of choosing the first "al" elements starting at the index al*i + bl*j (which is the last chosen number) makes up for a better cost than the current dp[i+1][j], update it.
if dp[i][j] + cost of choosing the first "bl" elements starting at the index al*i + bl*j (which is the last chosen number) makes up for a better cost than the current dp[i][j+1], update it.
code
Thank you so so much. I just can't tell you how helpful this has been. I was stuck here for like over a day now.
No problem. I hope you can solve it now.
I still don't understand how does it work. I understand that we need to look at all the combinations formed by sequence of small and large segments. If we encode them as 0s and 1s we should look for a combination like 1000101110101011 of length k that will minimize the sum. I do not understand, how are we skipping all these combinations...
Note that swapping c1 and bm doesn't mean swapping these two elements themselves; it means inserting the element into another group. The group is always in non-decreasing order!
Div-2 C : How to convince or prove that, the procedure listed in the solution in exhaustive. That is sum of three inverse selection is indeed removing all the triangles with non-positive area.
By Triangle inequality we have:
It has positive area if:
(A < B+C) && (B < A+C) && (C < A+B)
Negation: It has a non-positive area if:
(A >= B+C) || (B >= A+C) || (C >= A+B)
Then, from all the triangles calculated adding 0 <= x+y+z <= L, substract these with non-positive area:
(A+x >= B+y+C+z) || (B+x >= A+y+C+z) || (C+x >= A+y+B+z)
The ways to sum L with 3 numbers:
F(0) = 1
F(L) = L+1+F(L-1).
A implementation: 12711452
https://www.khanacademy.org/math/geometry/basic-geometry/triangle_inequality_theorem/v/triangle-inqequality-theorem#
Register on khanacademy, then study and master the concept. It was very useful for me.
MY EXPLANATION OF PROBLEM "LENGTHENING STICKS" the conditions for the triangle with sides a,b,c which can be increased by length La,Lb,Lc with the restriction that limit of combined increase should be less than equal to L having positive area is-
we basically need to take two things in account to solve the problem
1) Calculate All Possible Combinations Of The Lengths Of Sides That We Can Have :: Mathematical formula of which and explanation can be found out here-
http://math.stackexchange.com/questions/192670/n-unlabelled-balls-in-m-labeled-buckets therefore considering the first testcase of 1 1 1 2 , total possible combinations of side lengths we can have is 10 = (2+1)(2+2)(2+3)/6 ;
2) start off with one given side and keep on increasing till the increase in its side becomes equal
to L because that's the maximum possible increase we can have.
let us take an example to understand this further- In above mentioned case we represent the sides by (1,1,1) -> (a,b,c). we start off with side 'a' of length =1; we first increase the size of this side by La=0;
now we look at our condition
1) a+La < b+c (1+0)<(1+1)
so this condition holds true, so even if we increase the lengths of 'b' and 'c' the condition will
remain true so this will never result in any non-positive area(degenerate) triangle.therefore we further increased 'a' by 1 .Therefore La=1 and again look at our condition
2) a+La >= b+c (1+1)>=(1+1)
This does not satisfy our condition of positive area triangles. now since we have satisfied one condition of degenerate triangle we look further into different possibilities of Lb and Lc with the
restrictions that degeneracy should be maintained and total combined increase should be less than equal to L.
This gives rise to two more conditions
1) a+La >= (b+Lb) + (c+Lc) ( lb + lc<=a+la-(b+c) (in our case this equals to 0 (1+1-1-1) ) )
2) la+lb+lc<=L ( lb+lc<=L-la ( (in our case this equals to 1 (2-1) ) )
taking both into account we get lb + lc<=min(a + la- (b + c) ,L-la);
let the minimum be x (in our case this equals to 0) again using our combination knowledge we get that equal (x+1)*(x+2)/2 (in our case this equals to 1) this way we got all possibility of degenerate triangles with side 'a' as '2' (a+la). now we subtract
this from our total combinations.(10-1=9) Now we further increased the length of a by 1 so that a becomes '3' (a+La=1+2) and again look at our conditions
3) a+La >= b+c (1+2)>=(1+1)
this does not satisfy our condition of positive area triangles. now since we have satisfied one condition of degenerate triangle we look further into different possibilities of Lb and Lc with the
restrictions that degeneracy should be maintained and total combined increase should be less than equal to L.
This gives rise to two more conditions
1) a+La >= (b+Lb) + (c+Lc) ( lb + lc<=a+la-(b+c) (in our case this equals to 1 (1+2-1-1) ) )
2) la+lb+lc<=L ( lb+lc<=L-la ( (in our case this equals to 0 (2-2) ) )
taking both into account we get lb+lc<=min(a+la-(b+c),L-la);
let the minimum be x (in our case this equals to 0) again using our combination knowledge we get that equal (x+1)*(x+2)/2 (in our case this equals to 1) this way we got all possibility of degenerate triangles with side a as '3'(a+la). now we subtract
this from our total combinations.(9-1=8) Doing the same thing for the 2 more sides we get the number of degenerate triangles=6(2*3)
THIS IS BASICALLY WHAT WE ARE DOING IN OUR CODES.
NOW WE NEED TO LOOK AT TWO MORE IMPORTANT THINGS-
1) All Degenerate Triplets are Unique - since for degeneracy (a'=a+la, b'=b+lb, c'=c+lc) 1) a'>=b'+ c' (a'>=b' and a'>=c') 2) b'>=a'+ c' (b'>=a' and b'>=c') 3) c'>=a'+ b' (c'>=b' and c'>=a') the second condition part in brackets of all three conditions can only be satisfied simultaneously if triplets are unique.
2) They Cover all the Possibilities since for every side we starting from its original length and going till maximal possible length we are covering all its possibilities and since we are doing this for all three sides we are
getting all possible triplets
Can't there be a situation when 2 triplets come to be same ? Like if first we have a and then we increase b; and in another case where we first have b and then increase a. Won't the triplets be equal?
can anyone explain tutorial of Minimization with an example, so that it can be more clear ??
I div1/E 1st test case:
2
2 2, progresion 2,4,8,16,...2*2^x=2^(x+1)
4 1, progresion 4,4,4,4,...4*1^x=4
I'm not realy clear how is answer 4.Have I misunderstood something?
I got it now... f(x) is needed not x ...
Solution for Div 1 B is wrong isn't it?
For example, for this case
Clearly, we can see the solution is from segment [0, 1] and [2, 12], which give result = 0, but if we assume that all groups should belong to a continuous segment (as stated in the solution), so we can only obtain result = 1, which is wrong.
The permutation for correct result should look like:
If N=13 and K=7 the permutation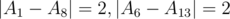 and other terms are equal to 0.
and other terms are equal to 0.
-1 1 1 1 1 1 0 1 1 1 1 1 -1leads to an answer of 4, becauseSorry, wrong permutation, updated. It should be:
The solution described in the editorial will lead to exactly the permutation you provided. Here's how.
We want to split all these numbers into 6 groups of size 2 and 1 group of size 1. All these groups are going to be independent because they are not going to intersect with each other in the final permutation.
The described DP solution leads to the following partitioning:
[-1, -1], [0], [1, 1], [1, 1], [1, 1], [1, 1], [1, 1].If we want to construct the final permutation from this partitioning, we would first put 0 into position 7, because that's where the group of size 1 starts. We'd then fill out the rest of the groups of size 2:
[-1, -1]into positions 1 and 8,[1, 1]into positions 2 and 9, and so on.In Div1-E,
What does it mean to "intersect both by values and by indexes"? How to do it? How to combine progressions from primes?
Finally AC. The tests are very good, catched so many different bugs:
Auto comment: topic has been updated by Kostroma (previous revision, new revision, compare).
For Problem D in Div2. why we have K-(n mod K) groups of size n/k (so called small groups) and (n mod k) groups of size (n/k+1) (so called large groups)? please explain anyone ....
Any idea why C can be solved like this: 12659862
Hm, taking smallest clause and assigning first variable to satisfy it. There should be counterexample..
I don't feel like reading that code, but what I can tell is that it is probably doing something smarter than what you've described, because that way this would be a counterexample:
4 3 2 1 2 2 2 3 2 3 1 3 -1 -2 -3
but custom invocation says it is not.
If it is possible to use a variable (and is negation) more than twice, a simple 2SAT example can make this fail: 3 2 2 1 2 2 2 -1 2 -1 -2
But I have no test case to break the solution with the original constraints. I store the clauses increasing size and assign true to the first variable of the smallest clause, then erase its negation. I found a few more submissions using this approach (store clauses in a priority_queue instead), it would be nice if someone can prove this.
Actually it makes sense. In the view of the editorial's solution, this algorithm strips nodes with degree 1 first, until there are no such nodes. After that there are only cyclic parts left and then we can direct any edge in any direction. And repeat the algorithm
It removes the opposite occurences of the assigned variable from other clauses.
So after checking the first two clauses, there will be
(-3)^(3v1) -> assign -3 -> (1) -> assign 1 (it was already assigned but it's ok).
In the Minimisation Part-> I didn't understand from here: "There are no more than O(k2) states, and each transition can be made in O(1): we choose large or small group to add and obtain the number it adds to the sum by subtracting two elements of the sorted array"
Can someone please explain me the implementation of the Minimization problem with an example. Please. I am stuck for over a day now
For the problem Div1C, I think the statement “It is guaranteed that each variable occurs at most once in each clause.” is confusing. One may consider a variable can appear several times as long as it appears at most once in every clause.
I was not carefully reading the pre-statement "We know that each variable occurs in at most two clauses", but concentrating the last sentence, that'why I'm confused. Maybe the problem itself could be more clear.
I don't understand solution of problem div 2D/ div1B . I understand that there would be two groups, but how to prove that there will be (n mod k) and k — (n mod k) elements respectively and theirs sizes will be n/k and n/k + 1 ?
For problem 571D - Campus, my solution is constructing a tree for Military Offices and Universities and segment trees for queries. You can read my solution if you're interested.
Yeah, we had such solution, it's quite nice but we decided to publish another solution in the editorial, supposing it is less standard and easier to code.
Those who interested — can look at my solution.
Auto comment: topic has been updated by Kostroma (previous revision, new revision, compare).
Fortunately, I have found a way to publish links to submissions so that they are visible not only for admins of the round, thanks to PraveenDhinwa. Now you can look at author's solutions of our problems.
Nice. I didn't know about this trick and I participated virtually in my contest to publish solutions.
Does anyone know what method is used to solve CNF problem here?
I find this code much more comprehensible than the ones in the editorial and I'd like to see the big picture behind this code (the general theory). If all it represents is just the problem specific solution, then it's not as valuable as the editorial's solutions (because they allow me to practice the general widely used graph algorithms, like the matching algorithm), but I hope that there are some things to learn :)
Div2-A (Arrays) I had an hard time understanding the problem statement, it said that choose k (or m) numbers and if ANY of those numbers is lesser (strictly) than ANY of the number in array B.
Was that just me to think so?