Here's the first part of Hunger Games Editorial prepared by community. There are only my hints, see also the second blog, which will be soon published, with different, more detailed solutions written by many people :) I'd like to thank problemsetters team (PrinceOfPersia, keyvankhademi and aliasadiiii) for such wonderful contest. Hints will be probably updated when I'll learn more beautiful solutions for these problems :) Enjoy!
Problem A: Good Numbers
Suppose first integer is multiplied A times and second — B times. How many ways are there to complete the big number? Did we count something more than once?
Problem B: Hamro and array
Try to count numbers on even and odd positions separately.
Problem C: Hamro and Vampire Diaries
Suppose A[1] = x. How do we calculate A[1 + 3]? How to calculate next and all other values of A? What happens if n mod 3 = 0?
Problem D: Hamro and tools
Read about how STL can merge lists in O(1) or consider all queries in reverse order.
Problem E: LCM query
Suppose right end of our interval is i. How many different LCM's can we reach in the left? Many? Not many?
Problem F: Forfeit
What is the minimum weight of our tree such that it satisfies constraints? How does the sum change when we increase one edge by 1?
Problem G: Hamro and Icozup
//lel maths
Problem H: Hamro and Circles
//lel maths again, how to explain maths? :D Does this problem differ much from G? What should we change to get AC in H?
Problem I: Hamro and Khikhland's map
We will get the most cash if we take all adges except MST. Google MST if you don't know what it is :)
Problem J: Special Vertex
Suppose we've queried vertex X. Then, we get answer which subtree contains the special vertex, we can forget about all other subtrees of X and do this recurvisely on this subtree. How to choose X such that our solution becomes fast?
Problem K: Pepsi Cola <3
Let's count for each OR how many subsets have this OR. Try to think which OR-es affect which others. How to calculate it fast?
Problem L: It's not that bad (seriously, why does this task has such title?)
Go through all powers of 2 from largest to smallest (2^30 -> 1). For every visited power we'll try to build new graph. For every edge: if its value does not containthis power (value OR power != value) add it to the graph. Then, check if end is reachable from start. What if so? What if not?
Problem M: Guni!
Associate each Guni with maximum value in it? Do we have to maintain any other values in it?
Problem N: Demiurges play again
Try thinking in DP categories. Count dpmin[x] and dpmax[x] for each vertex. Suppose we've counted them for all subtrees of x, how to count them for x?
Problem O: Cheque
Do it "with induction" by K. Suppose we know minimum values for all vertices that are in the distance <= V from marked points. How to count them for V+1?
Problem P: Godzilla and Candies
Choose vertex x. Consider all queries in the graph. For each query only count those vertices which DO NOT belong to the same subtree of x. Then, extract x from graph and do it recursively on all sons of x subtrees. How to choose vertex x such that our solution becomes fast? (See also problem J).
Problem Q: Mina :X
Try to come up with DP which counts minimal number of questions for subset of size X. When we will enter X, we'll have already counted all possibilities, so consider all of them once more and see which of them we may check.
Problem R: Makegraph
Suppose we have answer 1 at some point. Do we already know all the future answers?
Problem S: Godzilla and Pretty XOR
Try to build S optimally. What will be maximal size of S? How to check whether we should insert new value or not?
Problem T: The ranking!
I still do not know how to solve it :( But look at sth cool instead ^^ https://piwoicydr.files.wordpress.com/2015/03/dsc_1126am.jpg
Problem U: Godzilla and chess
Will n^3/32 solution be efficient enough? How to write it easily?
Problem V: Godzilla and ugly XOR
Consider max and min values separately, let's build MIN. Start from the most significant bit. Do we have to add it now or we may later?
Problem W: Palindrome Query
We may use hashing for checking if two substrings are equal. For all updates it's easy to modify our hash. How to answer queries if there were no updates? Does something really change when they are?
Problem X: Tree Query
Use divide and conquer on tree, think in the same way as P. Choose vertex x, perform some queries, extract x from graph, do it recursively. How to choose x? (compare with P and J).











Auto comment: topic has been updated by kpw29 (previous revision, new revision, compare).
Feel free to ask questions, but I encourage you to think about solutions also :)
in problem Q, n=144 was a good hint for thinking about fibonacci :) Fibonacci search :D
Lol, I didn't notice that o.O Anyway it's usually easier for such tasks to come up with a DP rather than searching results greedily :)
I can write a solution for problem G (and H). Also problem B could be solved using partial sums.
It'd be very grateful if you could provide editorial in a written way, but source codes are also 'acceptable' :P
Well, it was awesome contest :) At first I was confused by three problems on centroid decomposition, but then I implemented it and it was very interesting. I would like to comment on some especially interesting problems:
Problem K: Pepsi Cola <3
Maybe this is the most beatiful math problem I have ever seen :) There is an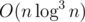 solution here. Let
solution here. Let 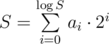 . Then
. Then 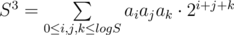 . If we needed only Pepsi number we could simply sum 2i·(amount of subsequences that contain at least one number with i-th bit). Well, we can do the same with triples of bits for Cola number! Here is my awesome solution with including-excluding formulae. #dLmckL
. If we needed only Pepsi number we could simply sum 2i·(amount of subsequences that contain at least one number with i-th bit). Well, we can do the same with triples of bits for Cola number! Here is my awesome solution with including-excluding formulae. #dLmckL
Problem W: Palindrome Query
Well, this is the second time I tried to solve this problem. And I think, this time implementation is especially simple. #8kLke7
Problem S: Godzilla and Pretty XOR
Also I was amazed by how short and simple solution for this problem was :) #0KF9Ra
About S: go kill urself XD I overkilled it with linear algebra and many observations, will update "big blog" soon with your solutions, thank you :)
But my solution contains linear algebra there. Just a simple implementation of it ;)
"go kill urself XD" — isn't it a little bit too forward just for having a clearer solution : D?