Cutting to the chase
Clearly you don't need a PhD in Computing to sweep in the yard , but one might be useful in order to know linear and radial sweep algorithms. So , what's all about ? It's just what it sounds it is , sweeping linear ( up to down , for example ) or radial ( making a 360 degrees loop ).
How this can help? Well...
Linear sweep
Suppose you a set of objects in an Euclidean plane. We need to extract information about some objects. The method of linear sweeping takes a line and moves it on a fixed direction. Usually the line taken would be vertical and the direction would be left to right or up to down.

Quite abstract for the moment , huh ? Let's go to a more specific example.
Rectangle union area
This example is well known. You have a set of rectangles with edges parallel to the OX and OY axes. What is their union area.
Well , first of all , let's take a particular case in order to achieve a different perspective. Let's suppose the lower edges are fixed on the OX axis. This would lead us to the following case :
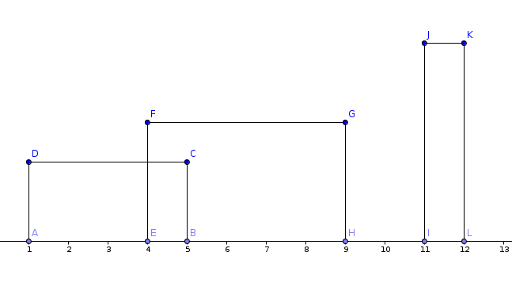
Now let's take a look at the property we established. The property fixes the lower edge. So the only edge we are interested in is the upper edge. The other two will be united by the point projections of the ends of the edge. For example D and C will be projected in B and A. Furthermore , these edges are useless in our problem so we will take into acount only the upper edges.
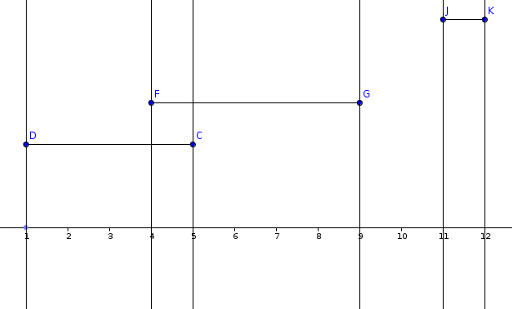
Now as we established that the sweep can go. We will "move" an imaginary line from left to right. As we meet a left corner of the segment we should take it into account for the moment. When we reach it's end it should not be considered any more. On a space between two sweep lines we take all the active segments and memorise the bigest Y. The area added would be maxY * length between sweep lines.
The only remaining question is how we move the imaginary line ? Sorting , of course.
Now let's summarise. We divide each segment in two types of queries : in ( a segment is active ) and out ( a segment becomes unactive ). Sort the queries increasingly by X coordinate and for each two consecutive sweep lines take the maximum Y out of the active sweep lines. We can easily do that with a priority queue. Therefore , the complexity would be O(N log N).
To be sure we understood all , let's look again at the example. The queries will be : in(D) , in(F) , out(C) , out(G) , in(J) , out(K). On interval DF' we have one active segment , therefore maxY = 2. On interval F'C we have two active segments , maxY = 3 from FG segment. On interval CG , maxY = 3 and finally on interval JK , maxY = 5. Total area is 3*2 + 1*3 + 4*3 + 1*5 = 26. Easy.
Now as we sorted that out, let's return to our original problem. Picture , yey: ( from TopCoder tutorial )
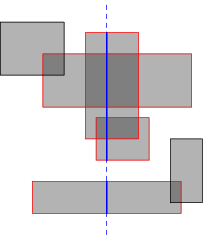
Now how to solve stuff like that if we have different Y coordinates for down edges. Well , we'll keep the principles stated above but use a different data structure : segment trees. First normalize all Y coordinates ( keep a vector with sorted Ys and work with the order in that sorted vector ). Now as we sweep on X coordinates we keep "in" queries for left edges and "out" queries for right edges.
Stop ! Segment tree time ! In a segment tree we keep all active (ny[idx],ny[idx+1]) ( where ny denotes the normalisation vector ) segments length sum ( in the picture there would be 6 such segments ) and add to the result the distance between sweep lines * above mentioned sum. As we go , we update the segment trees at in and out queries. Again complexity O(N log N).
Let's move on to ...
Radial sweep
Basically , it would go like that:

( Don't wait , it won't load ) So , what we have here ? A line with a fixed center rotating. The 360 and 180 rotations of lines and rays are commonly used. We will apply same principles to some problems.
Maximum number of points on a line
You are given a set of N points. Find the maximum number of points on a line. For the example line AB , answer 5.
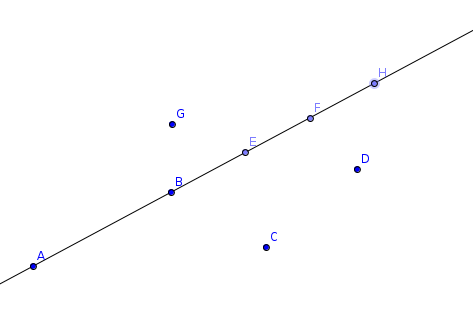
What should we start with ? Bruteforce. Let's consider we fixed a line and we want to know how many points of the N are on it. Make the equation and verify. The complexity would be O(N^3) cause we'll fix O(N^2) lines. What's slow at that ? We try the same line more times and furthermore we try all the points and that's slow.
Let's fix a point from the line. Now the line should rotate around this point , like in the picture below.
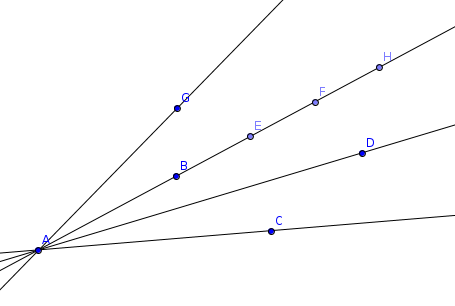
Here comes the sweep. Radial sweep. For simplicity as we fixed a point as the "center" move it to the origins along with all the other points. Now sort the points trigonometrically. ( or clockwise if you want ) Put the angles in an array. Now go through the array and count the number of points with same angle and that's it.
For the example we have point B C D E F G H. After sorting we have G B E F H D C and the angles will be the same for the sequence B E F H. So answer will be 5.
You may be asking yourself why the hack is the solution correct cause if we take B as the center we will count only 4 points. It is guaranteed that if the rightmost point from the right is taken as a center all the points on the right will be found.
Note: We could have used hashes ( that's a better complexity ) or maps ( same ) , but we insisted only on the sweep approach.
Don't mess with the circles
Given a set of N points on a plane , determine the circle of a fixed radius R which covers the most points in S.
Now this is more tricky. Remember Shrinking Trick ? Draw a circle from each point and find out a point that is in the most circles. Let me help you with this , look :
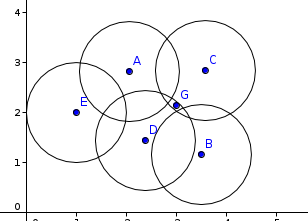
In the given example the set is A,B,C,D,E. Now , as an example , point G would be would cover 2 points in the set. ( D and C ). The maximum number of points that can be covered would be 3.( for example at intersection of discs B,C and D ) Another useful observation is that a point in solution can be found at the intersection of at least two circles. How many intersections there are ? O(N^2). This makes an O(N^3) solution by testing any possible center with respect to all the points.
Now how we sweep this off ? Before choosing a fixed point was good , so we fix some circle. We see how it's corresponding disk interacts with other discs , so we can choose an interval that would give all the points that can be a solution for both circles. That is O(N) for each circle and we settled some intervals.
Now the problem goes as follows : given some intervals on a circle how to find a point where the intersection is maximal. We will treat them as segments. So sort them clockwise , then process them. I leave this to the reader as we do it similarly to the in-out segment procession described above. Finally , the complexity would be O(N^2 log N).
Bonus
PS:
Please state your opinion on my tutorial. Also , if you have any suggestions on what the next tutorial should be on , feel free to comment. Hope you enjoyed.
EDIT: Thank you for all your support. This surely convinced me to write more articles in the future.
EDIT2: Few more problem at caioaao's suggestion:











Auto comment: topic has been updated by DanAlex (previous revision, new revision, compare).
Auto comment: topic has been updated by DanAlex (previous revision, new revision, compare).
"Gif" image doesn't work :\
Will fix that when I have more time. Thanks.
LE : Could not find a working one. If someone can , please PM me.
Auto comment: topic has been updated by DanAlex (previous revision, new revision, compare).
Auto comment: topic has been updated by DanAlex (previous revision, new revision, compare).
Very nice tutorial! It would be great if you could do some more topics on Geometry!
Thanks for the article , can we use sweep to find the area of union of N circles not necessarily of the same radius? N<=2000
I do not exactly know how to implement , but I think that thinking of the area as a difference of 2 integrals would do.
More specifically we need to find the difference between the upper and lower envelope of each cluster of circles. To do that observe that there are only O(N×N) points of interest (leftmost point of a circle , rightmost point of a circle and circle intersection points ). In other words we simply divide each circle in 4 functions and there are just some specific points when a function can surpass another.
Therefore the complexity should be O(N×N log N) due to necessity of sorting.
I think integral approach to solve circles union problem is very simple.
there is no need to record leftmost point and rightmost point of a circle.we only focus on arg segments that is outside(not covered by other circles) and sum up all these outside arg segments' intergal value
double fun(int id,double x)
{ return cir[id].r*cir[id].y*cos(x)-0.5*cir[id].r*cir[id].r*x+0.25*cir[id].r*cir[id].r*sin(2*x);
}
answer+=fun(id,lt)-fun(id,rt) lt is left point of segment,rt is the right point of segment.
sorting of pole arg is counterclock wise but compute the integeral is clockwise,and fun()is the original function,so fun(id,lt) minus fun(id,rt) is correct
you can try this harder problem:
http://codeforces.com/gym/100443
J cleaning the hallway..
integral is a good approach to solve this problem...
I am also curious about a simpler approach or solving with better complexity.
I have sketched an idea as to how I would approach this problem. I don't know if it is feasible, but it might work.
Here's an example:
The main idea is:
0) Do not take into account circles that are inside other circles -> they are irrelevant to the answer.
1) For each circle, find out the arcs that share common space with other circles. This should be a reunion of disjoint segments. (note now that the arcs that do NOT share any space with the circles are also segments
2) Calculate the area of the polygons that describe the common regions (yes, they are always polygons) (hashed area)
3) Calculate the regions that are unique for each circle (hashed area)
Steps 1) and 3) should be easy enough. What concerns me now is step 2), which seems to require a lot of attention, not to mention the fact that the segments I am talking about are very tidious to implement, given the "finite field" nature of the angles (they loop around at 2*PI)
Edit: I am pretty sure that, in the "intersection graph", each polygon would represent a clique of the graph.
Really nice editorial. I was just looking for something like that. But I would like to make some remarks
Why would we count 4 points, if we pick B as a center? There are definitely 5 points on that line, aren't there? Maybe the problem is that you sort points by the angle in range (-pi, pi] and it corresponds to sorting points by rays, not by lines. The angle between the line and x axis lies in range [0,pi) or (-pi/2, pi/2] whatever you like more. This doesn't affect the result at all, it is just not a reason to complain about solution not working properly, since you actually implemented the different one :)
Do you know some special segment tree, which will be able to get the necessary sum for "Rectangle union area"? I only know about a segment tree which can calculate exactly the opposite thing, i.e. the length of segments, that are not covered by any rectangle on the line.
I couldn't understand what kind of problem is being solved in "Don't mess with the circles". The part "determine the minimum radius circle of a fixed radius R" is really hard to understand. I suppose the "minimum radius" is not meant to be there :)
What do you mean by "special segment tree"? If you know about a segment tree that will calculate which segments are not covered, will not just reversing how you code this segment tree get you the answer you want directly?
You're right about the last point, the statement should be simply "determine the circle of a fixed radius R which covers the most points in S".
While we're English nitpicking, "abordation" is not an English word. Speaking a latin language, I know exactly where you're coming from, though. The word you want is "approach".
It's probably from the way I explained the part with the 4 points. Suppose you have angles indexed from [0,360) and we count from ray [BE ( denote BE at 0 degrees ) , that would be points B,E,F,H and separate for 180 degrees we will have points B,A.
"the length of segments, that are not covered by any rectangle on the line" is ok. Substract this from "total".
Uf , lots of typos , thanks a lot mate. :D I thought initially explaining something else but then changed my mind. Yes , minimum radius is not supposed to be there. I will try to make clear explanations tomorrow.
ffao , yeah , you're right about "approach". :))
I know how to solve the rectangle union area. I think I even solved it once :).
I was just curious if we can calculate the length of segment's union directly. At least I got the impression that it was a proposed solution after reading the explanation. Maybe I misread it somehow....
Yes, we can !!!
Let's keep a segment tree as:-
in(segment)---> update (ny[y1],ny[y2]]) with 1
out(segment)---> update (ny[y1],ny[y2]]) with -1
segments length sum---> query (whole range) for no. of non-zero elements.
But wouldn't your segment tree be of size O((max_y — min_y) * log (max_y — min_y)) which is independent of N? If I'm not mistaken we want this tree to be O(N log N) in size. I'm just asking, I'm not sure how to implement this in "rectangle area union".
I'm no expert at segment trees. Anybody knows a good article how can we implement them?
Anyway, really great tutorial! Sweeping was always a bit tricky for me, maybe now I will be able to start solving problems regarding this topic.
Have you ever heard about coordinate compression? This can solve the segment tree size problem, you should look it up.
Ok, now I see how to implement it. Thank you very much!
My point was that, depending on how you code your segment tree, just reversing the zeros and ones (a full leaf is 1, an empty leaf is 0) should reverse the value the segment tree computes.
I would have to know exactly how you code your segment tree, but keeping "count of rectangles that cover this interval completely" and "sum of squares in this interval that are covered" does the trick.
I used different tree. It could perform three operations: add V to segment, get minimal value and count its frequency. As you can see, reversing values just wouldn't do the trick.
Anyway, it is always nice to know different approach :).
Nice post!
I don't get the last problem. First, I see G covers only only 2 points, C and D. (not 4). Second, I don't see how to check how many points does an intersection of two circles cover. E.g. if we first take C and D and we consider their intersection, we can try to add A or B but not both, because the intersection zone changes. The problem is that we have zone, not a single dot.
What is meant by "intersection of two circles" are the two intersection points of the circle lines.
So in your case, if we start with circles C and D, one of the intersection points lies inside circles A,C,D and the other inside B,C,D.
The first observation is valid and I messed up the example. Sorry for that and thank you.
I haven't understand about point G too. It seems to be covered only by two points, not four. Everything else is clear, the way editorials should be done.
Yes, there is a corner case in the same place: several circles with the same center. We should also check all the centers (O(n) more points). But it doesn't change the main idea.)
I updated it now , should be clear :)
One becomes a Sir of sweep line when he has managed to implement and got accepted Fortune's algorithm ...
... during the contest :)
Heh, and did you? ;)
I remember, several years ago I was writing a contest with my team. Only one hour left, and one problem. I glanced at it and said: "Guys, this is a Delaunay triangulation, I'm pretty sure I can implement it in an hour!" I never ever was that wrong. Later it took me about two evenings to make it, and I doubt I'd ever attempt writing it during the contest once again.
No, because it is strictly prohibited to participate in the contest if you are its problemsetter.
we can use sweep line for finding intersection points between line segments ( everyone knows :D ) but can someone tell me how we should handle the case when some segments have same point in one of their end points ? or in a case when intersection point lies on some segments end points ? example : segment A ( x1 = 0 , y1 = 0 , x2 = 3 , y2 = 3 ) , segment B ( x1 = 0 , y1 = 0 , x2 = -3 , y2 = -3 ) , segment C ( x1 = 3 , y1 = 3 , x2 = 6 , y2 = 0 ) , segment D ( x1 = -3 , y1 = -3 , x2 = 6 , y2 = 0 ) , segment E ( x1 = -3 , y1 = -3 , x2 = 3 , y2 = 3 ) ,
Auto comment: topic has been updated by DanAlex (previous revision, new revision, compare).
In problem "Maximum number of points on a line" we can fix point (a,b) and normalize other points (x, y) as (1, (y-b)/(x-a)), so we must insert in map (y-a)/(x-a) or insert in vector and sort. For better complexity we must not insert points where x < a
How did you choose A in the radial sweep?
We fix each point as a center, therefore the
O(N^2 log N)complexity.Nice tutorial. I think it'd be useful if the sorting stuff were be more detailed (specially the radial sort). For me, it's the most challenging part of the sweep-related problems.
Some related problems you could append to the post:
Linesweep and line segment sorting: https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=4376
Radial sweep and line segment sorting: https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=4413
PS: Although our group didn't work out as planned, I'm glad to see you passed the "purple barrier" :D congrats
Thanks a lot mate. For sorting you can always use STL ( for example look here ). I will add the problems. Also we can renew the group any time if we have enough useful ideas for managing it in a better way. ;)
STL is not always the solution, for example: something like radial sort would require some extra care. If you sort it using angles, everything is fine, but you may bump into a lot of precision issues. The best, when precision is an issue, is to use the cross-product between two points to determine their ordering, but that alone is not a valid sort as you can have A < B < C < A. What I do is to sort first by the points' quadrants to eliminate this property and only then check the cross product.
It depends on what you are trying to implement. Using the cross product is actually the same as comparing the slopes , so if you want to move with a ray you should also keep a sign for upper or lower quadrants.
Can someone provide me an implementation of the idea of rectangle union? I am trying to understand it but I ain't good enough.
here is the answer: https://codeforces.com/blog/entry/44484?#comment-290099
it's just a lazy segment tree.
Is there any online judge to test my code for 'Maximum number of points on a line' and 'Don't mess with the circles'?