I am very much trying to understand iterative dp but not getting it comfortable. I've done many paperwork. For example: For the following problem I can design a solution which run on O(n*k*S) which is not efficient. Can you help me on this that how to understand, find out solution in iterative dp? I can design recursive dp bt can't transform it in iterative dp.
Problem: LightOj-1145
You have N dices; each of them has K faces numbered from 1 to K. Now you have arranged the N dices in a line. You can rotate/flip any dice if you want. How many ways you can set the top faces such that the summation of all the top faces equals S?
Now you are given N, K, S; you have to calculate the total number of ways. Input
Input starts with an integer T (≤ 25), denoting the number of test cases.
Each case contains three integers: N (1 ≤ N ≤ 1000), K (1 ≤ K ≤ 1000) and S (0 ≤ S ≤ 15000). Output
For each case print the case number and the result modulo 100000007.
Sample Input:
5
1 6 3
2 9 8
500 6 1000
800 800 10000
2 100 10
Sample Output:
Case 1: 1
Case 2: 7
Case 3: 57286574
Case 4: 72413502
Case 5: 9










Will O(T * N * S) pass?
If so you can calculate
dp[i][s]in O(1). Your O(N * S * K * T) solution does this in O(K). When have:dp[i][s] = sum(dp[i - 1][s - j]) for each j = [1; k]so your solution just iterates all j. The key part is to reduce this cycle to O(1). We can do this with partial sums.
If we have partial sums by S how can we find
sum(dp[i - 1][s - j]) for each j = [1; k]?It's easy:
pref[i - 1][s] - pref[i - 1][s - k - 1].Now we just need to find how to calculate the partial sums. We can simply after completing all
dp[i][s]we iterate overdp[i]andpref[i][s] = pref[i][s - 1] + dp[i][s].So I think this will be a valid solution.
can you explain me how can i solve this problem by using only two row?
The logic is, when you start computing the value for ith row compute a prefix sum array for the previous that is the (i-1)th row and using that you can compute the values of each index in the ith row in O(1). So the complexity reduces to size of the DP Array for each test case. So the total complexity becomes O(T*N*S).
I guess you mean 2 dimensions ?
Let dp[i][j] be the number of ways you can make a sum of j using the first i coins.
Assume you want to fill dp[i][j] at the moment. Note that :
dp[i][j] will be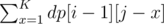 . Why ?
. Why ?
When you add some dp[i - 1][j - x], means that you are currently using the face of current die having value x, as j - x + x = j. As you can use all faces from 1 to K, it becomes prefix sum of all those values, that is looked up in O(1).
The answer will be in dp[n][S]
yes, note that you only ever need rows i and i — 1, therefore, you can discard every row prior to that, and use only two rows.