Let's discuss problems.
How to solve E and F.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 7 | SecondThread | 150 |
| 9 | pajenegod | 145 |
| 9 | orz | 145 |
Let's discuss problems.
How to solve E and F.
| Name |
|---|



Auto comment: topic has been translated by Temirulan (original revision, translated revision, compare)
E — sort edges in descending order. Then add edges one by one keeping number of:
Then numv = v - v0 - v2 + cycle
and nume = eadded - v2 + cycle.
What about 10^5 queries?
Sort them and answer query in time when graph is in conditions described by it.
How to solve div.2 B — "B. Book Borders", I've got TLE. And div.2. D — "D. Digit Division"?
My solution is Log(b — a) * (b — a) * Log(w). I iterate from a to b foreach i finding how many words would be on each next string of length i. This is O((b — a) / i * f(i)), where f(i) is the complexity of "finding how many words would be on each next string of length i".
f(i) can be doen with binsearch: lets assume we've already proceded L words, so now we have to find maximum of such R that lengths of words from [L + 1, R] + R — L(count space characters) is <= i. Well, calculate prefix sums for words' length, then find R simply with binsearch. Dont forget to add length of L + 1 word to your answer(thats what we have to do :) )
Why is this (b — a) * Log(b — a) * log(w)? Log(w) goes for binsearch obviously; for some reason Sum(i / n, {i from 1 to n}) is Log(n) / n, so when we iterate for each i in [a, b] we do O(b — a) * Log(b — a) operations. Idk why it passes time limit, it looks like ~1.8 * 10^8, but it does. That's it
Here are the slides from the solution presentation held onsite: https://goo.gl/6IFvGQ
They don't describe solutions in great depths, but hopefully you can get some hints from the slides.
Problem div.2 'A. ASCII Addition' in russian differed from english that it had a screenshot of ASCII art instead of text in pdf (which is copied very comfortable as chunks of 7 x 5 lines) and it could save some minutes of coding. (Besides scripting languages here were helpful http://ideone.com/7Hz8qP )
Or u could just copy it from input
You coudn't fast-copy chunks of 7 x 5 from input, you copy whole 7 lines.
w/e
It seems that there are some problems with standings. My team solved 4 tasks during contest, but in official standings we have 7.
UPD. Fixed.
It's not a bug, it's a feature =)
Could someone please share code for problem I that passed without additional optimizations?
Our solution is O(max_coordinates) per one query and doesn't use sqrt (only arithmetic operations with doubles), but gets TL 11 and I have no idea what to do with it :(
Here's our code (author is meshanya). It passed with 2x gap, even though it is Java. Actual solution is in method solve() (as it is always the case with CHelper's code).
It requires @google.com account :/
Oh shi~, wrong pastebin :( Updated the link. (I would also be grateful to CF admins if they remove the previous revision of the comment)
Thanks a lot. Now we have something to compare and can find out why our code is so slow.
Could someone please outline the alternative solution to problem F, which doesn't involve Karatsuba or FFT.
There is one solution that passes the tests but is wrong:
find k = c / (a+b-1)
let G(i, j) = F(i, j) + k
now G(i, j) = aG(i, j-1) + bG(i-1,j)
find G(n, n) and use F(n, n) = G(n, n) — k to obtain final solution.
solution fails on case where a+b-1 = 0 (mod 10^6+3)
Thanks. Btw, when can we expect to see the problemset and test data? I'm looking forward to solving them.
There are also solutions that work ;). To recollect, main problem is to compute sum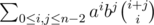 . Let S(k) be sum of all summands such that i + j = k. We can note that it is almost true that S(k) = (a + b)S(k - 1). It is true for k ≤ n - 2, however for k > n - 2 you need to subtract two terms, which can be done in constant time (possibly after some precomputations of factorials etc.). Key argument here is of course
. Let S(k) be sum of all summands such that i + j = k. We can note that it is almost true that S(k) = (a + b)S(k - 1). It is true for k ≤ n - 2, however for k > n - 2 you need to subtract two terms, which can be done in constant time (possibly after some precomputations of factorials etc.). Key argument here is of course 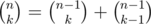
Explain please Div2 L(Larry’s Lemma)
How to solve J?