606A - Magic Spheres. Let’s count how many spheres of each type are lacking to the goal. We must do at least that many transformations. Let’s count how many spheres of each type are extra relative to the goal. Each two extra spheres give us an opportunity to do one transformation. So to find out how many transformations can be done from the given type of spheres, one must look how many extra spheres there are, divide this number by 2 and round down. Let’s sum all the opportunities of transformations from each type of spheres and all the lacks. If there are at least that many opportunities of transformations as the lacks, the answer is positive. Otherwise, it’s negative.
606B - Testing Robots. Let’s prepare a matrix, where for each cell we will hold, at which moment the robot visits it for the first time while moving through its route. To find these values, let’s follow all the route. Each time we move to a cell we never visited before, we must save to the corresponding matrix’ cell, how many actions are done now. Let’s prepare an array of counters, in which for each possible number of actions we will hold how many variants there were, when robot explodes after this number of actions.
Now let’s iterate through all possible cells where mine could be placed. For each cell, if it wasn’t visited by robot, add one variant of N actions, where N is the total length of the route. If it was, add one variant of that many actions as written in this cell (the moment of time when it was visited first). Look, if there is a mine in this cell, robot would explode just after first visiting it.
The array of counters is now the answer to the problem.
605A - Sorting Railway Cars. Let’s suppose we removed from the array all that elements we would move. What remains? The sequence of the numbers in a row: a, a+1, …, b. The length of this sequence must be maximal to minimize the number of elements to move. Consider the array pos, where pos[p[i]] = i. Look at it’s subsegment pos[a], pos[a+1], …, pos[b]. This sequence must be increasing and its length as mentioned above must be maximal.
So we must find the longest subsegment of pos, where pos[a], pos[a+1], …, pos[b] is increasing.
605B - Lazy Student. Let’s order edges of ascending length, in case of a tie placing earlier edges we were asked to include to MST. Let’s start adding them to the graph in this order. If we asked to include the current edge to MST, use this edge to llink 1st vertex with the least currently isolated vertex. If we asked NOT to include the current edge to MST, use this edge to link some vertices that are already linked but have no edges between them. To do this it’s convenient to have two pointer on vertices (let’s call them FROM and TO). At the beginning, FROM=2, TO=3. When we are to link two already linked vertices, we add new edge (FROM, TO) and increment FROM. If FROM becomes equal to TO, we can assume we already added all possible edges to TO, so we increment TO and set FROM to 2. This means from this moment we will use non-MST edges to connect TO with all previous vertices starting from 2. If it appears that TO looks at currently isolated vertex, we can assume there are no place for non-MST edge it the graph, so the answer is Impossible. Keep doing in the described way, we’ll be adding MST edges as (1,2), …, (1,n) and non-MST edges as (2,3), (2,4), (3,4), (2,5), (3,5), (4,5), ...
605C - Freelancer's Dreams. We can let our hero not to receive money or experience for some projects. This new opportunity does not change the answer. Consider the hero spent time T to achieve his dream. On each project he spent some part of this time (possibly zero). So the average speed of making money and experience was linear combination of speeds on all these projects, weighted by parts of time spent for each of the projects.
Let’s build the set P on the plane of points (x, y) such that we can receive x money and y experience per time unit. Place points (a[i], b[i]) on the plane. Add also two points (max(a[i]), 0) and (0, max(b[i])). All these points for sure are included to P. Find their convex hull. After that, any point inside or at the border of the convex hull would correspond to usage of some linear combination of projects.
Now we should select some point which hero should use as the average speed of receiving money and experience during all time of achieving his dream. This point should be non-strictly inside the convex hull. The dream is realized if we get to point (A,B). The problem lets us to get upper of righter, but to do so is not easier than to get to the (A,B) itself. So let’s direct a ray from (0,0) to (A,B) and find the latest moment when this ray was inside our convex hull. This point would correspond to the largest available speed of receiving resources in the direction of point (A,B). Coordinates of this point are speed of getting resources.
To find the point, we have to intersect the ray and the convex hull.
605D - Board Game. Consider n vectors starting at points (a[i], b[i]) and ending at points (c[i], d[i]). Run BFS. On each of its stages we must able to perform such an operation: get set of vectors starting inside rectangle 0 <= x <= c[i], 0 <= y <= d[i] and never consider these vectors again. It can be managed like this. Compress x-coordinates. For each x we’ll hold the list of vectors which first coordinate is x. Create a segment tree with first coordinate as index and second coordinate as value. The segment tree must be able to find index of minimum for segment and to set value at point. Now consider we have to find all the vectors with first coordinate from 0 to x and second coordinate from 0 to y. Let’s find index of minimum in the segment tree for segment [0, x]. This minimum points us to the vector (x,y), whose x — that index of minimum and y — value of minimum. Remove it from list of vectors (adding also to the queue of the BFS) and set in the segment tree to this index second coordinate of the next vector with first coordinate x. Continue this way while minimum on a segment remains less than y. So, on each step we will find list of not yet visited vectors in the bottom right rectangle, and each vector would be considered only once, after what it would be deleted from data structures.
605E - Intergalaxy Trips. The vertex is the better, the less is the expected number of moves from it to reach finish. The overall strategy is: if it is possible to move to vertex better than current, you should move to it, otherwise stay in place. Just like in Dijkstra, we will keep estimates of answer for each vertex, and fix these estimates as the final answer for all vertices one by one, starting from best vertices to the worst. On the first step we will fix vertex N (the answer for it is zero). On the second step – vertex from which it’s easiest to reach N. On the third step – vertex from which it’s easiest to finish, moving to vertices determined on first two steps. And so on. On each step we find such vertex which gives best expected number of moves if we are to move from it to vertices better than it and then we fix this expected number – it cannot change from now. For each non-fixed yet vertex we can find an estimate of expected time it takes to reach finish from it. In this estimate we take into account knowledge about vertices we know answer for. We iterate through vertices in order of non-increasing answer for them, so the answer for vertex being estimated is not better than for vertices we already iterate through. Let’s see the expression for expected time of getting to finish from vertex x, considering use of tactic “move to best of i accessible vertices we know answer for, or stay in place”:
m(x) = p(x, v[0]) * ans(v[0]) + (1 — p(x, v[0]) * p(x, v[1]) * ans(v[1]) + (1 — p(x, v[0]) * (1 — p(x, v[1]) * p(x, v[2]) * ans(v[2]) + … + (1 — p(x, v[0]) * (1 — p(x, v[1]) * … * (1 — p(x, v[i-1]) * m(x) + 1
Here m(x) – estimate for vertex x, p(a,b) – the probability of existence of edge (a,b), and ans(v) – known answer for vertex v.
Note that m(x) expressed by itself, because there is a probability of staying in place.
We will keep estimating expression for each vertex in the form of m(x) = A[x] * m(x) + B[x].
For each vertex we will keep A[x] and B[x]. This would mean that with some probabilites it would be possible to move to some better vertex, and this opportunity gives contribution to expected time equal to B[x], and also with some probability we have to stay in place, and this probability is A[x] (this is just the same as coefficient before m(x) in the expression).
So, on each step we select one currently non-fixed vertex v with minimal estimate, then fix it and do relaxation from it, refreshing estimates for other vertices. When we refresh estimate for some vertex x, we change its A[x] and B[x]. A[x] is reduced by A[x] * p(x,v), because the probability of staying still consider it’s not possible to move to v. B[x] is increased by A[x] * p(x,v) * ans(v), where A[x] is the probability that it’s not possible to use some vertex better than v, A[x] * p(x,v) is the probability that it’s also possible to use vertex v, and ans(v) – known answer we just fixed for vertex v. To calculate the value of estimate for some vertex x, we can use expression m(x) = A[x] * m(x) + B[x] and express m(x) from it. Exactly m(x) is that value we should keep on the priority queue in out Dijkstra analogue, and exactly m(x) is the value to fix as the final answer for vertex x, when this vertex is announced as vertex with minimal estimate at the start of a step.










My solution to C: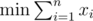 subject to
subject to 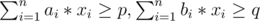 . The dual of this problem is max p * y1 + q * y2 subject to ai * y1 + bi * y2 ≤ 1. It's convex, so we can use a simple ternary search.
. The dual of this problem is max p * y1 + q * y2 subject to ai * y1 + bi * y2 ≤ 1. It's convex, so we can use a simple ternary search.
wow it's Too Simple!
TooSimple*
your joke is too outdated now :D
I actually find it Too Difficult now :)
Could you explain how do you get dual of the problem, please?
http://web.mit.edu/15.053/www/AMP-Chapter-04.pdf
You can check this lecture. Duality in linear programming is very important in combinatorial optimization problems like graph matching and many approximation algorithms.
Although simplex works in time O(C(n + m, m)) it passed system tests.
Not Too Simple, it is Too Simplex
Not TooSimple but truly subtle!!
I'm not able to understand why the function is convex. Can someone please explain?
Can anyone please tell me the complexity of Simplex Method to solve Linear Programming problems? I used that method to solve C, but I do not know its complexity.
Why does the second test case of Div. 2 problem D (Div. 1 problem B) return -1?
IN:
3 3
1 0
2 1
3 1
OUT: -1
Thanks
The graph consists of three vertices and three edges — there is an edge between each pair of vertices. For the MST we need to pick two of the edges so that their sum is minimum — therefore we pick the edges with weights 1 and 2. However, Vladislav didn't include the edge with weight 1 in his MST.
But why this test case does not return -1? A edge with weight 3 is not chosen, but a one with 4 is. Shouldn't we choose the one with 3?
IN:
4 4
2 1
3 0
3 1
4 1
OUT:
1 2
2 3
1 3
1 4
If we look at the graph that the output creates, we can see that the only way that we can reach vertex 4 is by using the edge between vertices 1 and 4. There's no spanning tree on the graph that does not include the vertex with weight 4.
Isn't the following graph valid as an output for this example (supposing we take vertex with weight 3 instead the one with 4)?
1 2
2 3
3 4
1 3
Yes.
The task was to reconstruct one of the graphs that match Vladislav's description. There are multiple different answers for sample 1. However for sample 2 no graph matches the description.
This is due to the Minimum-Cost Edge property of a MST.
If the edge of a graph with the minimum cost e is unique, then this edge is included in any MST.
Proof: if e was not included in the MST, removing any of the (larger cost) edges in the cycle formed after adding e to the MST, would yield a spanning tree of smaller weight.
In the given graph, 1 is the minimum cost edge but it is not included in the MST, hence no graph is possible.
Source: Wikipedia
But why this test case does not return -1? A edge with weight 3 is not chosen, but a one with 4 is. Shouldn't we choose the one with 3?
IN:
4 4
2 1
3 0
3 1
4 1
OUT:
1 2
2 3
1 3
1 4
I really liked Div1 B, very original and different problem. The ones where you reconstruct a graph from some information are always interesting.
During the contest I (mis)read Div2A as requiring that I turn (a,b,c) into exactly (x,y,z). Out of curiosity does anybody know how to solve that problem?
Oh facepalm I read it as this too. No wonder I couldn't solve it during the contest :/
Because of this, I thought about it for a long time near the beginning--found out that you could get (-1 -1 -1) in 3 steps, (-1 -1 0) and permutations in 2 steps. But you can't get (-1 0 0) in 1 step, and therefore can't get (x-1 y z) within (-x — y — z + 1) steps. Couldn't figure out much more, so moved on to other problems.
Я правильно понимаю, что в С размер выпуклой оболочки худшего теста несколько меньше n и есть величина порядка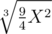 , где X = 106 ограничение на каждую координату?
, где X = 106 ограничение на каждую координату?
The solution for 606A Magic Spheres presented here is trivial, but is it really correct?
I spent almost an hour during the contest figuring out how to balance the amount of rocks in each pile so that the final distribution is exactly equal to the final requirements.
For example, what if a=b=c=1 and x=y=z=0??? In that case it would be impossible to reach this final distribution, even though your simplistic solution gives a positive answer.
Can someone explain why the author's solution is NOT wrong? Or is the problem formulation incorrect?
"To make a spell that has never been seen before, he needs at least x blue, y violet and z orange spheres."
Damn it...
Charlie Foxtrot.
I added edges in a different manner. all the mst edges were added as (1,2) , (2,3) , (3,4).. and then non — mst edges were added as (1 3) ( 1 4 ) ... (1,n) (2 4)...(2,n)....... Why is this wrong?
I did the same thing. Can't figure why this is wrong
Say, by your method the edges added were of weight 2 between 1,2 and 2,3 and weight 3 between 1,3. Let all other edges be in the MST.
This does not give the correct spanning tree for the graph.
I’m not sure I follow. What’s the input and what’s the graph?
Making the MST edges (1, 2), (2, 3), (3, 4), (4, 5), ... isn’t wrong, and my solution doing that got accepted.
Make sure you increment the larger index only when you run out of the smaller index’s range, not the other way round: (1, 3), (1, 4), (2, 4), (1, 5), (2, 5), (3, 5), (1, 6), ... If you try to increment the larger index first, you’ll find that for some k you’ll try to add edge (1, k) before you add edge (k - 1, k), so you’ll skip it and go back to (2, 4), and eventually you’ll run out of space to add new edges and incorrectly conclude that the corresponding graph can’t exist.
Also make sure to look at edges that are within the MST before edges that are outside it but have the same cost.
D is also could be solved with divide-and-conquer. The first step is to reduce problem to 0-1 bfs (we can always decrease our skills for free and can cast one spell to change the skills from (a,b) to (c,d)). If we add all edges there will be O(n2) 0-edges, but it's possible to add additional vertices in such way that we will only need
additional vertices in such way that we will only need  0-edges and path in our new graph will correspond to path in old graph with same length.
0-edges and path in our new graph will correspond to path in old graph with same length.
So, how to add new vertices in that way? Let's separate all initial vertices into two halves such that all vertices in the first half is on the left from vertices in the second path. There will be vertical line divides all vertices in that way. Denote it's x-coordinate as x0. We have to add vertices with coordinates (x0, y0), (x0, y1), ..., (x0, yk) where y0, ..., yk are all y-coordinates of the whole set of vertices. (y0 < y1 < ... < yk). For the vertex (x, y) such that x ≤ x0 we should add edge from (x0, y) and if x ≥ x0 it would be edge from (x, y) to (x0, y). Also we should add edges from (x0, yi) to (x0, yi - 1) for every possible i.
That's it, then we should find shortest path in that 0-1 graph.
The simple search maximum increasing subsequence in problem C. And answer in n-maxsub
14742819
Can someone plz explain me Div2 C in easy language and why we are making pos array as mentioned in the editorial.
PLZZZZZZZ.
We are looking for the largest possible set of numbers that we will not touch during the sorting (longest increasing subsequence), every other element is going to be moved either to the front or to the back.
If two numbers, lets say 4 and 5, are part of such set, 5 must occur after 4. The fastest way to check this is if we have stored the location of 4 and 5 in pos, so that we can simply check whether ( pos[4] < pos[5] ) is true.
By iterating through the pos array we can easily find the longest segment where the equation holds for each pair of consecutive elements.
Can you please explain how we are finding Longest Increasing Subsequence in Linear time?
This is a special case since the N elements are numbered from 1 to N. For example, sorting such an array requires a linear amount of work since we can simply assign every element to the position indicated by their number.
In this task, we can find the longest increasing subsequence by checking the cars from 1 to N in a single loop. The standard LIS algorithm involves binary searching, but our pos array replaces the O(logN) searching with O(1) array lookups. Such an array could not be constructed if the element values were not bounded by N.
It is not longest increasing subsequence. It is longest increasing subsequence WHERE EACH PAIR OF ADJACENT ELEMENTS DIFFER BY 1.
I am confused :/ Is it longest increasing subsegment (as written in editorial) or longest increasing subsequence? Or it is longest increasing subsequence WHERE EACH PAIR OF ADJACENT ELEMENTS DIFFER BY 1 .. ?!
It depends on the array (input / pos)
couldn't get till now :( maybe I should try something else and then try this again..
actually we have to find "**lics**"-> longest increasing consecutive subsequence
i dont get it in test 21:
7
1 3 5 7 2 4 6
the lics(longest increasing consecutive subsequence):
will be 1 3 5 7
but the answer is 5 what am i doing wrong here ?
Got it thankyou
In Div2D,shouldn't tie breaker be the other way round? Placing the edges included in the MST earlier?
Yes, I think so. I got accepted with the tie breaker you said, and placing earlier edges that we were asked not to include in the MST would fail (using the algorithm described) in cases like this:
3 3 1 0 1 1 1 1
I think x)
Thank you. Sure the tie breaker should place MST-edges first. It was mistake on translation. Fixed.
In div1 C why do we need to add points (max(a[i]), 0) and (0, max(b[i])) to our set of points? If I'm not wrong, is this done to ensure that our ray definitely intersect with our convex hull?
yes
I don't know but seems I can't understand test 8 in problem Div2A: 2 2 1 1 1 2 Jury's Answer is No. But simply we transform one blue and one violet into one orange and we get 1 1 2 Which is required, so why is the answer no? Can anyone explain?
Ah I got it, we most transform two of the same color, now I get it
Can anyone explain the solution to Div-1 C given in the editorial a bit more? Why is the given problem solvable using Convex Hull and the intuition behind it?
Think of the distinct projects as vectors pi = (ai, bi). On time t you can reach any of the points t·pi, but you can also reach any convex combination of them. The points that can be obtained as a convex combination of a certain set of points is the convex hull of that set.
If you take into account that, whenever is possible to reach (x, y) you can also reach any (x', y') such that 0 ≤ x' ≤ x and 0 ≤ y' ≤ y (that is the rectangle with corners in (0, 0) and (x, y)). You also need to add (0, 0), (0, maxy) and (maxx, 0) to the set {t·pi}1 ≤ i ≤ n. The set of points reachable on time t will be those contained in the convex hull. You can do binary search or some vector calculations to find out what is the minimal t such that the target point lies inside it.
Hope it's clear.
Why does the editorial not mention anything regarding binary search? is it using a different logic?
Div 1 D.
Very Nice question.. I never did a bfs using a RMQ tree before. Cool!!
Thanks for the question
For Div1.E:
"The overall strategy is: if it is possible to move to vertex better than current, you should move to it, otherwise stay in place."
Can anybody prove it?
For div2 C, some people did something seemingly very simple, but I have no idea why something like the following works:
Div1 A / Div2 C anyone tried using binary search ?? I have an idea, but I ain't getting how to go forward. Let us say the minimum number of moves required to sort the whole array is M. clearly, for any number of moves less than M,we can't sort. Now, for any number of moves greater than M, we can always sort the whole array ( keep removing element from the end and place it on the end ). Thus, I think it is valid to say that the number of moves M can be binary searched. Now, I can't understand how to move forward, i.e. given number of moves, how to check if sorting can be done ? Also, I would like to know if my method is correct or not ?
Maybe you can check all subarrays (after sorting) Of size N-M (if you will move M elements then N-M will be left) And check if it's possible to find any one subsequence whose size is >=N-M and they form a subarray of sorted array
Now think about how to do that... I haven't thought about it but maybe this should work...
Hmmm......I understood what you are saying,but does that mean "what ever I do, I must find the longest increasing subsequnce " ? Because even after using binary search, you are actually finding the longest increasing subsequence (in the step when optimal value of M is found). So, won't that make binary searching useless ( as we could directly find the answer by finding longest increasing subsequnce ) ?
Nope maybe you can use sliding window on vector pair ( value,index) and check if there exist a susequence in given array forming subarray in sorted array
For problem B lazy student first of all, let's consider what we do in order to construct an MST.
1)Sorting all the edges in ascending order of their weight. 2)Pick the smallest edge(not selected till now)check whether it forms a cycle or not. If it doesn't form a cycle include it in the spanning tree else discard it. 3)Repeat step 2 until we have got V-1 edges in the spanning tree. 4)The spanning tree that we have now is the MST.
This same thing is written in the editorial first of all sort the edges in ascending order, then if the current edge needs to be included in the MST include it else if the edge is supposed to be discarded from the MST then it must form a cycle in the spanning tree constructed till now otherwise it would contradict the condition of getting discarded which is an edge is discarded if and only if it forms a cycle in the spanning tree constructed till now. If the edge to be discarded doesn't form a cycle then a graph having a corresponding spanning tree given would not exist. my submission=>https://codeforces.com/problemset/submission/605/94260114