If the given n is odd the answer is 0, because the perimeter of any rectangle is always even number.
If n is even the number of rectangles which can be construct equals to n / 4. If n is divisible by 4 we will count the square, which are deprecated, because we need to subtract 1 from the answer.
Asymptotic behavior — O(1).
At first let's find the minimum in the given array and store it in the variable minimum. It is easy to understand, that we always can paint n * minimum squares. So we need to find such a minimum in the array before which staying the most number of elements, which more than the minimum. In the other words we need to find 2 minimums in the array which are farthest from each other (do not forget about cyclical of the array). If there is only one minumum we need to start paint from the color which stay in the array exactly after the minimum (do not forget about cyclical of the array too). It can be done with help of iterations from the left to the right. We need to store the position of the nearest minimum in the variable and update her and the answer when we meet the element which equals to minimum.
Asymptotic behavior — O(n), where n — the number of different colors.
Let's build the answer recursively. For k = 0 the answer is - 1 or + 1. Let we want to build the answer for some k > 0. At first let's build the answer for k - 1. As the answer for k let's take four copies of answer for k - 1 with inverting of values in last one. So we have some fractal with 2 × 2 base: 00, 01. Let's prove the correctness of such building by induction. Consider two vector from the top (down) half: they have zero scalar product in the left half and in the right, so the total scalar product is also equals to zero. Consider a vector from the top half and from the down: their scalar products in the left and the right halfs differs only in sign, so the total scalar product is also zero.
Note the answer is also is a matrix with element i, j equals to \texttt{+} if the number of one bits in number i|j is even.
Complexity O((2k)2).
At first let's unite all segments which are in same verticals or horizontals. Now the answer to the problem is the sum of lengths of all segments subtract the number of intersections. Let's count the number of intersections. For this let's use the horizontal scan-line from the top to the bottom (is can be done with help of events — vertical segment is open, vertical segment is close and hadle horizontal segment) and in some data structure store the set of x-coordinates of the open segments. For example we can use Fenwick tree with precompression of the coordinates. Now for current horizontal segment we need to take the number of the opened vertical segmetns with value x in the range x1, x2, where x — vertical where the vertical segment are locating and x1, x2 — the x-coordinates of the current horizontal segment.
Asymptotic behavior: O(nlogn).
Consider slow solution: for operations of the first type reassign all letters, for operations of the second type let's iterate over the symbols in s from left to right and maintain the pointer to the current position in alphabet permutation. Let's move the pointer cyclically in permutation until finding the current symbol from s. And move it one more time after that. Easy to see that the answer is one plus the number of cyclic movements. Actually the answer is also the number of pairs of adjacent symbols in s that the first one is not righter than the second one in permutation. So the answer depends only on values of cntij —- the number of adjacent symbols i and j.
To make solution faster let's maintain the segment tree with matrix cnt in each node. Also we need to store in vertex the symbol in the left end of segment and in the right end. To merge two vertices in the segment tree we should simply add the values in the left and in the right sons in the tree, and update the value for the right end of the left segment and the left end of the right segment.
Complexity: O(nk2 + mk2logn).










For C, the answer can be found easily if one already knows about Hadamard Matrix. :)
https://en.wikipedia.org/wiki/Hadamard_matrix
Wow! I had never heard of that. Thanks for sharing!
Thank you buddy
I read that in my Analog Subject.I wished i had paid attention to that at that time :(
Yes, I had not given the contest but it seems the problem has been taken from the september long challenge 2015 on codechef. For those who are actually interested to solve this problem with harder constraints, try this problem. (The problem may not seem actually same as the one given but once you mathematically or using program deduce the pattern in TERVEC, the problem becomes the same).
Here is a link to the question https://www.codechef.com/SEPT15/problems/TERVEC
It seems that both I and Hadamard thought the same...
Then kindly explain what both of you thought :D
I solved the problem during contest, but I have no idea why it worked. I just saw a pattern, and coded it :/ .
I can't prove its correctness. I can kind of verify it, but not a proof that it.
Well I can't rigorously prove it in English but have a look at the easy statement:
I'll look at the easy statement when I see it. The image isn't visible.
Actually, this is also the same diagram shown in iterative FFT (by the way, FFT and FWT are quite similar, only different in calculation step)
Please give links for FFT, FWT where I can understand this diagram. I assume ai is the coefficient of polynomial in FFT, but that's all I know.
Now I am curious, after reading this. What is the physical significance of a matrix's determinant? What does it signify about a matrix(I don't mean properties, I mean significance, eg: scalar product of force and displacement signifies the magnitude of work done in physics) .
Does anyone know this? If it's a very basic question, then I guess I've forgotten my school stuff.
Nice! Thanks for the great contest and fast editorial! ;D
Well, there seems to be a mistake in problem E's complexity. Shouldn't it be O(n * k^2 + (m * k^2)*logn)?
It will be fixed soon.
Anyway, thanks for the faaaaaaaaaaaaast editorial :P
,
Codeforces is very fast. It can process more than ~1e9 operation per second.
Do Codeforces servers belong to 22nd century or are they quantum computers?
They are quantum computers :) Programming Contest is just an excuse, Mike actually wants to test his quantum computers.
Are you sure? And if they "lie" with the execution time and give "bonus" time per run?
I had the same problem .... i tried to hack similar O(n) solution of kishan197 but unsuccessful . :(
me too :(
Asymptotic Big-O notation can be inaccurate especially when the program is extremely simple. But yes, it is very vague whether the hack will succeed. Personally, I also lost 50 points because of that code, but I don't feel that bad, since I knew that there was a good chance of resulting O(n) solution to pass thanks to the powerful optimizations.
Me too :(
If someone has a clean code for D, please share it. I could not implement the exact logic fast enough.
Dunno if it is neat but I have some comments 15054694
I finally finished mine. http://codeforces.com/contest/610/submission/15060370
I'm sorry, I don't get it. How does your variable
qwork? ThanksQ is for queries, it contains United vertical segments.
Great. How about
c? What is it used to store? UPD: Thanks for sharing your code. I understand.Thank you saurabhverma and VastoLorde95 for your comments. I was able to make myself clear!
VastoLorde95 I am going through your code. It would be great if you will clear a couple of things.
For a row type of point you are pushing in map "e" the starting and ending x coordinates of row : e[seg->fi] and e[seg->se+1]. Why not e[seg->fi] and e[seg->se]?
Can you just give an idea of how Fenwick tree is storing points based on map "f".
Thanks.
Let the row be [L, R]. This means that the row occupies all points from L to R inclusive and the segment does not exist point R + 1 onwards, hence we create two events — we add the segment to the list of active rows when we reach x = L and remove the segment from the list of active rows when we reach x = R + 1. If we were to remove the row at x = R itself, then it will give us a wrong answer if there exists another column at x = R which intersects with this row.
A Fenwick tree uses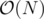 memory where N is the range of the tree. But since N can be as high as 2 × 109 (which is too big to fit in memory), we notice that there are at most 2 × 105 distinct values that the x co-ordinate can take and hence perform co-ordinate compression. f(x) is a function that maps the x co-ordinates in the range [ - 109, 109] to [0, 2 × 105]
memory where N is the range of the tree. But since N can be as high as 2 × 109 (which is too big to fit in memory), we notice that there are at most 2 × 105 distinct values that the x co-ordinate can take and hence perform co-ordinate compression. f(x) is a function that maps the x co-ordinates in the range [ - 109, 109] to [0, 2 × 105]
Got it! Thanks for the explanation!
can u explain how you have implemented sweep line , if not whts your logic and how you have implemented it , please dont be brief ...
Here is my take on this problem in Java
http://codeforces.com/contest/610/submission/15058416
The whole solution is in ~180 lines (including FenwickTree, Segment and Event classes), after that there is just my input reader and some unrelated to the problem functions.
http://codeforces.com/contest/610/submission/15056916 I don't know if you think it is clear
I solved it without using Coordinate Compression. I united all the overlapping segments and then used order statistics tree (read about policy based data structures in C++ STL). Method: Three types of events with the following priorities. ADD > QUERY > REMOVE. (This is important since all the points needed must be present during query).
Add — Add the y-coordinate to the tree Query — Query the order statistics of y_min and y_max+1 and do order(y_max+1)-order(y_min) Remove — Remove the y-coordinate from the tree.
The solution is quite long (nearly 120 lines). But I hope it will be clear. http://codeforces.com/contest/610/submission/15086077
Wow, that order statistic tree using STL is extremely useful !!! I didn't know about it. Now I can have a self-balancing BST in my template without attaching my AVL Tree's over 200 lines of code!
And, depending on the inserted keys, sometimes it's even faster than my AVL Tree implementation too! Thanks a lot!
Check these posts http://codeforces.com/blog/entry/11080 http://codeforces.com/blog/entry/13279 https://gcc.gnu.org/onlinedocs/libstdc++/ext/pb_ds/
Check these posts http://codeforces.com/blog/entry/11080 http://codeforces.com/blog/entry/13279 https://gcc.gnu.org/onlinedocs/libstdc++/ext/pb_ds/
You are welcome. By the way, Happy new year :)
That's great. Thanks.
Happy New Year!
D can be reduced to the classical union of rectangle areas problem
Could you give a more detailed explanation ?
This How to weep like a Sir blog by DanAlex should help, I believe. Frankly line sweep is a little beyond me at this point I believe that one of the entries in the article is very relevant.
thanks:)
What is this classical problem? It maybe uses line sweep, but what is the problem?
Given n rectangles whose sides are parallel to the coordinate axes find the union of the area of the rectangles.
It is used as an example in many line sweep tutorials so for this reason I consider it classical.
do you have any implementation of that..
Can someone tell me where am wrong in this Div2 B problem : http://codeforces.com/contest/610/submission/15053920
long long temp=min_value*n;should belong long temp=min_value*1ll*n;Thank u :)
I have a faster to submit solution on D. Google Lightoj 1120 and open this — https://github.com/lamphanviet/competitive-programming/blob/master/light-online-judge/accepted-solutions/1120%20-%20Rectangle%20Union.cpp :)
This is crazy= =
Pardon my inexperience, but does the solution use a combination of line sweep and segment tree for the y-axis? Thanks.
If you talk about author solution, yes, but who cares, this works too :D
610E: Complexity: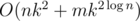 I think it was something wrong?
I think it was something wrong?
Yes the formulas parsed in a wrong way. Alex will fix it soon.
What are some possible alternative approaches for E? I see multiple solutions using <15 mb of memory, some of them even without segment tree — but with some sets instead.
I did it with sqrt-decomposition, it takes O(sqrt(n) * k2) memory.
We can achieve O(log n) per modification, and O(k^2) per query. Just use a set to maintain the segments containing same characters.
Could you elaborate please?
Suppose we have a map representing a sequence of segments with equal characters (maps right border to a character).
Then for each segment modification we:
my code: http://codeforces.com/contest/610/submission/15151605
Please show your code, thanks.
For C: "It's guaranteed that the answer always exists. "
If k == 0, there is no "scalar product" and there is no answer at all, but it seemed that k == 0 is checked and the expected output must be "+" or "*". Should we output "*" or "+" when there is no answer?
My WA submission
If the code print '*' or '+' when k == 0, it will be accepted.
Well, because there are no pairs to produce a "scalar product" when k == 0, we should output any set of one vector. So '*' and '+' are fine.
But "It's guaranteed that the answer always exists. " When there is no anaswer, "0" can't be accepted but "*" and "+" can be accepted. Why? It would be fine if any other output can be accepted when there is no answer.
I think that '0' is not accepted, because '0' isn't a vector in this problem. I mean, you cant print 'welfihwogiwe', because it's just not a vector, and you have to print a set of vectors.
The rule: "It's guaranteed that the answer always exists. " Neither "0" nor "*" can be accepted since there is no solution.
But if we accept any other output when k == 0, we does not break the rule though this is not necessary. "Any other output" is just a workaround to keep that rule without removing "k=0".
I think it would be better if "k==0" can be removed.
Why do you think there's no solution? There are two possible solutions — "*" and "+" :)
I had thought that "scalar product" rule should be applied to any solutions then there must be no solution if there is only one vector.
After I read the description again, I found that this rule should be used only if there are two vectors.
I am sorry for the misunderstanding.
Thank you all!
When k=0 there exists a valid set of vectors that satisfy the orthogonal requirements, which is either '*' or '+'. So it is not a "no answer" situation.
When k = 0, there is only one vector and there is no "scalar product". If we extend the definition, for example, we do scalar product with itself, we get 1*1 = (-1)*(-1) > 0. The only valid vector should be "0". But it is not the answer.
The orthogonal requirement is that "any two vectors are orthogonal". If there exists only one vector, "any two vectors are orthogonal" still holds.
Thanks. I read the description again: "find 4 vectors in 4-dimensional space, such that every coordinate of every vector is 1 or - 1 and any two vectors are orthogonal. "
So if there are no two vectors, we can print any vector and this does not break the requirement about two vectors or more.
I guess we were asked to output a set of basis. Even only one vector is ok.
Thank you! I have checked the statement and found that "scalar product" should only be used when there are two vectors in the answers. Sorry for my carelessness.
The contest is not about hiding solution in problem statements. k = 0 did not make a huge difference. I appreciate you have been providing many contests but not at the cost of poor and confusing problem statements.
In problem A, end to end is mentioned right in the end in the output section and no where perimeter is used. Now tell me one reason why I would not think of area.
Vacuous truth
I'm wondering why the constrains was N <= 2*10^5. I had the same solution as the author but with lazy propagation so it has twice the memory which didn't fit in the memory limit.
I was just wondering if that was intentionally? :P
I think the 512MB memory limit is quite sufficient for even a segment tree implementation that has redundant nodes and 10x10 attributes, lazy flag associated with each node.
For 2*10^5, I guess maybe Codeforces machines are so fast now so that we need to set a higher computational workload to take down TLE solutions :)
Actually my naive solutions works so fast that we have not any alternatives.
I just have to note that the English in this editorial is particularly bad, and I hope you would put a little more effort to translations, as most of this site's users can't speak Russian.
Can anyone pls point out what is wrong with this solution? Div 2B
I think the variable
ibefore thewhileloop should be initialized to 1 (instead of 0).Hope it helps!
I had a slightly different approach for B. We find the minimum element m and subtract it from each element of A[1...n]. Next, we find the length of longest continuous elements which are nonzero. Let this length be l . Then our answer is ~~~~~ ans = s1 — (s2 — l), where
s1 = sum of all elements in A[1...n] initially
s2 = sum of all elements in A[1...n] after subtracting m
We can find l using disjoint-set data structure . Here is my code~~~~~
please unblock problemset page
Can someone explain why some people use segment tree in problem D?
What are they storing there ?
It's used to store the open segments for a given range after compressing the coordinates.
Thanks! I'll look at your solution to try to understnad better.
I have a solution with sets and no segment trees for problem E. It takes O(n) memory and its complexity is O(qk^2). Here's the link if you're interested: 15058624
Explanation of problem C editorial is not clear :(
suppose, for 1 the initial matrix is
so, for k=2 u just copy the solution for k=1 in 4 copies and set them into the matrix for k=2.. the matrix will be like
just flip the 4th part(marked by arrow). the final output will be
do the same thing for next k....
wow..!!!!! THANKS!!!!!!!!!!!!!!!
D seems to be well known idea for some coders . Can anyone share some link to tutorials where i can learn the technique from . A little more detailed explanation may also help :)
It's about the Sweep Line technique, you can check it here and here.
You might also need order statistic trees, which are explained here (check Red-black trees)
Thanks i'll go through the links . May i PM you if i don't get something :)
Yep, sure :D
Can somebody please give a better explanation of the soultion for problem B? I don't get it :-? . It seems simple but something tricks me into giving wrong solutions.
Hello :) Yo can always iterate through whole circle M times, where M i the minimum of array (so M*N,where N is size of array). Then you have to find the largest piece of array without the minimum (and add this size to result) — there you go :)
I don't understand problem D, can anyone make it more clear? Does the problem just wants us to find the number of points all line segment covers? or, it needs to deal with area and square?
It's the same. If it covers x 1x1 points, then it has an area of x too.
Ok, now here's some confusion to me. If a point is (0,0,0,0) then does it contribute to the answer or not, because it has 0 area?
EDIT: I believe we must only find the number of points,a and not area of line segments. Because if we consider area, the answer of 1st case will be 6.
It's not lines we're talking about here, but squares of the grid. If a point is (0,0,0,0) in this problem, if we transform that to grid points coordinates (instead of grid squares), it would be (0,0,1,1). But there's no need to resort to that.
I guess what you're saying is, that we do have to count distinct points in this problem right? And when (if,ever) transforming to a grid, each point is visually magnified to look like a square instead of a point. What I think happens is, that the problem about finding union of areas gets reduced to problem of finding distinct points? If not, is there a easy way to solve union of areas problem, without considering them to be points?
It's like an infinite matrix and a point means a cell with the given coordinates :)
I know that, I just got confused with the word area :)
btw, that github link you provided in another comment, what is the working logic behind that code? It is so short, doesn't even does any segment merges.
BTW, Can anybody please answer I_love_Captain_America, I wonder the same thing :D
function2 can, but will he?
Why you change your handle P_Nyagolov? How many name changes can I remember?
Sorry if I confused you, it's just the way I picture this kind of problem in my head, I imagine squares instead of grid lines, it makes it easier to visualize. Just like P_Nyagolov says below, I picture an infinite matrix.
I am sorry, but the English version of this editorial needs some serious editing.
Do I the only one who use segment tree on D?QAQ
can you explain your solution
Expand the points to grids,then just figure out the area.
Where'd you learn this method? So nice and short. Please give a link to from where you learned this method.
To be honest it's not difficult to understand but not excellent enough :D.It is come up by a friend of mine.
I am obviously unfamiliar with it, and hence the difficulty in understanding. Please outline the logical steps, reason behind sorting the way you did, and I'll be less lost in your code.
well,do you know how to figure out the total area of lots of rectangles,whose sides areparallel to the axis and somewhere may be overlapped?
No, but since its a standard problem, I am looking at topcoder tutorial for this(not very detailed tutorial). So, where'd you learn from?
In some ways,I didn't learn from anyone it's come up myself during the contest:D
Maybe it's an ordinary method.
In fact, this method is very easy to understand, I also used this method.We can expand all segments 0.5 unit.And the rectangle area is the number of this segment covers.So, the answer is the area of all rectangles.We can use segment tree to solve it.
yup,here it is
Imagine you're explaining to a total newbie. This explanation is not enough for me. Please explain in a little more detail.
"expand all segments 0.5 unit"sounds good but doesn't better than replaced by the square on its top right coner
337B----I don't know why it's showing wrong answer at case number 7......the input is large so not being able to check it as well. did it the same way as the editorial. can any of you guys help me out? here is the link: https://ideone.com/hsCXCv
same problem with my code too. answer for problem B test case 7 is 207723124205, but my code giving 207723124204. Answer is differ by 1. plz find tht 1.
Generally speaking, I suggest to don't fix your solutions based on specific WA. You get much more experience trying to fix it in blind.
Coding D is a nightmare! 1. Merge segments 2. segment tree 3. line sweep + smaller stuff like compressing points.
So I have basically coded up everything necessary for D, but I still don't know an efficient way of merging the overlapping line segments. Is there some sort of standard way to do this?
Do you mean like merge horizontals with same Y?
If so:
Sort by (Y, X1)
Iterate from 1 to N-1
cur = line[i], last = line[i — 1]. If (cur.X1 <= last.X2) set last.X2 = cur.X2 and drop cur from list.
Thats how I did. O(NlogN) for sort and O(N) for merge.
Thank you! I considered this before hand, but for some reason thought it wouldn't work.
Ooops, btw I messed it up a bit. Instead of:
set last.X2 = cur.X2
you need:
set last.X2 = max(last.X2, cur.X2)