There are two ways to solve this problem.
The first is to hard-code numbers of days in months, check the first day of the year and then iterate over days/months — http://ideone.com/4TYPCc
The second way is to check all possible cases by hand. The 2016 consists of 52 weeks and two extra days. The answer for "x of week" will be either 52 or 53. You must also count the number of months with all 31 days and care about February. http://ideone.com/Bf9QLz
611B - New Year and Old Property
Each number with exactly one zero can be obtained by taking the number without any zeros (e.g. 6310 = 1111112) and subtracting some power of two, e.g. 6310 - 1610 = 1111112 - 100002 = 1011112. Subtracting a power of two changes one digit from '1' to '0' and this is what we want. But how can we iterate over numbers without any zeros? It turns out that each of them is of form 2x - 1 for some x (you can check that it's true for 6310).
What should we do to solve this problem? Iterate over possible values of x to get all possible 2x - 1 — numbers without any zeros. There are at most 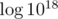 values to consider because we don't care about numbers much larger than 1018. For each 2x - 1 you should iterate over powers of two and try subtracting each of them. Now you have candidates for numbers with exactly one zero. For each of them check if it is in the given interval. You can additionally change such a number into binary system and count zeros to be sure. Watch out for overflows! Use '1LL << x' instead of '1 << x' to get big powers of two. http://ideone.com/Kfu8sF
values to consider because we don't care about numbers much larger than 1018. For each 2x - 1 you should iterate over powers of two and try subtracting each of them. Now you have candidates for numbers with exactly one zero. For each of them check if it is in the given interval. You can additionally change such a number into binary system and count zeros to be sure. Watch out for overflows! Use '1LL << x' instead of '1 << x' to get big powers of two. http://ideone.com/Kfu8sF
How would we solve this problem in O(wh + q) if a domino would occupy only one cell? Before reading queries we would precalculate dp[r][c] — the number of empty cells in a "prefix" rectangle with bottom right corner in a cell r, c. Then the answer for rectangle r1, c1, r2, c2 is equal to dp[r2][c2] - dp[r2][c1 - 1] - dp[r1 - 1][c2] + dp[r1 - 1][c1 - 1]. We will want to use the same technique in this problem.
Let's separately consider horizontal and vertical placements of a domino. Now, we will focus on horizontal case.
Let's say that a cell is good if it's empty and the cell on the right is empty too. Then we can a place a domino horizontally in these two cells. The crucial observation is that the number of ways to horizontally place a domino is equal to the number of good cells in a rectangle r1, c1, r1, c2 - 1.
You should precalculate a two-dimensional array hor[r][c] to later find the number of good cells quickly. The same for vertical dominoes. http://ideone.com/wHsZej
611D - New Year and Ancient Prophecy
By {x... y} I will mean the number defined by digits with indices x, x + 1, ..., y.
Let dp[b][c] define the number of ways to split some prefix (into increasing numbers) so that the last number is {b... c} We will try to calculate it in O(n2) or  . The answer will be equal to the sum of values of dp[i][n] for all i.
. The answer will be equal to the sum of values of dp[i][n] for all i.
Of course, dp[b][c] = 0 if digit[b] = 0 — because we don't allow leading zeros.
We want to add to dp[b][c] all values dp[a][b - 1] where the number {a... b - 1} is smaller than {b... c}. One crucial observation is that longer numbers are greater than shorter ones. So, we don't care about dp[a][b - 1] with very low a because those long numbers are too big (we want {a... b - 1} to be smaller than our current number {b... c}). On the other hand, all a that (b - 1) - a < c - b will produce numbers shorter than our current {b... c}. Let's add at once all dp[a][b - 1] for those a. We need  . Creating an additional array with prefix sums will allow us to calculate such a sum in O(1).
. Creating an additional array with prefix sums will allow us to calculate such a sum in O(1).
There is one other case. Maybe numbers {a... b - 1} and {b... c} have the same length. There is (at most) one a that (b - 1) - a = c - b. Let's find it and then let's compare numbers {a... b - 1} and {b... c}. There are few ways to do it.
One of them is to store hashes of each of n·(n + 1) / 2 intervals. Then for fixed a, b we can binary search the first index where numbers {a...} and {b... } differ. http://ideone.com/Rrgk8T. It isn't an intended solution though. Other way is to precalculate the same information for all pairs a, b with dynamic programming. I defined nxt[a][b] as the lowest x that digit[a + x] ≠ digit[b + x]. Now, either nxt[a][b] = nxt[a + 1][b + 1] + 1 or nxt[a][b] = 0. http://ideone.com/zczsc3
611E - New Year and Three Musketeers
The answer is - 1 only if there is some criminal stronger than a + b + c. Let's deal with this case and then let's assume that a ≤ b ≤ c.
Let's store all criminal- s in a set (well, in a multiset). Maybe some criminals can be defeated only by all musketeers together. Let's count and remove them. Then, maybe some criminals can be defeated only by b + c or a + b + c (no other subsets of musketeers can defeat them). We won't use a + b + c now because it's not worse to use b + c because then we have the other musketeer free and maybe he can fight some other criminal. Greedily, let's remove all criminals which can be defeated only by b + c and at the same time let a defeat as strong criminals as possible. Because why would he rest?
Now, maybe some criminals can be defeated only by a + c or b + c or a + b + c. It's not worse to use a + c and to let the other musketeer b defeat as strong criminals as possible (when two musketeers a + c fight together).
We used a + b + c, b + c, a + c. We don't know what is the next strongest subset of musketeers. Maybe it's a + b and maybe it's c. Previous greedy steps were correct because we are sure that 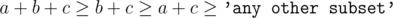 .
.
Now in each hour we can either use a, b, c separately or use a + b and c. Let's say we will use only pair a + b and c. And let's say that there are x criminals weaker than a + b and y criminals weaker than c. Then the answer is equal to 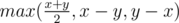 . The explanation isn't complicated. We can't be faster than
. The explanation isn't complicated. We can't be faster than 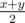 because we fight at most two criminals in each hour. And maybe e.g. y (because c is weak) so c will quickly defeat all y criminals he can defeat — and musketeers a + b must defeat x - y criminals.
because we fight at most two criminals in each hour. And maybe e.g. y (because c is weak) so c will quickly defeat all y criminals he can defeat — and musketeers a + b must defeat x - y criminals.
Ok, we know the answer in O(1) if we're going to use only a + b and c. So let's assume it (using only these two subsets) and find the possible answer. Then, let's use a, b, c once. Now we again assume that we use only a + b and c. Then we use a, b, c once. And so on.
What we did is iterating over the number of times we want to use a, b, c. http://ideone.com/R3Oy3F
Let's not care where we start. We will iterate over robot's moves.
Let's say the first moves are LDR. The very first move 'L' hits a wall only if we started in the first column. Let's maintain some subrectangle of the grid — starting cells for which we would still continue cleaning. After the first move our subrectangle lost the first column. The second move 'D' affects the last row. Also, all cells from the last row of our remaining subrectangle have the same score so it's enough to multiply the number of cells there and an index of the current move. The third move 'R' does nothing.
Let's simulate all moves till our subrectangle becomes empty. To do it, we should keep the current x, y — where we are with respect to some starting point. We should also keep maxx, maxy, minx, miny — exceeding value of one of these four variables means that something happens and our subrectangle losts one row or one column.
But how to do it fast? You can notice (and prove) that the second and and each next execution of the pattern looks exactly the same. If we have pattern RRUDLDU and the first letter 'U' affects out subrectangle in the second execution of the pattern, then it will also affect it in the third execution and so on. If and only if.
So, we should simalate the first n moves (everything can happen there). Then, we should simulate the next n moves and remember all places where something happened. Then we should in loop iterate over these places. Each event will decrease width or height of our subrectangle so the complexity of this part is O(w + h). In total O(w + h + n). http://ideone.com/xrU9u2
CHALLENGE FOR PROBLEM F (CLEANING ROBOT) — I was considering an alternative version of this problem, harder one. The same constraint for n but this time h, w ≤ 109. Describe a solution in comments and optionally implement it (it should get AC on this problem, right?). I will mention here the first person to solve this challenge.
We are given a polygon with vertices P1, P2, ..., Pn. Let Poly(i, j) denote the doubled area of a polygon with vertices Pi, Pi + 1, Pi + 2, ..., Pj - 1, Pj. While implementing you must remember that indices are in a circle (there is 1 after n) but I won't care about it in this editorial.
We will use the cross product of two points, defined as A × B = A.x·B.y - A.y·B.x. It's well known (and you should remember it) that the doubled area of a polygon with points Q1, Q2, ..., Qk is equal to Q1 × Q2 + Q2 × Q3 + ... + Qk - 1 × Qk + Qk × Q1.
Let smaller denote the area of a smaller piece, bigger for a bigger piece, and total for a whole polygon (cake).
smaller + bigger = total
smaller + (smaller + diff) = total
diff = total - 2·smaller (the same applies to doubled areas)
And the same equation with sums: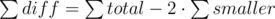 where every sum denotes the sum over
where every sum denotes the sum over 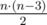 possible divisions.
possible divisions.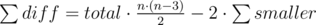
In O(n) we can calculate total (the area of the given polygon). So, the remaining thing is to find 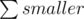 and then we will get
and then we will get 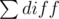 (this is what we're looking for).
(this is what we're looking for).
For each index a let's find the biggest index b that a diagonal from a to b produces a smaller piece on the left. So, 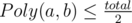 .
.
To do it, we can use two pointers because for bigger a we need bigger b. We must keep (as a variable) the sum S = Pa × Pa + 1 + ... + Pb - 1 × Pb. Note that S isn't equal to Poly(a, b) because there is no Pb × Pa term. But S + Pb × Pa = Poly(a, b).
To check if we should increase b, we must calculate Poly(a, b + 1) = S + Pb × Pb + 1 + Pb + 1 × Pa. If it's not lower that 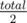 then we should increase b by 1 (we should also increase S by Pb × Pb + 1). When moving a we should decrease S by Pa × Pa + 1.
then we should increase b by 1 (we should also increase S by Pb × Pb + 1). When moving a we should decrease S by Pa × Pa + 1.
For each a we have found the biggest (last) b that we have a smaller piece on the left. Now, we will try to sum up areas of all polygons starting with a and ending not later than b. So, we are looking for Z = Poly(a, a + 1) + Poly(a, a + 2) + ... + Poly(a, b). The first term is equal to zero but well, it doesn't change anything.
Let's talk about some intuition (way of thinking) for a moment. Each area is equal so the sum of cross products of pairs of adjacent (neighboring) points. We can say that each cross product means one side of a polygon. You can take a look at the sum Z and think — how many of those polygons have a side PaPa + 1? All b - a of them. And b - a - 1 polygons have a side Pa + 1Pa + 2. And so on. And now let's do it formally:
Poly(a, a + 1) = Pa × Pa + 1 + Pa + 1 × Pa
Poly(a, a + 2) = Pa × Pa + 1 + Pa + 1 × Pa + 2 + Pa + 2 × Pa
Poly(a, a + 3) = Pa × Pa + 1 + Pa + 1 × Pa + 2 + Pa + 2 × Pa + 3 + Pa + 3 × Pa
...
Poly(a, b) = Pa × Pa + 1 + Pa + 1 × Pa + 2 + Pa + 2 × Pa + 3 + ... + Pb - 1 × Pb + Pb × Pa
Z = Poly(a, a + 1) + Poly(a, a + 2) + ... + Poly(a, b) =
= (b - a)·(Pa × Pa + 1) + (b - a - 1)·(Pa + 1 × Pa + 2) + (b - a - 2)·(Pa + 2 × Pa + 3) + ... + 1·(Pb - 1 × Pb) +
+ Pa + 1 × Pa + Pa + 2 × Pa + ... + Pb × Pa
The last equation is intentionally broken into several lines. We have two sums to calculate.
The first sum is (b - a)·(Pa × Pa + 1) + (b - a - 1)·(Pa + 1 × Pa + 2) + ... + 1·(Pb - 1 × Pb). We can calculate it in O(1) if we two more variables
sum_productandsum_product2. The first one must be equal to the sum of Pi × Pi + 1 for indices in an interval [a, b - 1] and the second one must be equal to the sum of (Pi × Pi + 1)·(i + 1). Then, the sum is equal tosum_product * (b + 1) - sum_product2.The second sum is Pa + 1 × Pa + Pa + 2 × Pa + ... + Pb × Pa = SUM_POINTS × Pa where SUM_POINTS is some fake point we must keep and SUM_POINTS = Pa + 1 + Pa + 2 + ... + Pb. So, this fake point's x-coordinate is equal to the sum of x-coordinates of Pa + 1, Pa + 2, ..., Pb and the same for y-coordinate. In my code you can see variables
sum_xandsum_y.
Implementation. http://ideone.com/RUY5lF
611H - New Year and Forgotten Tree
There are at most k = 6 groups of vertices. Each grouped is defined by the number of digits of its vertices.
It can be probed that you can choose one vertex (I call it "boss") in each group and then each edge will be incident with at least one boss. We can iterate over all kk - 2 possible labeled trees — we must connect bosses with k - 1 edges. Then we should add edges to other vertices. An edge between groups x and y will "kill" one vertex either from a group x or from a group y. You can solve it with flow or in O(2k) with Hall's theorem. http://ideone.com/7KuS1l











I read incorrectly statement of C ;_; and ended up solving wrong problem >.< . How can we tell the number of dominos that can be placed in rectangle r1 c1 r2 c2?
Found that so many people passed D.
What did you do to solve this problem?
(The editorial is really nice, and I wonder if there are any other ideas?)
In D, you've written: Of course, dp[b][c] = 0 if digit[0] = 0 — because we don't allow leading zeros.
Shouldn't it be digit[b] = 0 ?
sure, thanks
Fast and great tutorial,thanks you!
A — New Year and Days
I didn't read clearly . I think the first day of a week is Sunday... Very pitiful .
At first i thought it was 2015,but when i checked the calendar and found out the sample was wrong,thank god I did not make a mistake
why this greedy failed for problem e??
if(a+b>c) --> remove as per the previous rules else --> try to remove element less than equal to c, try to remove element less than equal to b ... if element is removed try to remove element closer to a else try to remove element less than a+b
It should work, my code passes doing this greedy. See below for a "proof". (I think it's correct, but not 100% sure)
Ok, so I read your code. You make the following error.
You eliminate everything that if between c + 1 and a + b which is correct.
Afterwards, you ONLY use (a, b, c) which is wrong. You should instead delete c, then delete a, b if possible, and if not, just delete a + b as it is larger.
Example test case that you might fail on:
2 5 6 10 10 10
You'll print 2 (I think?) while the answer is clearly 1.
Thanks..dont know why i overlooked the possibility of same thing for a+b<c in a+b>c case
Alternate approach on E that uses only greedy all the way:
Toss everything in a set. This will make deleting things very easy.
WLOG a ≤ b ≤ c, so then a + b + c ≥ b + c ≥ a + c ≥ max(c, a + b).
Therefore, greedy away using a + b + c, then the pair (b + c, a), then the pair (a + c, b), until the largest element is at most max(c, a + b).
Now we distinguish 2 cases:
Case 1: a + b > c. Then greedy using the pair (a + b, c), as the largest elements remaining can only be taken using this pair. Now all remaining elements are at most c. At this point, we'll fnish as in Case 2.
Case 2: c ≥ a + b. In other words, all remaining elements are at most c. Then every time we will take a c, i.e. the largest remaining element. Now we have to decide when to take (a, b) and when to take a + b. At each step, if there is an element that is ≤ b in our set, I claim that we might as well take (a, b). The proof is: in the future this element will be taken by something. If it's taken by a or b that's fine. If it's taken by a + b, we might as well have taken it with a b and then used the a for something else. If it's taken by c, you might as well have taken it with b, and let c take any remaining element.
So only greedy is enough to finish.
Am I only the guy who solved E with binary search? It seemed for me a bit easier and straightforward than greedy solution. In the search we try to find lowest time musketeers can defeat criminals. For each particular fixed time we use 7 counters (a, b, c, ab, ac, bc, abc) and greedy approach. Iterate through all criminals starting from more strongest and try to assign for each the musketeers squad if possible in the following order: a, b, c, ab, ac, bc, abc. In that case I don't even need to check whether c > ab. My submission
That is still greedy though. Cause you greedily assign them to a, b, c, ab, ac, bc, abc.
Yes, I agree. Bin search + gready.
Could you explain this line:
if (va + vac + vabc + vab < m && mas[i] <= a) va++;I think thatva= how many times you use(a)to defeat criminals. Why do you sumva, vac, vabc, vabtogether?Because (a) is used in the following team combinations: a, ab, ac and abc. We have separate counter for each group: va, vab, vac, vabc. So, if (a) overall is used less than (m) times, we can use it, otherwise we can't.
Do you mean we can't use
amore than(m)times?Yes. Because
mis the binary search step and it denotes number of hours enough for musketeers to defeat criminals. Andadenotes one of the musketeer (weakest one) and it can't spent more thanmhours fighting alone or as a part of the team.I get va++ , vb++ and vc++ from previous comments. But I do not understand the next three statements. Mainly the conditional part.
What does this actually check?
" va + vb + vab + vac + vbc + vabc < m "
Hi, I think that, although it passes in the tests, your code gives the wrong answer for the following sample:
3 38 48 72 73 89 97
It answers 3 but the answer is 2
I am sorry, your code is right. I understood the problem wrong.
For problem C, O(10^10) did not pass but it should have passed in 3s. I know solution of O(10^7) exists but why O(10^10) didnt pass? Can anybody tell me how much order can pass in 3s. Solution link: http://codeforces.com/contest/611/submission/15128001
Why do you think 10^10 should have passed in 3 seconds? That is simply too many operations, it is no surprise that it did not pass.
Not to mention that in fact your solution is doing 10^5 * 500 * 500 operations, which is actually 2.5 * 10 ^ 10, so even worse than you are thinking.
I believe 10**8 operations per second is average
There is also a solution with O(hlogh + wlogw + n) complexity for problem F.
I've skipped the third part and wrote O(h log hw + w log hw), got TLE. Added inline's — after contest — accepted. >_<
Solved D with string comparison in with suffix automaton and LCA... 15118514
with suffix automaton and LCA... 15118514
Could someone explain G with more details?
deleted
Seems like invalid memory access in line 47. The indices you use there seem completely mixed up, and in some cases the index may even evaluate to -1.
Cheers!
Could someone tell me why the correct answer for "1 100" is "1" at problem B? I don't really know what's wrong with my solution.
Link: http://codeforces.com/contest/611/submission/15114734
Correct answer is 16. ~~~~~ Participant's output 1 Jury's answer 16 ~~~~~
I have found an alternative solution to problem F, in complexity O(nlog(n)), like this:
First, let's pre-compute the minimum number of moves to get to a certain relative coordinate. We will have 4 arrays, MinPosX, MinPosY, MinNegX, MinPosX, where for example MinPosX[d] is the minimum number of moves after which the coordinate X will have increased by d. I leave the pre-comp part as an exercise. You can also look at my source below for hints.
Let's fix one coordinate (say the row), namely i. Then, the number of moves is bounded by min(MinNegY[i], MinPosY[n - i + 1]) (it is easy to see why). Actually, for a coordinate set (i, j), the value is min(MinNegY[i], MinPosY[n - i + 1], MinNegX[j], MinPosX[m - j + 1]). We have 2 of the values fixed. Now, it is easy to see / prove that MinNegY, MinPosY are monotonically increasing arrays, so we can binary search where the min transitions from MinNegX[j] to min(MinNegY[i], MinPosY[n - i + 1]) to MinPosX[m - j + 1]. There are some special cases, where the middle one does not exist.
Source code: http://codeforces.com/contest/611/submission/15129711
I have done the same but getting wrong answer
Can you tell me why am i getting wrong answer? http://codeforces.com/contest/611/submission/15130593 Idea is same as yours
In D, Shouldn't it be nxt[a][b] = nxt[a + 1][b + 1] + 1 instead of "-1" Errichto ?
Yes, I also have the same question :)
you are right, it should be "+1". Thanks
Thanks. And I'd like to thank you even more for setting up such great contests and finding time to put up such great editorials... Seems surreal how much time you have in a world where people don't even have time for their own families :) ... Have a great new year Errichto !!
In the problem D's solution, I think you should write
nxt[a][b] = nxt[a+1][b+1] + 1instead ofnxt[a][b] = nxt[a+1][b+1] - 1. Because you have denotednxt[a][b]as the lowest number x, such thatdigit[a+x] != digit[b+x]. Am I right?In problem D , Can someone explain me the use of nxt[a][b] should be nxt[a+1][b+1] or 0 with some example and why do need it ? Thanks.
Why do we need it? When we compare two numbers of the same length, e.g. 234569 and 234860 we care about the first place with two different digits. In this sample 4-th digits differ.
nxt[a][b]assumes that one number starts at index a and the other numbers starts at index b. Then, it tells us where is the first place with different digits. In other words, it tells us the smallest non-negative i that digit[a + i] ≠ digit[b + i].Now, let's understand "zero or nxt[a+1][b+1]+1". What happens when
digit[a] != digit[b]? Then an arraynxt[][]should tell us that i = 0. So nxt[a][b] = 0. Otherwise, it's enough to take a look into nxt[a + 1][b + 1]. It is the smallest non-negative j that digit[a + 1 + j] ≠ digit[b + 1 + j]. So, we can say that now the smallest i is equal to i = 1 + j = 1 + nxt[a + 1][b + 1].This is a very important comment. I'd include it in the main text, or at least made a reference.
Thanks for the explanation
So why is it
x = nxt[a+1][b+1]in the code snippet and notnxt[a+1][b+1] + 1? And shouldn't it beif(t[a] != t[b]) x = 0instead ofif(t[a] != t[b]) x = a?where?
In the code snippet http://ideone.com/zczsc3
Oh, sorry for that.
nxt[a][b]has a bit different meaning in my code. If digit[a] ≠ digit[b] then nxt[a][b] = a. If digit[a + 1] ≠ digit[b + 1] then nxt[a][b] = a + 1. And so on.In other words, nxt[a][b] from my code is equal to a + nxt[a][b] from the editorial
Ok, thanks :)
It may be good to write it in the editorial itself. :)
Besides, could you please point me to some resource so that I could learn what the idea behind hashing is? I'm still learning and I never came across it. Thanks
It think that it'd be better to strengthen the neural pathways you've just established :)
I mean, we need to connect the concepts together so they support each other whenever you are faced with a different problem.
The big picture behind this problem is the concept of suffix array. This problem addresses the specific part of that bigger concept — the longest common prefix concept. I understood this only after reading the submission 15113502.
From my point of view, it is better to attack this single concept from different angles, cause the stuff is pretty basic. If you are going after hashing, you are at risk of losing the essential empirical evidence in the face of the brain for the necessity to retain the lcp concept on educationally relevant time scale.
But, probably, I am wrong.
instead of nxt[a][b] we can use lcs[a][b] (longest common substring starting from a and b to the end) and check if the length >= intended length it will make the same job of nxt[][] right ?
I think it's a wonderful goodbye round and I will never forget it because it is my first goodbye round.Thank you a lot,Errichto!!!
For problem B, can someone please explain the reason behind the condition
(1LL << i) / 2 <= binside the for loop in the solution provided (link) ? What would have been the effect if the condition wasfor(int i = 0; (1LL << i) <= b; ++i). I can't understand the importance of/2Thanks.Maybe 2i > b but 2i - 1 - 2j ≤ b. It means that with condition 2i ≤ b we would miss some solutions.
I claim that 2i - 1 - 2j ≥ 2i / 2. It's true because j ≤ i - 2. So, we have the following two inequalities"
Thus, we have b ≥ 2i - 1 - 2j ≥ 2i / 2 and I can write
(1LL << i) / 2 <= b.If your 'b' will be like 2^k — 1, you'll not calculate 2^k — 2 and some another numbers. For example: 1 7
Could someone explain G with more details?
I will do it but not today
Can someone look at my code on E?
http://codeforces.com/contest/611/submission/15137943
I couldn't find any bug :( My greedy can be wrong but it finds smaller answer, so there must be some bugs. Thanks for help.
Here is a small test case -- your answer is 2, the correct one is 3:
You can beat the first criminal with A+B, the second one with A+C, and the third one with B+C. Yet, you need at least three hours.
I'm really grateful about reply. I never think like that :(
tourist replays .. what a moment ! :D
Good Bye 2015 on Problem E Pretest 10 :)
Attempt to Problem F: (Sorry for large picture)
The problem with original solution is that we cannot simulate all O(w + h) steps now. Instead, let's consider the sequence of reducing the rectangle be R, and after two runs we have a w * h rectangle left. (w, h > 0, or we can end earlier)
Four directions are troublesome, so we consider R to be either Vertical or Horizontal.
For example, the above picture illustrates a VVHVH sequence.
Let t1...t|R| be the timestamp of when the i th move takes place, then, the contribution to answer of each piece is written as follows ( + 2n part omitted)
How about, after 2nd round? Looks similar to 1st round: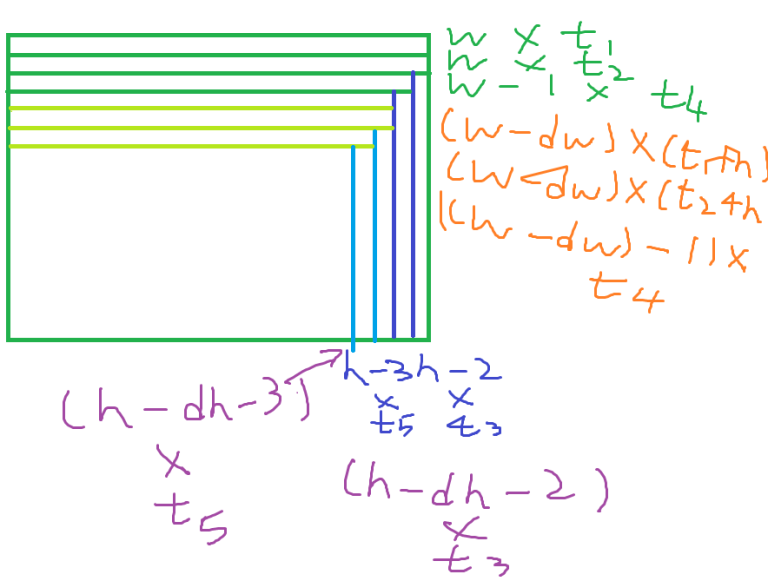 (dh is the total decrement of h after a round, dw similar)
(dh is the total decrement of h after a round, dw similar)
(I forgot the + n part for t3..5, but I hope you got the idea)
let's focus on the topmost pieces of each round, their contribution is of course (w * t1), (w - dw) * (t1 + n), (w - 2dw) * (t1 + 2n).... (w - kdw) * (t1 + kn) where (k + 1) is the number of round lasted.
How to sum it? Let's do some sum Getting rid of w * t1: sum of them is (t1)(w + (w - dw) + (w - 2dw)..(w - kdw), the right part can be summed using Arit Sequence. So the remaining job is to sum (w - dw) * (n) + (w - 2dw) * (2n) + ... + (w - kdw) * (kn), which is equal to (w - dw) * n + (2w - 4dw) * n + (3w - 9dw) * n..., the first term (w part) is just 1 + 2 + 3 + 4 + 5..., the second term (dw) is (1 + 22 + 32 + 42 + ...) = k(k + 1)(2k + 1) / 6. Both can be calculated in O(1), and then we multiply it by n and add to the first part, then this piece is done once we know k.
How about those (w - 1), (w - 2).. piece? looks so annoying, but we can just rewrite w' = w - 1, w' = w - 2... and we're all good. Same applies to height pieces.
Getting k is not difficult either. One easy way is to take k = min(remainingh / dh, remainingw / dw), and then we know k. The remaining part can be handled by a final enum, as we know that we'll end in less than or equal to one turn.
Happy New Year! Conceptually looks easy to me, so I'm wondering if I made something wrong.
15140553 Code for reference. Sorry for ugly code (Idk why i use a Priority Queue to sort indexes LOLZ) Also should be pretty fast.
Morning news: last night a unitconvert website got DDOSed, the attack seems to be from all around the world. The attack was at 16:35 UTC, specialists say "number of mondays in 2016" was the common search used to over-bulk the servers, stay tuned as we find out the organization behind this.
In problem D tourist http://codeforces.com/contest/611/submission/15107147 Why he(tourist) is adding the value
dp[i — len][i — 1] to the value sum (when added == false) after updating dp[i][j] = sum; ( after updating sum if that number is smaller than that ) why do we need this part, can someone explain ?
if (i — len >= 0 && !added) { add(sum, dp[i — len][i — 1]); } Thank in advance.
"One of them is to store hashes of each of n·(n + 1) / 2 intervals"
What are the hashes of the intervals? I've never used such a thing. The only hashes I've used are the md5/sha1 hashes.
thanks
He was talking about Rolling hash. It is useful for string comparison, because it can be calculated very fast for neighbour substrings. If two strings have same hash, they are very likely equal and comparing numbers is much easier than comparing strings.
I solved E with branch and cut LP: 15130924. The idea is you create 8 variables corresponding to a, b, c, ab, ac, bc, abc, and total time. Then the problem can be expressed as a set of linear inequalities on these variables.
I have no proof that it works, though. Maybe it runs for a very long time on some input.
Detailed editorial for G (geometry) is added.
Fairly unnecessary solution on H, but I'll post it here anyways.
Let G1, ..., Gk be the groups. Let EGiGj be the edges we need to make between groups Gi and Gj. WLOG EGiGi = 0 since we can take care of those immediately at the beginning.
Claim: A necessary and sufficient condition for checking whether the answer exists can be described by the following. Take any subset of the groups. Let E be the sum of the edges between those groups and only those groups. Let V be the number of total vertices in those groups. If for all subsets satisfying V > 0, E ≤ V - 1 then an answer exists.
Proof: We prove this by induction and an algorithm. We separate 2 cases.
Case 1: Some group G has size ≥ 2. I claim that there exists a different group H such that EGH ≥ 1 and decreasing the group size of G by 1 maintains the condition.
First, ignore all groups H that have no edges needed between G and H. So from now on only consider G and the groups that G needs an edge between. Let S be any subset of the groups that includes G. Call a subset S "tight" is the total number of vertices in S is exactly 1 more than the total number of edges in S.
Now all we have to show is that there exists some group H in every tight subset. Then drawing an edge from G to H and reducing the size of G by 1 clearly maintains the condition. By reducing the size of G, I mean saying that the vertex in G that we drew an edge to will no longer be used in further edges. This guarantees that we have a tree in the end.
Lemma: If S1, S2 are tight, then is tight.
is tight.
Proof: Let V(S) denote number of vertices in a group, E(S) denote number of edges among a group. The number of vertices in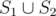 is equal to
is equal to 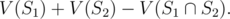
Now, because S1 and S2 are tight,
But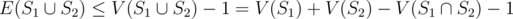 .
.
Combining this with the previous,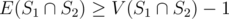 , which implies that
, which implies that  is tight.
is tight.
Now if no group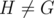 is in every tight subset, then the intersection of all tight subsets is just G itself, which is a contradiction to the definition of tight, as V(G) ≥ 2, but there are no edges needed between G and itself.
is in every tight subset, then the intersection of all tight subsets is just G itself, which is a contradiction to the definition of tight, as V(G) ≥ 2, but there are no edges needed between G and itself.
Case 2: G has one vertex.
If G has at least 2 edges adjacent to it (needed between it and other groups), ignore it. Otherwise, it has exactly one edge adjacent to it, and just use that edge. In other words, reduce the size of G to 0 and draw the edge. This clearly maintains the condition I described above. So the proof is complete.
Alternatively, do Case 1 until all groups of size 1 and then brute-force spanning trees.
Alternative solution for problem D:
let dp(L, R) = number of ways to use number(L, R)
having number(L, R) you need to have number(R + 1, P) for all P >= R+1 and number(L, R) < number(R+1, P) and R < N.
there is an index P >= R+1 where number(L, R) < number(R+1, P) so we can update dp(R+1, P) += dp(L, R) for each P (range update).
the answer is the sum of dp(L, N-1) for each L.
The trick is that all range updates can be done in constant time, see 15196533
In problem E the answer using only a + b and c should be max(max(x, y) / 2, x – y, y – x).
Can anyone please explain why my following solution for C fails???
My Submission
Really need help. I am quite baffled.....
I have written a more detailed editorial about 611 C, "New Year and Dominos" here. Please refer it and ask me any doubts. :)
Thanks , that helps me a lot to understand the editorial :)
Why am I getting WA on Test case 72 for problem B : 85538392
While the very similar solution gets accepted: 85538021
Does it have to do something with pow()?