A. Naive solution in O(n) (some simulation all of n rounds) gets TL. Let's speed up this solution. Let's consider rounds on segments [1..mk], [mk+1..2mk], [2mk+1..3mk] and so on. You can see that results of games on these segments will repeat. So you can simulate over exactly one segment and then take into consideration them [n/(mk)] times ([x] is rounding down). Remainder of n%(mk) last rounds you can simulate separately. So you have O(mk) solution that easily fits into time limits.
Authors are Ripatti and Gerald .
B. In this problem you should build bipartite graph with n+m vertices. All vertices of the firts part correspond to the rows of the table, vertices of the second part correspond to the columns of the one. Edge connects vertices iff some regular column is placed in the cross of corresponding row and column.
Firstly death ray covers only last row of the table that corresponds to one of vertices of our graph. When you are changing regular column into magic one, you are allowing death ray "go" by corresponding edge.
Now you can reformulate the statement by this way: "activate" minimal number of edges in biratrite graph, so some path of minimal lenght connects vertex of the last row of the table and vertex of the first row of the table.
You can see that required set of edges is just shortest path between these vertices. You can find this path using BFS. If BFS didn't find any path — answer is -1.
This solution works in O((n + m)2).
Author is haas.
C. Let's iterate over all spirals and chose one of them that has maximal sum of elements. Because you have O(n3) spirals, you should calculate sum of any of them in O(1). Only in this case your solution will fit into time limits.
Let's define a way for iterate over all spirals. Let's fix one of cells and then iterate over all spirals that have own center in that cell in order of increasing side. So, you can recalculate sum for every spiral from previous one in O(1) using following picture:
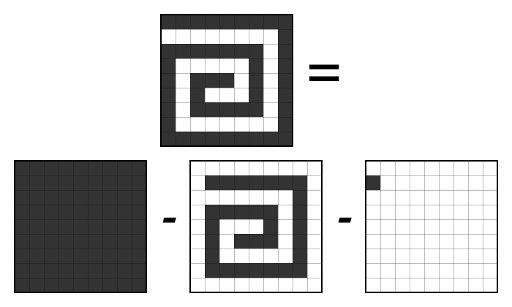
For finding the first "summand", you should in the beginning calculate rectangular partial sums.
Author is Ripatti.
D. You have bipartite graph with 3k vertices and should to color its vertices by k colors. Every color should be used exactly 3 times and there should be no edges that connect vertices at same color.
At the first, you should find both of parts of our birartite graph using, for example, DFS. Now let's consider sizes of parts.
Case 0. If both of sizes divides by 3, you can just split every of parts into groups of 3 vertices and color them.
Otherwise we can note then size of the first part is 1 modulo 3 and size of the second part is 2 modulo 3.
There are yet another 2 cases:
Case 1. You should try to find one vertex from the firts part that have 2 "antiedges" to 2 different vertices of the second part. If you found it, you should color them and reduce the problem to case 0.
Case 2. There you should try to find 2 vertices on the second part. Every of them should have 2 "antiedges" that "connect" them with 4 different vertices trom the firts part. If you found such 6 vertices, you can color them by 2 different colors and reduce the problem to case 0.
If you doesn't find coloring using this cases, answer is NO.
About implementation: it is not clear how to analyse the case 2 in acceptable time. Actually, you can find any two vertices from the second part that have at least two "antiedges". These "antiedges" will conduct to 4 different vertices of the first part because otherwise case 1 would have worked.
This solution works in O(n + m).
Author is Ripatti.
E. Let's transform all people into points on a plane with coordinates (x = ai, y = ri). What the maximal number in group of people that can be formed with some fixed leader? Answer is number of points inside rectangle (x, y): xi - k ≤ x ≤ xi + k, y ≤ yi.
Let's we allready found size of group for every person. How to find maximal group that contain points (xi, yi) and (xj, yj) both? The required group should have leader with age in range from max(xi - k, xj - k) то min(xi + k, xj + k) and responsibility at least max(yi, yj). From such leaders you should chose one that have maximal size of group. You can see that it is just query for maximum on some rectangle.
Well, let's learn to quickly find answers for queries of sums in rectangle. You should compress coordinates x ans build segment tree for sum. Then you should answer all queries in increasing order of coordinate y. When you consider some group with same y, you should initially do queries of adding values in points, and after that do sum queries on the segments from xi - k to xi + k.
Queries for maximum you can satisfy fully analogicaly using segment tree for maximum.
So, you have 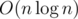 offline solution.
offline solution.
Author is havaliza.











I think that this contest was prepared badly. The point weight for task B should be 1500, it could be considered if task C is worth 1500 points too, I would vote for 1000. Because of this fault many coders didn't solve the third problem and waste a lot of time on the second one.
why does this TLE
https://codeforces.com/problemset/submission/173/213861759