628A - Tennis Tournament
The problem was suggested by unprost.
Here you can simply model the process. Or you can note that after each match some player drops out. In total n - 1 players will drop out. So the first answer is (n - 1) * (2b + 1). Obviously the second answer is np.
Complexity: O(log2n), O(logn) or O(1) depends on the realization.
628B - New Skateboard
This is one of the problems suggested by Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
The key observation is that the number is divisible by 4 if and only if its last two digits forms a number divisible by 4. So to calculate the answer at first we should count the substrings of length one. Now let's consider pairs of consecutive digits. If they forms a two digit number that is divisible by 4 we should increase the answer by the index of the right one.
Complexity: O(n).
628C - Bear and String Distance
The problem was suggested and prepared by Kamil Debowski Errichto. He also wrote the editorial.
There is no solution if the given required distance is too big. Let's think what is the maximum possible distance for the given string s. Or the more useful thing — how to construct a string s' to maximize the distance? We can treat each letter separately and replace it with the most distant letter. For example, we should replace 'c' with 'z', and we should replace 'y' with 'a'. To be more precise, for first 13 letters of the alphabet the most distant letter is 'z', and for other letters it is 'a'.
Let's solve a problem now. We can iterate over letters and greedily change them. A word "greedily" means when changing a letter we don't care about the next letters. We generally want to choose distant letters, because we may not find a solution otherwise. For each letter si we change it into the most distant letter, unless the total distance would be too big. As we change letters, we should decrease the remaining required distance. So, for each letter si consider only letters not exceeding the remaining distance, and among them choose the most distant one. If you don't see how to implement it, refer to my C++ solution with comments.
Complexity: O(n).
628D - Magic Numbers
Kareem Mohamed Kareem_Mohamed suggested the simpler version of the problem.
Denote the answer to the problem f(a, b). Note that f(a, b) = f(0, b) - f(0, a - 1) or what is the same f(a, b) = f(0, b) - f(0, a) + g(a), where g(a) equals to one if a is a magic number, otherwise g(a) equals to zero. Let's solve the problem for the segment [0, n].
Here is described the standard technique for this kind of problems, sometimes it is called 'dynamic programming by digits'. It can be realized in a two ways. The first way is to iterate over the length of the common prefix with number n. Next digit should be less than corresponding digit in n and other digits can be arbitrary. Below is the description of the second approach.
Let zijk be the number of magic prefixes of length i with remainder j modulo m. If k = 0 than the prefix should be less than the corresponding prefix in n and if k = 1 than the prefix should be equal to the prefix of n (it can not be greater). Let's do 'forward dynamic programming'. Let's iterate over digit 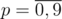 in position i. We should check that if the position is even than p should be equal to d, otherwise it cannot be equal to d. Also we should check for k = 1 p should be not greater than corresponding digit in n. Now let's see what will be the next state. Of course i' = i + 1. By Horner scheme j' = (10j + p) mod m. Easy to see that
in position i. We should check that if the position is even than p should be equal to d, otherwise it cannot be equal to d. Also we should check for k = 1 p should be not greater than corresponding digit in n. Now let's see what will be the next state. Of course i' = i + 1. By Horner scheme j' = (10j + p) mod m. Easy to see that 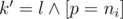 . To update the next state we should increase it: zi'j'k' + = zijk. Of course all calculations should be done modulo 109 + 7.
. To update the next state we should increase it: zi'j'k' + = zijk. Of course all calculations should be done modulo 109 + 7.
Complexity: O(nm).
628E - Zbazi in Zeydabad
The problem was suggested by Ali Ahmadi Kuzey.
Let's precalculate the values zlij, zrij, zldij — the maximal number of letters 'z' to the left, to the right and to the left-down from the position (i, j). It's easy to do in O(nm) time. Let's fix some cell (i, j). Consider the value c = min(zlij, zldij). It's the maximum size of the square with upper right ceil in (i, j). But the number of z-patterns can be less than c. Consider some cell (x, y) diagonally down-left from (i, j) on the distance no more than c. The cells (i, j) and (x, y) forms z-pattern if y + zrxy > j.
Let's maintain some data structure for each antidiagonal (it can be described by formula x + y) that can increment in a point and take the sum on a segment (Fenwick tree will be the best choice for that). Let's iterate over columns j from the right to the left and process the events: we have some cell (x, y) for which y + zrxy - 1 = j. In that case we should increment the position y in the tree number x + y by one. Now we should iterate over the cells (x, y) in the current column and add to the answer the value of the sum on the segment from j - c + 1 to j in the tree number i + j .
Complexity: O(nmlogm).
628F - Bear and Fair Set
The problem was suggested and prepared by Kamil Debowski Errichto. He also wrote the editorial.
At the beginning, to make things simpler, we should add a query (hint) with upTo = b, quantity = n, and then sort queries by upTo. Sorted queries (hints) divide interval [1, b] into q disjoint intervals. For each interval we know how many elements should be there.
Let's build a graph and find a max flow there. The answer is "YES" only if the flow is n.
- The first group A contains 5 vertices, representing possible remainders.
- The second group B contains q vertices, representing intervals.
Each vertex from A should be connected with the source by an edge with capacity n / 5. Each vertex from B should be connected with the sink by an edge with capacity equal to the size of the interval. Between each vertex x from A and y from B should be an edge with capacity equal to the number of numbers in the interval y, giving remainder x when divided by 5.
You can also use see that it's similar to finding matching. In fact, we can use the Hall's marriage theorem. For each of 25 sets of vertices from A (sets of remainders) iterate over intervals and count how many numbers we can take from [1, b] with remainders from the fixed set of remainders.
The implementation with the Hall's theorem: C++ solution.
Complexity: O(2Cn). In our problem C = 5.











Thank you for fast editorial.
Extra challenge for 628C - Bear and String Distance — can you find the lexicographically smallest answer?
Try to replace all character with smaller ones. If k > 0 in the end, start from the end, and if bigger si makes k smaller, we will replace it and so on. If k equals 0, answer is this, else answer is - 1.
Congratulations! It's correct if by "smaller ones" you mean letter 'a'.
So problem F wasn't about flows. Can anyone hack flow solutions? I'm not sure if it's possible because the graph is special.
I'm also waiting for the hacks against flows.
It seems that it is impossible to hack even naive flows. Burunduk1 suggested two tests where flow solutions works in O(b2) time (and he says that it's a maximum time we can get here), but it's not enough. If we set the constraints b ≤ 2·105 then it'll be possible to hack flow solutions.
Why n was so small in F? I spent a lot of time trying to find alternative solution because this time complexity looked too good to be true. Luckily, I was able to prove the algorithm, shrugged and got OK 5 minutes before the end of the contest.
We was discussed for a long time with Errichto the constraints. And finally we decided to make it smaller because with small C it's harder to come up with solution.
I don't get it. You tried to make problem harder by reducing n (and making the best solution looking too fast) or easier by allowing flow solutions?
PS. It was quite unexpected to end up in the first place. I should thank participants who hacked everyone above me.
On my mind with constraint C = 5 it's harder to come up with solution. The small constraints for the n, b are our fault, we should make it 5·105 and then we could hack all flow solutions (except maybe Dinic solutions). P.S.: Congrats with the first win!
in ques E what does this do?
for ( ; i < m; i |= i + 1) t[i] += v;
https://en.wikipedia.org/wiki/Fenwick_tree
what kind of bit is this ? can you explain the bit ? this is the sum function : for ( ; i >= 0; i = (i & (i + 1)) — 1) ans += t[i];
noone know how it works. it's just magic)
The key thing here is the
+ 1part. Why do we need adding1at all?Well, let's look at the binary representation of some number
x = ...01111.Now, let's add
1to the numberxand see howx + 1looks like:...01111 + 1 =...10000The
x + 1has lost all it's ones at it's end!Whatever the
xnumber is, we know that it has exactly 4 consecutive ones at it's end. If we add1to that number, the last group of 4 consecutive ones will change to zeros.If the number
xhas0as it's last digit, the change after adding1will be not as dramatic :)...01110 + 1 =...01111Notice, that in this case
xandx + 1differ only in a single digit.For problem B, I saw some solutions whereby people constructed the 2 digit numbers by the following way: num = str[i]*10+str[i+1]
Although, it should have been: num = ( str[i] — 48 ) * 10 + ( str[i+1] — 48 )
I have no idea as to why is the former still working (passing the pretests) ?
Because 48 % 4 == 0 (coincidence)
in D why the answer for this test 43 3 587 850
is 1 ????? what is the number which is multiple of 43 and 3-magic??? where am I wrong???
731
oooh, thanks, I mis-write the number on the calculator. I thought I misunderstood the problem.
In problem D, how is next next dp state calculated? I'm not able to get it. Also why are we having k = {0, 1} as third dimension in our dp. Why was there a need to introduce it in the dp?
In Problem D, How to solve f(0, a)? It may contain leading zero when len(i) < len(a). I know in the problem len(a) == len(b), so we don't care about such case. But I just wonder how to calculate the value of f(0, a).
In E, is y-axis directed down-to-up? Otherwise y + zrxy > j will always hold..
Also, do I understand correctly, that we can't "precompute" the whole Fenwick tree (for each diagonal of course) and only then make the queries? Otherwise we could go with simple prefix sums. I think this "dynamicness" makes it harder to come up with the solution.
Finally got it. The keyword for me was "events", I didn't pay attention to it while reading the solution. Though I still don't understand the order in which the editorial's solution processes the map.
In problem F, when we are finding matching, what is mapped against what? What do you mean by 2^5 vertices?
There are 5 vertices in the first group so there are 25 sets of vertices.
I don't understand your question "what is mapped against what?", so I will just write a bit about the matching thing. We have a bipartite graph with two groups of vertices, described in the editorial. It's a problem similar to matching (or vertex cover) problem but for each vertex we have some required degree (the number of incident edges in "matching"). E.g. each of 5 vertices in the first group should be incident to n / 5 edges chosen in matching. You can think that such a fake vertex represents n / 5 real (true) vertices, all connected to the same vertices from the second group. The same applies to the second group — e.g. the interval where we want the degree 3 represents 3 real vertices. After replacing fake vertices described in the editorial with real vertices you would get a bipartite graph with exactly n vertices in each of two groups. And then we ask about the perfect matching.
Is this some other kind of hall marriage theorem? The one I knew was applying only for bipartite graphs. Indeed, you could convert some nodes as you said, but the huge problem is that we have edges between the two groups with capacities more than 1. Could you explain more thoroughly how to bring the problem to the form of a bipartite graph, maybe with some example? If we replace an interval with q nodes where q is the number of numbers we know Limak will have in that interval, then, from those nodes, exactly what edges will you draw? If you want to draw the same edges as before replacing the intervals, then you'll need capacities and it's just not right...Could you actually give an example? I find it strange that in your source you checked for something to be in an interval. The hall's theorem that I know only requires for an inequality (not two as in your case) to hold. Firstly, I really don't believe that there is any way to change the network in one with capacities of 0 or 1. Secondly, even if we did, as long as the obtained network is not bipartite (maybe tripartite?), I wouldn't know how to apply the theorem. Sorry for the question, but I already spent an hour trying to understand and didn't succeed. Hopefully, your answer could help others as well
I don't understand problem D.Why number 1 is 7-magic?Digit 7 doesn't appear in it at all.Maybe there is a bug with problem statement?Maybe there is no comma between 17 and 1?
Do you see any even position with some
digit != 7? I don't.Thanks.I get it now.
Edit:I originally thought 7 has to appear at least once on even position and not appear on any odd position.
So 7 has to appear on EVERY even position?For example 172738 is not 7-magic right?
Problem F:
i though the complexity of dinic is O(V^2*E) where V = number of Nodes and E= Number of Edges . Here V is maximum 10^4 . then how can Dinic solution pass for this problem ? Can someone tell me what i'm missing ?
Dinic algorithm complexity can be improved to O(V*E*log(V)). It is the improved version that everyone uses in the contests. Since E is only O(n) in this problem, the running time is only O(n^2*log(n)).
I read a bit more on flow algorithms and I am no longer sure what is time complexity of the standard algorithm. But in this problem the maximum flow is only O(n) with integer capacities and so all algorithms work pretty fast.
I know only complexity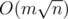 for the networks with capacities equals to 1. Complexity in general case of course O(n2m) as written above.
for the networks with capacities equals to 1. Complexity in general case of course O(n2m) as written above.
I am not able to understand the editorial of problem E.
Problem E,the last few words should be x + y? 'i' wasn't mentioned before.
can someone tell me the reason of getting even after using dp for problem D ?
Here is my Submission
Problem E can be solved without using fenwick tree, maintaining 2 pbds is a bit easier i believe as if we move along anti diagonal from the right, our requirement of one value increases and after removing all unwanted instances of it from the 1st set and from it's second mirroring one, we just need count of all elements satisfying another value range.
Can someone please help me with the D problem. I came up with a solution similar to one in the editorial. The only difference in the implementation is that in editorial forward dynamic programming is used, whereas I calcuated in bottom-up manner. I am unable to reason out, why I am getting TLE. Here is a link to my solution : https://codeforces.com/contest/628/submission/82218592
Hi, Thanks for providing solution. I think in your solution you passed string without references so, it gets created every time function calls. try to pass it by reference, it'll reduce time and you can avoid TLE.
Sorry for necroposting, could some one explain this implementation of D 16207597 dreamoon_love_AA