Hello Codeforces,
Recently I decided to start learning geometry so I found out that I have to start with the simple geometry, basic shapes, basic laws and cakewalk problems to set off my journey with geometry and computational geometry then, so I came across this problem from the gym,
Given a circle (the center of the circle |x|,|y| <= 1000, and the radius r <= 10000) .
Given a rectangle (the coordinates of the bottom-left corner and the upper-right corner, |x|,|y| <= 1000 as well) .
It's guaranteed that the upper-left corner of the rectangle is inside the circle, the width and the height of the rectangle are longer than 2.r .
you're to calculate the area of the intersection between the circle and the rectangle .
Here's what I did :
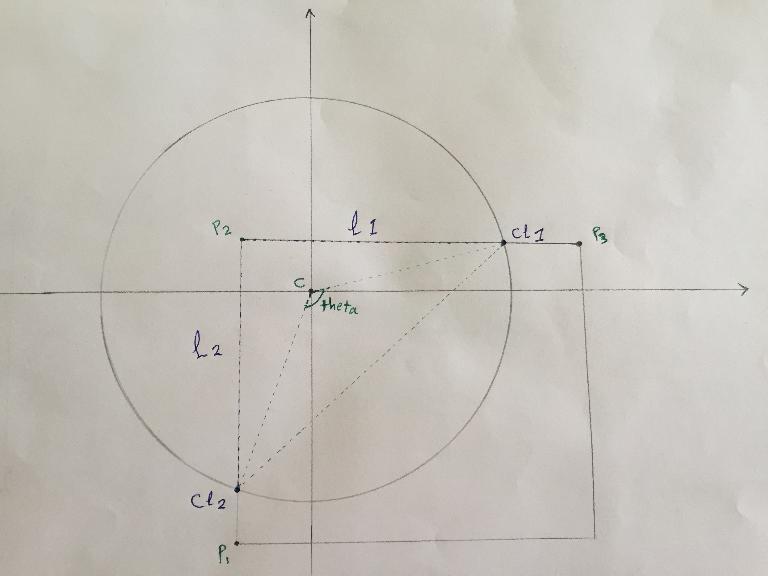
- Obtain the two lines P2-P3 let's say L1 and P2-P1 let's say L2 .
- Find the points of the intersection between the lines L1,L2 and the the circle, They're CL1, CL2 .
- Compute the angle (CL1 C CL2) theta .
- Compute the area of the circular sector determined by theta, say A .
- Subtract the area of the triangle (CL1 C CL2) from A .
- Add the area of the triangle (CL1 P2 CL2) to A and A is the answer .
So I keep getting WA for the couple past days. Since it's being the first time I write a geometry code I know it'd be so buggy and really it was, I've been debugging it for hours and I re-wrote it several times, and eventually I had no thing to do with it, I badly ran out of my shots :(
Here's my code .
It would be really appreciated if someone tells me what's going wrong (maybe it's my algorithm though, Now I doubt it's absolutely correct) Thanks in advance .
By the way, any advice, references, and problems would help a noob to kick-off in geometry would be highly appreciated as well .
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 14:18:43 (h1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I solved this using calculus (if you want another alternative).
First, translate the center of the circle to the origin. Since the integral can be interpreted as an area we are going to separate the circle in half (below the x axis and above the x axis) and get the areas from them.
A good thing to notice is that, by symmetry, if the line L1 is above the x-axis the area you're going to sum above the x-axis is the same area you would subtract if L1 was below the x-axis (for calculating the area, below of the x-axis, of the circle and subtracting that from the rectangle with rounded border).
It's really a nice approach.
I'd be so grateful if you could elaborate more on how did you come with function you integrate.
I will solve for this drawing but the other configurations are similar. The blue + white area needed are subtracted instead of added from the orange one when the rectangle doesn't have points above the x-axis.
The circle equation is just
the plus sign is for the part above the x-axis, the negative for the part below the x-axis. Find the points P1 and P2 and then integrate the circle equation from x = P1 (or P2) to x = r to get the needed white (orange) area. The blue area for the rectangle is straightforward.
To solve the integral we can make a trigonometric substitution, a possible one is x = rsin(θ) and integrate θ instead of x.
Thank you .
That was very useful and helpful
I do appreciate your help :D .
UPD(deleted): It does not refer to this problem.
The upper-left corner of his farm is inside the well.
The width and the height of the farm are bigger than Diameter (2R) of the well.
from the problem statement. I think the problem setter made these constraints to make the problem easier and evade such tricky cases, as the problem states I think it will always be just two intersection points .
Oh i missed this "rectangle are longer than 2.r"
Any other solutions beside calculus ??
move the circle to the position where its center is (0,0) and move the rectangle to the corresponding position. using atan2/atan will makes the problem easier to solve.