Edvard's blog

Editorial of Educational Codeforces Round 11
By Edvard, history, 8 years ago, translation, In English

660A - Co-prime Array

The problem was suggested by Ali Ibrahim C137.

Note that we should insert some number between any adjacent not co-prime elements. On other hand we always can insert the number 1.

С++ solution

Complexity: O(nlogn).

660B - Seating On Bus

The problem was suggested by Srikanth Bhat bharsi.

In this problem you should simply do what was written in the problem statement. There are no tricks.

C++ solution

Complexity: O(n).

660C - Hard Process

The problem was suggested by Mohammad Amin Raeisi Smaug.

Let's call the segment [l, r] good if it contains no more than k zeroes. Note if segment [l, r] is good than the segment [l + 1, r] is also good. So we can use the method of two pointers: the first pointer is l and the second is r. Let's iterate over l from the left to the right and move r while we can (to do that we should simply maintain the number of zeroes in the current segment).

C++ solution

Complexity: O(n).

660D - Number of Parallelograms

The problem was suggested by Sadegh Mahdavi smahdavi4.

It's known that the diagonals of a parallelogram split each other in the middle. Let's iterate over the pairs of points a, b and consider the middle of the segment 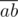: 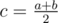. Let's calculate the value cntc for each middle. cntc is the number of segments a, b with the middle c. Easy to see that the answer is .

C++ solution

Complexity: O(n2logn).

660E - Different Subsets For All Tuples

The problem was suggested by Lewin Gan Lewin.

Let's consider some subsequence with the length k > 0 (the empty subsequences we will count separately by adding the valye mn at the end) and count the number of sequences that contains it. We should do that accurately to not count the same sequence multiple times. Let x1, x2, ..., xk be the fixed subsequence. In the original sequence before the element x1 can be some other elements, but none of them can be equal to x1 (because we want to count the subsequence exactly one time). So we have m - 1 variants for each of the elements before x1. Similarly between elements x1 and x2 can be other elements and we have m - 1 choices for each of them. And so on. After the element xk can be some elements (suppose there are j such elements) with no additional constraints (so we have m choices for each of them). We fixed the number of elements at the end j, so we should distribute n - k - j numbers between numbers before x1, between x1 and x2, \ldots, between xk - 1 and xk. Easy to see that we have 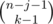choices to do that (it's simply binomial coefficient with allowed repititions). The number of sequences x1, x2, ..., xk equals to mk. So the answer is . Easy to transform the last sum to the sum 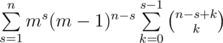. Note the last inner sum can be calculating using the formula for parallel summing: 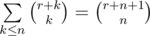. So the answer equals to 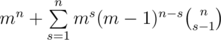. Also we can get the closed formula for the last sum to get logarithmic solution, but it is not required in the problem.

C++ solution

Complexity: O((n + m)log MOD), где MOD = 109 + 7.

660F - Bear and Bowling 4

The problem was prepared by Kamil Debowski Errichto. The problem analysis is also prepared by him.

The key is to use divide and conquer. We need a recursive function f(left, right) that runs f(left, mid) and f(mid+1, right) (where mid = (left + right) / 2) and also considers all intervals going through mid. We will eventually need a convex hull of lines (linear functions) and let's see how to achieve it.

For variables L, R (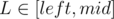, 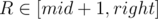) we will try to write the score of interval [L, R] as a linear function. It would be good to get something close to aL·xR + bL where aL and bL depend on L, and xR depends on R only.

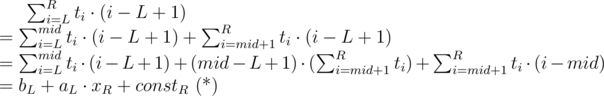
For each L we should find a linear function fL(x) = aL·x + bL where aL, bL should fit the equation ( * ):

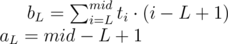
Now we have a set of linear functions representing all possible left endpoints L. For each right endpoint R we should find xR and constR to fit equation ( * ) again. With value of xR we can iterate over functions fL to find the one maximizing value of bL + aL·xR. And (still for fixed R) we should add constR to get the maximum possible score of interval ending in R.

Brute Force with functions

Now let's make it faster. After finding a set of linear functions fL we should build a convex hull of them (note that they're already sorted by slope). To achieve it we need something to compare 3 functions and decide whether one of them is unnecessary because it's always below one of other two functions. Note that in standard convex hull of points you also need something similar (but for 3 points). Below you can find an almost-fast-enough solution with a useful function bool is_middle_needed(f1, f2, f3). You may check that numbers calculated there do fit in long long.

Almost fast enough

Finally, one last thing is needed to make it faster than O(n2). We should use the fact that we have built a convex hull of functions (lines). For each R you should binary search optimal function. Alternatively, you can sort pairs (xR, constR) and then use the two pointers method — check the implementation in my solution below. It gives complexity 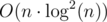because we sort by xR inside of a recursive function. I think it's possible to get rid of this by sorting prefixes 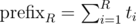in advance because it's equivalent to sorting by xR. And we should use the already known order when we run a recursive function for smaller intervals. So, I think is possible this way — anybody implemented it?

Intended solution with two pointers

Complexity: O(nlog2n).

  • Vote: I like it
  • +32
  • Vote: I do not like it

Comments Comments (43)
| Write comment?
»
8 years ago, # |
← Rev. 3   Vote: I like it +26 Vote: I do not like it

We don't need divide and conquer in F. We can use only convex hull trick. This way the solution has better complexity and is easier to implement.

Let's say that S1 is a normal prefix sum array, that is S1[i]=A[1]+A[2]+...+A[i] and S2 is again a prefix sum array but this time every element is multiplied by its index, that is S2[i]=A[1]+2*A[2]+3*A[3]+...+i*A[i]. Let's choose some R which will be the right end of our chosen interval. Now we are looking for the L that minimizes S2[R]-S2[L-1]-(L-1)*(S1[R]-S1[L-1]) which is a standard use of CHT — http://codeforces.com/contest/660/submission/17245184.

The complexity is O(NlogN).

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Nice! And is it possible to implement it with integers only?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Ah yes, since we need to compare A1/B1 and A2/B2 where A1, B1, A2 and B2 are integers. Thanks if you asked to make me think about it, I will know that in future! :)

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 3   Vote: I like it +6 Vote: I do not like it

        But I think your B may be up to N2·107 and A is up to N·107 so long long's won't be enough to multiply them. So maybe the intended solution was valuable anyway because it allowed to use integers only.

        → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it 
sum_so_far += t[i];
score_so_far += sum_so_far;
Fun f = Fun{mid - i + 1, score_so_far};

sum_so_far can be N * 107

score_so_far can be N2 * 107

When we will calculate f.a*f.b it can be N3 * 107, which is bigger than 1022.

Am I missing something?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    f.a is up to N and f.b is up to N2·107 but we don't multiply some random values. Values of f.a increase by 1 and values of f.b increase by N·107, as we move from fi to fi + 1 (and we multiply differences like f1.a - f2.a). I came up with a proof that it amortizes but I don't see that proof right now. I will try to get it again (and I hope it exists).

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My approach for Problem F is as follow (It didn't work, but I can't find the bug in this algorithm):

We can determine the stop point (deleted suffix) by looping back from n to 1:

for(int i=n; i>=1; i--) {
        sum += ts + a[i], ts+=a[i];
        if (sum < 0) {
            sum=0, ts=0;
            if(a[i] < 0) 
                bef[i-1]=1;
            else 
                bef[i]=1;
        }
    }

then I implemented this for loop to get the best stop point for every i:

bef[n]=1;
    int last = 1; 
    for(int i=1; i<=n; i++) {
        if(bef[i]) {
            for(int j=last; j<=i; j++) go[j] = i; 
            last = i+1; 
        }
    }

So now go[i]+1---> n will be the deleted suffix for item i.

I think if this part of code works , I think this problem can be solved in O(n) Complexity, And if it doesn't work, my approach will fail entirely.

So, what is wrong with my code?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In C problem, why complexity O(n + k)? even if k > n it will be O(n).

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Well technically you are right.

    Anyway considering the fact, that (by the statement) K<=N, then O(n+k) == O(n) (the complexities are equal)

    So → you are right, but so is Edvard (at least in asymptote) ^_^

    But I agree that it might be slightly misleading, considering, that the "k" really does not have to be used for counting of the complexity :)

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks. Fixed.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For D, another interpretation is to count pairs (dx, dy) for all pairs of points and then for each such pair add to answer count * (count - 1) / 2. Since the parallel sides are parallel and has same length. But we will count each parallelogram twice, so divide the answer by 2.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    It's just a building vectors on each parallelogram's side, isn't it?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      an easier aproach and easy to implement is to find miidle of each line then use the fact that in every parallogram diagonals intersect at the middle.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It will be not working if more than 3 points can lie on the same line. For example, {(2,2),(4,4),(-2,-2),(-4,-4)} is not a parallelogram. Yes, I know, following by problem statement it`s impossible, but the fact remains.

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      exactly as you say!

      Build vectors, merge them (count number of same vectors) and use Gauss's formula!

      ^_^

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How can you solve Problem E?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I could not understand the editorial. Can someone please explain?

    → Reply
»
8 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Out of A,B,C,D guess which one I found the hardest? That's right! A. FML ;_;

→ Reply
»
8 years ago, # |
  Vote: I like it -8 Vote: I do not like it

There is another method of solving B with sorting. Some people might find it easier and shorter to code

17235532

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For Problem F you can just make a form of slope such that (p[j] — p[k]) / (j — k) <= s[i], where p[i] = i * sigma(a[i]) — sigma(i * a[i]), s[i] = sigma(a[i]). then you can make a convex hull, for each i, you just to use binary search to find the best choice and update the answer. this complexity is O(nlogn)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

for E ,in 5th line ,there should be m - 1 choices for each of them but not k-1 choices.

→ Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it -36 Vote: I do not like it

Here's just a funny story I want to tell you guys.

I solved problem F by a weird O(N) algorithm, which is not correct.

http://codeforces.com/contest/660/submission/17264773 (Accepted)

Maybe test cases are weak, so my solution passed 52/54 tests (failed on 2 tests, I had to write "if n=... cout..." in order to AC). Seem crazy right ?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

An O(n) alternative for E:

    LL powr = 1;
    LL current = 1;

    ii (n) {
        current = ((2*m)*current - (current - powr)) % MOD;
        powr = (powr * m) % MOD;
    }

    cout << current << '\n';

This is more direct from the statement of the problem. We build the set of all sequences, element by element, from left to right, and current tracks the count of distinct subsequences within all the sequences (visualise a different room for each sequence maybe). At each step for each room we create m new rooms. Also, in each room, each subsequence splits into two: one with the newly added element, and one without. Except we have just created some subsequences that were already there; all of them, in fact (except the empty ones), so we subtract them (the number of empty ones is powr, which is m**i).

Seems to work: 17242031.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    It seems I forgot how to solve recurrences. But Wolfram Alpha hasn't. Edit: for some reason that link doesn't work. Here it is: https://www.wolframalpha.com/input/?i=solve+recurrence+a%5Bi%5D+%3D+a%5Bi-1%5D*K+%2B+M%5E%28i-1%29

    So there's a O(lg (n+m+MOD)) solution. Logarithmic time means we can solve it in Python!

    Complete solution:

        import sys
    n, m = map(int, sys.stdin.readline().split())
    MOD = int(1e9+7)

    first_term = pow(2*m-1, n, MOD)
    rr = first_term + ( first_term - pow(m, n, MOD) ) * pow(m-1, MOD-2, MOD)

    print rr % MOD if m > 1 else n+1

    Apparently it works: 17273456

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hey,this may be a bit naive question but please can you explain how the answer for n=2 & m=2 for this problem is 14.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      There are 4 sequences and in each we need to count unique subsequences:

      00: [], [0], [0,0]

      01: [], [0], [1], [0,1]

      10: [], [0], [1], [1,0]

      11: [], [1], [1,1]

      That's 3+4+4+3.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For B, you say "There are no tricks." What about 17246985?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I don't understand why the problem D is complexity O(n^2*logn), I know that the n^2 is there because we have to compare every segment with every other segment but I don't understand why the log(n).

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The log(n) comes up from the complexity of the data structure needed to handle cnt, such as a C++ map. Note that you need to count how many times a point appears as a middle point.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I didnt understand the samples in the question for E, could someone help me out here?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can someone elaborate on the following from problem E's editorial?

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    +1

    → Reply
  • »
    »
    3 years ago, # ^ |
    ← Rev. 6   Vote: I like it +9 Vote: I do not like it

    4 years later, you finally get your answer! :D

    Claim 1:

    $$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{k = 0}^{s - 1}{n - s + k \choose k}}$$$

    Proof:

    We have:

    $$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{k = 1}^{n}{\sum_{j = 0}^{n - k}{m^{k + j}(m - 1)^{n - (k + j)}{n - j - 1 \choose k - 1}}}$$$

    Observe that the quantity $$$k + j$$$ appears in most of the members of the inner multiplication, so summing over it in the outer sigma would simply the sum. Let $$$s = j + k$$$. Instead of summing over $$$k$$$ in the outer and $$$j$$$ in the inner, let's sum over all of the values of $$$s$$$ in the outer and $$$j$$$ in the inner, and the corresponding value of $$$k$$$ will be $$$s - j$$$.

    This is useful because $$$m^{k + j}(m-1)^{n - (k + j)}$$$ will turn into $$$m^{s}(m - 1)^{n - s}$$$ and we can take that quantity outside of the inner sum because it's independent of $$$j$$$. Also, note that the minimum value for $$$s$$$ is $$$1 + 0 = 1$$$, and the maximum value for $$$s$$$ is simply $$$n$$$. Finally, note that when fixing $$$s$$$, $$$j$$$'s possible range is $$$[0, s - 1]$$$, as $$$k$$$'s possible range is $$$[1, s]$$$ and $$$j = s - k$$$.

    So we get: $$$\sum_{k = 1}^{n}{\sum_{j = 0}^{n - k}{m^{k + j}(m - 1)^{n - (k + j)}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{\sum_{j = 0}^{s - 1}{m^s(m - 1)^{n - s}{n - j - 1 \choose s - j - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1}}$$$

    Now we have to deal with the inner creature, $$$\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1}$$$. Let $$$k$$$ (note that this is NOT the $$$k$$$ from before, this is simply bad variable name choice) be $$$s - j - 1$$$. we want to sum over all values of this $$$k$$$ instead all values of $$$j$$$. obsevre that based on the definition we gave for $$$k$$$, $$$j = s - k - 1$$$, and because the range for $$$j$$$ is $$$[0, s - 1]$$$, the range for $$$k$$$ will be $$$[0, s-1]$$$ (because when $$$j$$$ is $$$0$$$ $$$k$$$ will be $$$s - 1$$$ and when $$$j$$$ is $$$s - 1$$$, $$$k$$$ will be $$$0$$$ (we did a similar thing when converting to summing over $$$s$$$)).

    We get: $$$\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1} = \sum_{k = 0}^{s - 1}{n - (s - k - 1) - 1 \choose k} = \sum_{k = 0}^{s - 1}{n - s + k \choose k}$$$

    Finally, substituting and combining everything: $$$\sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{j = 0}^{s - 1}{n - j - 1 \choose s - j - 1}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{k = 0}^{s - 1}{n - s + k \choose k}}$$$.

    To conclude, coming back to the initial equality we found: $$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}\sum_{k = 0}^{s - 1}{n - s + k \choose k}}$$$, as desired. $$$\blacksquare$$$

    Claim 2:

    $$$\sum_{k = 0}^{s - 1}{n - s + k \choose k} = {n \choose s-1}$$$

    Proof:

    Introducing: The Hockey-Stick Identity

    Our intuition is to use the Hockey-Stick Identity. The Mirror-Image Hockey-Stick Identity is stated as follows (specifically MHS & RHS of it in Wikipedia): $$$\sum_{k = 0}^{n - r}{k + r \choose k} = {n+1 \choose n-r}$$$ (note that $$$n \ge r$$$ must be satisfied).

    We have $$$k$$$ in the bottom part of the choose, so the thing added to it, $$$r$$$, should be the upper part of the choose in the summation minus $$$k$$$, namely, let $$$r = n - s$$$. also, let the $$$n$$$ from the Hockey-Stick identity $$$n - 1$$$ (where this $$$n$$$ is the length of the sequence). Note that $$$n - 1 \ge n - s$$$ therefore the $$$n \ge r$$$ condition is satisfied.

    Substituting: (HockeyStick($$$r = n - s$$$, $$$n = n - 1$$$))

    $$$\sum_{k = 0}^{n - 1 - (n - s)}{k + n - s \choose k} = {n - 1 + 1 \choose n - 1 - (n - s)} \implies \sum_{k = 0}^{s - 1}{n - s + k \choose k} = {n \choose s-1}$$$, as desired. $$$\blacksquare$$$

    Substituting into Claim 1:

    $$$\sum_{k=1}^{n}{\sum_{j = 0}^{n - k}{m^km^j(m - 1)^{n - j - k}{n - j - 1 \choose k - 1}}} = \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}{n \choose s-1}}$$$

    And now, the only thing left is to include the empty sequence, we should count every sequence of length $$$n$$$, and there are $$$m$$$ options for each position therefore $$$m^n$$$ such sequences therefore we arrive at our final answer:

    $$$m^n + \sum_{s = 1}^{n}{m^s(m - 1)^{n - s}{n \choose s-1}}$$$ $$$\square$$$

    → Reply
    • »
      »
      »
      3 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      I will need to go back to this problem again lol. Thanks for writing this down!

      → Reply
      • »
        »
        »
        »
        3 years ago, # ^ |
        ← Rev. 2   Vote: I like it +3 Vote: I do not like it

        You're welcome! :)

        Once you finish reading & upsolving, please update here, I wrote this explanation in 2 AM and error checking would be cool :p

        → Reply
»
5 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

The closed formula being referred to in problem E is:

$$$ans = m^n + \frac{m}{m-1}((2m-1)^n - m^n)$$$.

It doesn't work when $$$m = 1$$$ (because of division by 0). But in that case, since there is only a single sequence of length $$$n$$$ comprising of all $$$1$$$-s, the answer is simply $$$(n + 1)$$$.

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

A note for Problem E: Different Subsets For All Tuples

What got me stuck on the problem is that I initially considered the sequence x1, x2 .. xk but I said xi cant appear in the range (position of xi-1, position of xi+1), but that completely ignored cases in which the value appears multiple times in the same segment.

So usually, in combinatorics we like to rephrase things and identify things, so the idea for cases in which the sequence appears multiple times is to only consider the sequence with the smallest lexicographical position vector. this is what allows for the described approach.

→ Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Since math is hard, I have a solution for $$$E$$$ which requires basically no math and is really easy to implement! I can't prove the correctness of it in any nice way.

So first is to try out small $$$(n, m)$$$ and brute force the answers, probably using some computer program or something. That way, we can try to find a pattern.

Code

If you put this in a table, we get:

2 4 6 8 10 12

3 14 33 60 95 138

4 46 174 436 880 1554

5 146 897 3116 8045 17310

6 454 4566 22068 73030 191706

I index the table such that the column index represents $$$m$$$ and the row index represent $$$n$$$.

Let's read the table column by column. The third column is:

6 33 174 897 4566

Notice that everything seems to be around $$$5$$$ times bigger than the previous number. There's a little bit of an offset, though. The offsets are powers of $$$3$$$.

The fourth column:

8 60 436 3116 22068

Notice that everything seems to be around $$$7$$$ times bigger than the previous number. There's a bit of an offset, by powers of $$$4$$$.

And that's the main observation.

$$$\boxed{f(n, m) = f(n - 1, m) \cdot (2 \cdot m + 1) + m^{n - 1}}.$$$

Easy to constructive recursive solution from there.

→ Reply
»
2 years ago, # |
  Vote: I like it +3 Vote: I do not like it

DP solution for Problem E:

For a specific sequence $$$a_1, a_2, a_3, ... $$$, it's known that $$$dp[i] = dp[i-1] * 2 - dp[j-1]$$$ in which $$$j$$$ is the latest position that $$$a_j = a_i$$$.

Now, let $$$dp[i]$$$ represent the sum of $$$dp[i]$$$ sequence whose last element is specific $$$x$$$. $$$x$$$ may be any number between $$$1$$$ to $$$m$$$, but it doesn't matter. $$$dp[i] = dp[i-1] * m * 2$$$ is hold for every sequence. And we should subject some $$$dp[j]$$$ from it. We can iterator the latest $$$j$$$, count the number, so we can get:

$$$dp[i] = dp[i-1] * 2 - \sum_j dp[j-1] * m * {(m-1)}^{i-j-1} $$$

And the sum is very easy to maintain when we loop it.

146751249

→ Reply
»
22 months ago, # |
  Vote: I like it -10 Vote: I do not like it

Here's insight into "parallel summing" in problem e solution: https://codeforces.com/blog/entry/104172

→ Reply