Hi everyone!
I'd like to invite you to participate in April Clash on HackerEarth. Contest is scheduled on April, 16. Contest duration is 24 hours, so we hope it will be possible to find comfortable time for everyone in any timezone :) Check your time.
There will be six tasks in a problemset. Five of them are standard algorithmic problems with partial solutions allowed — you get points for every test that your solution passed. And the last task is an approximate problem — your score for this task depends on how good your solution is comparing to current best solution.
kostya_by is author of this problemset. Check out his problems on Codechef and Hackereath to make sure that he is able to provide good problems :)
As you might guess I worked on this contest as a tester and that was nice:) In our opinion several tasks will be not too hard for beginners (don't give up and show your best with partial scoring — even very naive solution may give you some points; and 24 hours should be enough for you to read all problems and find some tasks which you can solve).
At the same time we are pretty sure that some tasks will be decent challenges for experienced contestants too. But if you think that classic part of problemset is easy — the approximate problem is waiting for you :)
Also we want to thank belowthebelt for handling all technical aspects of contest preparation.
The problem statements will be provided in English and Russian.
As usual, here is one more reason for you to participate in this contest:
Top5 of leaderboard will grab some nice prizes:
$100 Amazon gift card + HackerEarth T-shirt
$80 Amazon gift card + HackerEarth T-shirt
$50 Amazon gift card + HackerEarth T-shirt
HackerEarth T-shirt
HackerEarth T-shirt
Good luck to everybody — let's have fun :)











In the hackerearth link, the start time is provided as 2.30 am CDT which is 3.30 EDT.
In your link, you have provided the time as 2.30 EDT instead of 2.30 CDT (which is 1.30 CDT).
When I click on add to Google calendar link in the page, it tries to add an event with start time 1.30am EDT (which is 12.30pm CDT).
Can you confirm on the actual start time?
The contest starts in an hour. Good luck, everyone!
In the contest description is written, that there will 3 approximate and 3 algorithmic challenges.
Wait, what? Where? It's standard. 5 algorithmic, 1 approximate.
Two algorithmic problems require custom checkers and making them approximate is the only way to handle that.
How was the contest, guys? Which was your favorite problem? And, what were your approaches for the approximate problem? :)
Do you even easy problems bro? Nice one. In terms of difficulty, this is exactly what I want from a 24-hour contest. I wish I had more time to solve problems.
My comment on problems:
Money Change: I overlooked the constraint k ≤ 10 for an hour. Reducing the complexity to O * (3k) is straight forward but I think we can reduce the complexity to O * (2k) via fast convolutions.
Choosy Bride: I couldn't figure out the segment tree solution that using a segment tree but I wrote a square root decomposition solution instead which surprisingly runs faster enough. The segment tree solution is an interesting technique indeed.
Birthday Party: I firstly note that the triplet condition is the same as saying that the points on a plane are colinear. If I fix two points then you can greedily choose the maximal set of points. Because of the condition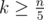 , The probability of choosing right pair is at least
, The probability of choosing right pair is at least 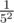 when you choose a pair of points randomly. Can we solve this problem when there is no restriction on k? I think not. Because it contains a problem which is 3SUM-Hard.
when you choose a pair of points randomly. Can we solve this problem when there is no restriction on k? I think not. Because it contains a problem which is 3SUM-Hard.
Maximal Cactus: Prove that you can add exactly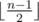 for a tree of n nodes. The rest is relatively straightforward and mostly a matter of an implementation.
for a tree of n nodes. The rest is relatively straightforward and mostly a matter of an implementation.
Compact Tree on a Table: My approach to this problem is a simple greedy strategy. I did a breadth first search from several random root points.
Congratulations to Top 5!
eatmore
anta
akashdeep
yarrr
zeliboba
We remind that contests are individual and any kind of collegiate participation is forbidden, cheaters will be disqualified.
Editorials and submissions have been published.
Alternate approach for Birthday Party with a better probability:
1) Instead of choosing a pair of points, choose any one random point.
2) There is a k / n probability that it belongs to a an optimal subset (provided one exists).
3) Now make this as origin, and find the slopes of the other points, and choose the most frequent slope. If this frequency exceeds k — 1, you have found your answer. Else, repeat from step 1.
Probability of success over m iterations now becomes 1 — (1 — (k / n)) m instead of 1 — (1 — (k / n)2) m
Deterministic solution for problem D (Birthday Party):
Separate the input points into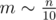 buckets of roughly equal size. For each pair of points within the same bucket, find the line that passes through them (there would be about 5n such pairs). It can be shown that a if a line passes through at least k points, it will pass through at least k - m such pairs. So, find all the lines that pass through at least k - m pairs and check them.
buckets of roughly equal size. For each pair of points within the same bucket, find the line that passes through them (there would be about 5n such pairs). It can be shown that a if a line passes through at least k points, it will pass through at least k - m such pairs. So, find all the lines that pass through at least k - m pairs and check them.